导读：欢迎来到 StarRocks 源码解析系列文章，我们将为你全方位揭晓 StarRocks 背后的技术原理和实践细节，助你逐步了解这款明星开源数据库产品。本期 StarRocks 技术内幕将介绍 Join Reorder 算法如何找到最优解的原理。

背景介绍

多表 Join 是现实业务场景中很常见的需求，其执行效率和 Join 的执行顺序息息相关，比如两表 t1 Join t2 就有 t1 ⨝ t2 和 t2 ⨝ t1 两种方式（Join 满足交换律），三表 t1 Join t2 Join t3 由于 Join 满足结合律，可以 t1 和 t2 先做Join，再和 t3 Join，即(t1 ⨝ t2) ⨝ t3，也可以先做 t2 和 t3 的 Join，再和 t1 做 Join，即 t1 ⨝ (t2 ⨝ t3)。

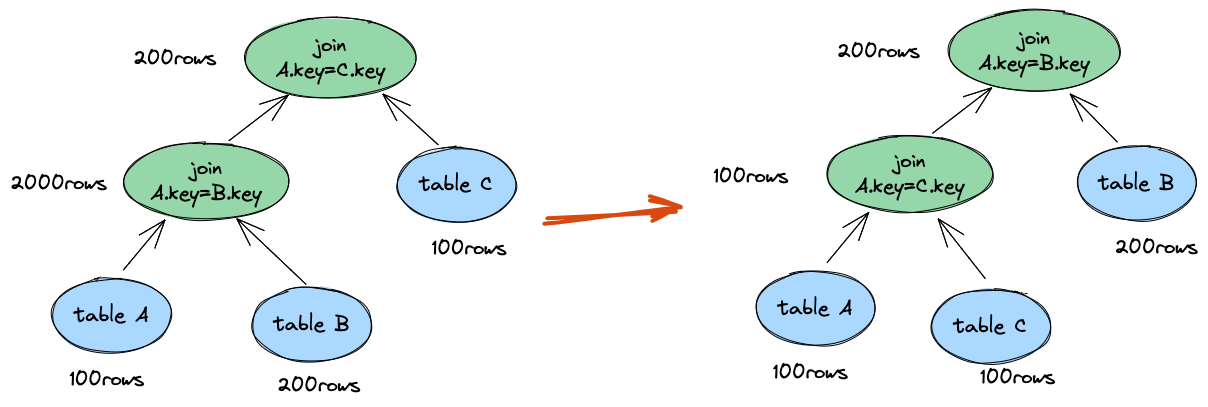
如上图所示，Table A 和 B 的 Join 会生成较大的 Join 中间结果集，使用 Join Reorder 算法优化后，结果集缩小显著。Join 的执行顺序和执行方式对查询性能的结果影响非常明显，部分场景下甚至能带来数量级的差异，因此优化器选择出好的 Join 顺序尤为重要。

整体流程

刚才提到 Join 是满足交换和结合律的，因此通过 Join 的交换结合，可以拓展出所有的 Join 顺序。在 “StarRocks 优化器代码导读”中我们介绍过，StarRocks 优化器使用 Memo 进行空间搜索，通过使用 transform rule 来完成 GroupExpression 的转换，使用 JoinCommutativity 和 JoinAssociativity 两个 rule 完成 Join 的交换和结合。先来看张图，可以帮助你理解：

上图罗列了三表 A、B、C 所有可能的 Join 顺序，这些在 Memo 中表示成不同的 GroupExpression，并记录在同一个 Group 中。注意，这些 Join 顺序不同的 GroupExpression 是逻辑等价的。

理论上我们可以使用 Join 的交换结合枚举出所有的 Plan，通过计算每个 Plan 的 Cost，从而选出代价最小的 Plan。但实际上随着 Join 节点的增多，优化器的搜索空间会成指数级放大。如下图所示：

随着 Join 节点的增多，优化器将无法枚举出所有 Plan。另一方面，优化器需要在有限时间内给出最优解，因此我们需要使用高效的 Join Reorder 算法来决定 Join 的顺序。在无法枚举所有的 Join 顺序时，StarRocks 使用了贪心和动态规划两种算法来决定多表 Join 的顺序，具体策略是：

Plan 中 Join 节点小于等于 4（可通过 session 变量 cbo_max_reorder_node_use_exhaustive 修改）个时，使用枚举的方法决定Join顺序。
Plan 中 Join 节点大于 4，小于等于 10（可通过 session 变量 cbo_max_reorder_node_use_dp 修改）个 Join 节点时，使用动态规划和贪心算法决定 Join 顺序。
Plan中 Join 节点大于 10个的时候，使用贪心算法决定 Join 的顺序。
如果 Plan 中的 Scan 节点包含未知的列统计信息，将只生成默认的左深树。

枚举的方法可以通过 Cascades 框架估算出分布式计划的代价，DP 和贪心算法生成的 Plan 则需要通过 Memo 的 Property Enforce 实现，因此所有通过贪心和 DP 生成的 Plan Tree 都需要 Copy In Memo，参与后续搜索空间的拓展并计算分布式 Plan 的 Cost。

DP 和贪心算法选择出的 Join Order 是单机最优 Plan，为了尽量找到最优的分布式 Plan，StarRocks 在Join 个数不超过cbo_max_reorder_node_use_dp 时，会同时保留 DP 和贪心的 Plan，且贪心算法也会保留 Cost 最小的 10 个 Plan，为后续找到“最优”分布式 Plan 提供更多的可能性。接下来，我们将详细介绍相关代码。

代码导读

Join 交换结合

Join 的交换和结合律的使用，是基于 Cascades 优化框架实现的，因此在 StarRocks 中只需要实现对应的 Transform Rule，就可以完成 Join 的交换和结合。通过 Join 的交换和结合，可以找到所有逻辑等价的 GroupExpression。Join 的交换通过 JoinCommutativityRule 完成，逻辑比较简单，就是将孩子的左右孩子节点互换。需要注意的是，并不是只有 Inner Join 和 Cross Join 才可以进行互换，Outer Join 和 SemiJoin 同样可以。JoinCommutativityRule 中通过一个 Map 记录了 Join Type 发生交换时的改变，代码如下：

private static final Map<JoinOperator, JoinOperator> Join_COMMUTATIVITY_MAP =
        ImmutableMap.<JoinOperator, JoinOperator>builder()
                .put(JoinOperator.LEFT_ANTI_Join, JoinOperator.RIGHT_ANTI_Join)
                .put(JoinOperator.RIGHT_ANTI_Join, JoinOperator.LEFT_ANTI_Join)
                .put(JoinOperator.LEFT_SEMI_Join, JoinOperator.RIGHT_SEMI_Join)
                .put(JoinOperator.RIGHT_SEMI_Join, JoinOperator.LEFT_SEMI_Join)
                .put(JoinOperator.LEFT_OUTER_Join, JoinOperator.RIGHT_OUTER_Join)
                .put(JoinOperator.RIGHT_OUTER_Join, JoinOperator.LEFT_OUTER_Join)
                .put(JoinOperator.INNER_Join, JoinOperator.INNER_Join)
                .put(JoinOperator.CROSS_Join, JoinOperator.CROSS_Join)
                .put(JoinOperator.FULL_OUTER_Join, JoinOperator.FULL_OUTER_Join)
                .build();

例如 left outer Join 的孩子节点交换时，需要从 left outer 转换成 right outer。代码如下：

       left outer Join             right outer Join
       /           \      =>        /            \
      A             B              B              A

Join 的结合通过 JoinAssociativityRule 完成，主要逻辑可以用下面的图表示，Join 顺序的改变在Plan 中的改变就是树的形状变化。当然，在生成新的 OptExression 的过程中，也需要考虑 predicate 和 project 的重新分配。StarRocks 为 Join On 条件中包含表达式的结合转换做了支持，例如 SQL：

Select C.v4 from A Join B on A.v1 = B.v2 Join C on B.v2+1=C.v4 and B.v3 = C.V5

Join 上的 predicate 使用的列需要在孩子节点中包含，对于有 project 的进行表达式计算的，也需要考虑将其放在合适的 Join 上。例如下图中，须将 B.v3 = C.v5 放在新生成的 Join 节点上，如果 Table B 和 Table C 之间没有等值的谓词连接条件，StarRocks 会禁止转换，避免生成 CrossJoin 节点。Project 节点也需要在新生成的 Join 节点上重新计算，保证向上输出上层 Join 节点所需的 Column。

MultiJoinNode

为了加速多表（StarRocks 中为多于 4 表）Join reorder 的处理，StarRocks 中使用了 MultiJoinNode 来表示多张表的 Join。可以化简为以下代码：

public class MultiJoinNode {
    // Atom: A child of the Multi Join. This could be a table or some
    // other operator like a group by or a full outer Join.
    private final LinkedHashSet<OptExpression> atoms;
    private final List<ScalarOperator> predicates;
    private Map<ColumnRefOperator, ScalarOperator> expressionMap;

    public MultiJoinNode(LinkedHashSet<OptExpression> atoms, List<ScalarOperator> predicates,
                         Map<ColumnRefOperator, ScalarOperator> expressionMap) {
        this.atoms = atoms;
        this.predicates = predicates;
        this.expressionMap = expressionMap;
    }
 }

将多个 InnerJoin/CrossJoin 节点转换成 MultiJoinNode，其中需要 reorder 的孩子节点都表示成atoms。如下图所示，table A、B、C、D 就是各个 atom，所有的谓词记录在 predicates 中，后续算法将基于 MultiJoinNode 对 atom 进行重新组合，以产生合适的顺序。

左深树

如下图所示，左侧为左深树，右侧为稠密树。在单机／单任务数据库上，只需考虑左深树就可完成 Join 重排。当无法获取表的列统计信息时，无法准确估算 Join 的中间结果集，因此 StarRocks 选择了只生成左深树。

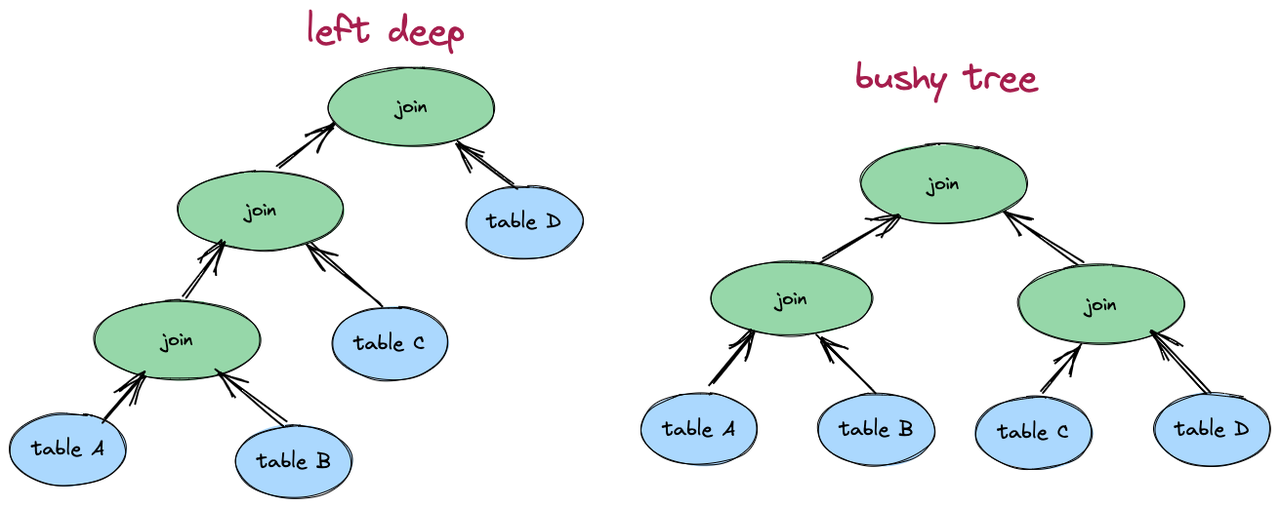
左深树的生成是由 JoinReorderLeftDeep 类完成的，逻辑比较简单。StarRocks 的 HashJoin 都是右表 build，左表 probe，期望生成的 Plan 中右表应该是小表，此方法中将需要 reorder 的 atom 按照 row count 从大到小进行排序，树最深的节点是代价最高的节点，这种 reorder 方法在没有列统计时也可以获得较为不错的表现。

动态规划

StarRocks 使用的是 DPsub 算法，通过将 atoms 划分成不同的 Partitions，递归计算子 Patition 的 bestPlan，并记录在 bestPlanMemo 中，从而实现规避重复计算。

例如，下图中的 [A,B] 就可以直接从 bestPlanMemo 中得到，而 [C,D] 则需要进一步递归分别得到 [C] 和 [D] 的 Best Plan，再计算 Join order [C,D] 的 Cost，并将 Cost 最小的 Join order 插入到 BestPlanMemo 中。最终包含所有 atom 的 Partition 即为 DP 算法选出的最佳 Plan。

这种 Bottom-Up 的 DP 算法可以有效处理稠密树空间枚举的问题，并能够利用动态规划来解决中间结果重复计算的问题，但由于需要枚举出所有子 Partition 的 Best Plan，atoms 过大时会导致优化时间太长，因此我们默认 10 个 Join 以内采用此方法。

贪心算法

如图，为贪心算法的实现：

在贪心算法的实现中，StarRocks 将 Join 分为了多个 Level。第一层就是每个 atom，从第一层中选择 Row Count 最小 atom 的和其他的 atom Join 生成 Join level 2。

其他 level 类比，Level K 从 Level K-1 中选择 Row Count 最小的，Join 其他的 atom，计算出 Level K 输出的 Row Count。当 K 等于 atom 个数时，算法结束，选出的即为最终“最优”的 Join Order。

这种方法的实现比较简单，贪心算法的原理也比较好理解，但不足之处在于只能用来构建左深树，且第一个 atom 的选择会对 Join Order 产生比较大的影响，容易陷入局部最优的问题。为了缓解这一问题，StarRocks 会启发式地生成 K 个 join 顺序，每个 Join 顺序选择的第一个 atom 都不一样，并将这些生成的 Plan 都 Copy In Memo，参与后续的 cost 计算，并从中选择 cost 最低的 plan。

总结

本文主要介绍了 StarRocks 中使用的 Join Reorder 算法和其基本原理。依据 Join 节点的个数不同，我们选用不同的 Join Reorder 算法，较少时用枚举法，10 个以内 Join 节点使用 DP 和贪心算法，超过 10 个时只使用贪心算法。通过对多种算法的使用，StarRocks 可以在 Join 较少时迅速找到最优解，在 Join 较多时也能在相对较短的时间内产生效果不错的 Plan。此外，为避免 Join Reorder 后的 Plan 只是单机最优，StarRocks 中还保留了多个算法产生 Join Order，以尽可能在 Memo 中找到分布式的最优解。

本期 StarRocks 源码解析到这就结束了，好学的你肯定学会了一些新东西，又产生了一些新困惑，不妨留言评论或者加入我们的社区一起交流（StarRocks 小助手微信号）。下一篇 StarRocks 源码解析，我们将为你带来 StarRocks 统计信息和 Cost 估算。