概念

栈

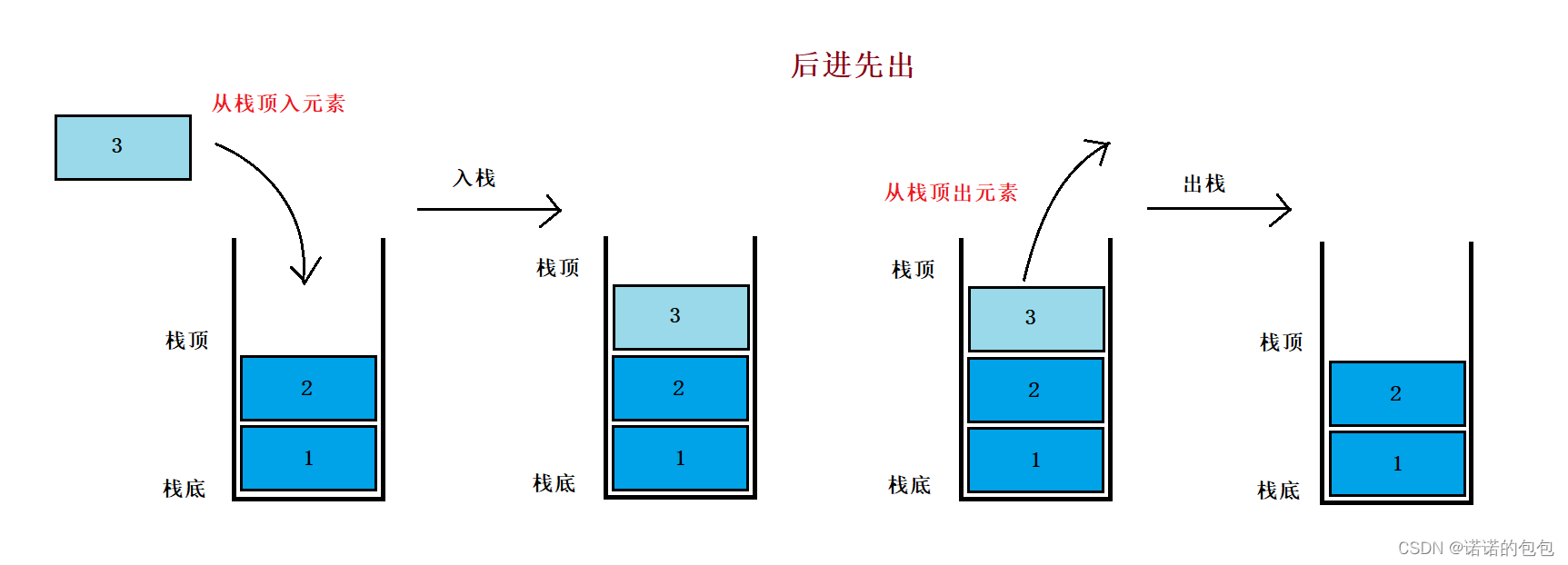
栈是一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。

压栈

栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。

出栈

栈的删除操作叫做出栈。出数据也在栈顶。

总结起来，即栈是一种特殊的线性表，数据的插入以及删除操作都在栈顶，遵循后进先出的原则，即后进来的元素在进行出栈时先于早进来的元素。

在这里插入图片描述

栈的实现

这里我们发现，实现栈的话，用单链表或者数组都可以，单链表的头插与头删就满足后进先出，而数组即我们前面写过的顺序表，数组的尾插与尾删也满足后进先出的原则。这两种实现方式的时间复杂度都为O（1），并无什么差别，这里我们就用顺序表（数组）来实现。

// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
	STDataType* _a;
	int _top;		// 栈顶
	int _capacity;  // 容量 
}Stack;

初始化栈

首先是初始化，这里我们先初始化为一个容量为4的栈,

// 初始化栈 
void StackInit(Stack* ps)
{
	assert(ps);
	ps->_a = (STDataType*)malloc(sizeof(STDataType)*4);
	ps->_top = 0;//栈顶元素的下一个
	ps->_capacity = 4;//栈的初始容量为4
}

这里需要注意的是，我们用_top来表示栈顶，_top== 0 和 top == -1是两个概念，等于0时表示的是栈顶的下一个，等于-1时才表示栈顶。如下图：
_top=-1
在这里插入图片描述
_top=0

注意两者区别即可。

入栈

接下来是入栈，这里我们由于是写的一个能动态增长的栈，所以我们再进行入元素之前，要先判断这个栈是否满了，如果满了的话，就要进行扩容。

// 入栈 
void StackPush(Stack* ps, STDataType data)
{
	assert(ps);
	//判断增容
	//_top==_capacity说明已经满了，要进行扩容
	if (ps->_top == ps->_capacity)
	{
		//容量调整为原来的二倍
		STDataType* tmp = realloc(ps->_a, 2 * ps->_capacity * sizeof(STDataType));
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		ps->_a = tmp;
		ps->_capacity *= 2;//记得更新_capacity
	}
	//接下来才是入栈，先入元素，_top再++。（假如_top初始化是-1的话，要先++，再入元素）
	ps->_a[ps->_top] = data;
	ps->_top++;
}

出栈

出栈的实现也很简单，就相当于数组尾删，直接_top- - 即可，不过要注意的是，假如栈是个空栈，就不能进行出栈操作了。这里我们用assert进行判断

// 出栈 
void StackPop(Stack* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));//判断是否为空
	ps->_top--;
}

获取栈顶元素

这里需要注意的是，由于我们一开始初始化的_top=0，它表示的是栈顶的下一个元素，原因上面也已经解释过了，所以我们获取栈顶元素时的下标实际为_top-1，不过注意空栈是不能获取栈顶元素的。

// 获取栈顶元素 
STDataType StackTop(Stack* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	return ps->_a[ps->_top - 1];
}

获取栈中有效元素个数

我们的_top其实就表示了我们的元素个数，因为我们是从0开始的，进一个元素之前就++了，假如是从-1开始的话，有效元素个数应为_top+1个。

// 获取栈中有效元素个数 
int StackSize(Stack* ps)
{
	assert(ps);
	return ps->_top;
}

判断栈是否为空

空栈就是_top等于0的情况下。

// 检测栈是否为空，如果为空返回true,否则false
bool StackEmpty(Stack* ps)
{
	assert(ps);
	return ps->_top == 0;
}

栈的销毁

释放malloc开辟的空间后，将所有元素置空置0

// 销毁栈 
void StackDestroy(Stack* ps)
{
	assert(ps);
	free(ps->_a);
	ps->_capacity = ps->_top = 0;
	ps->_a = NULL;
}

栈的应用

有人可能会问，这个东西能干嘛啊，其实它的作用也很大的，就比如后面要学的一些知识，比如二叉树的层序遍历、快排的非递归实现等等，都会用得到，这里我们拿一道力扣上的题来举个应用例子。
题目如下：

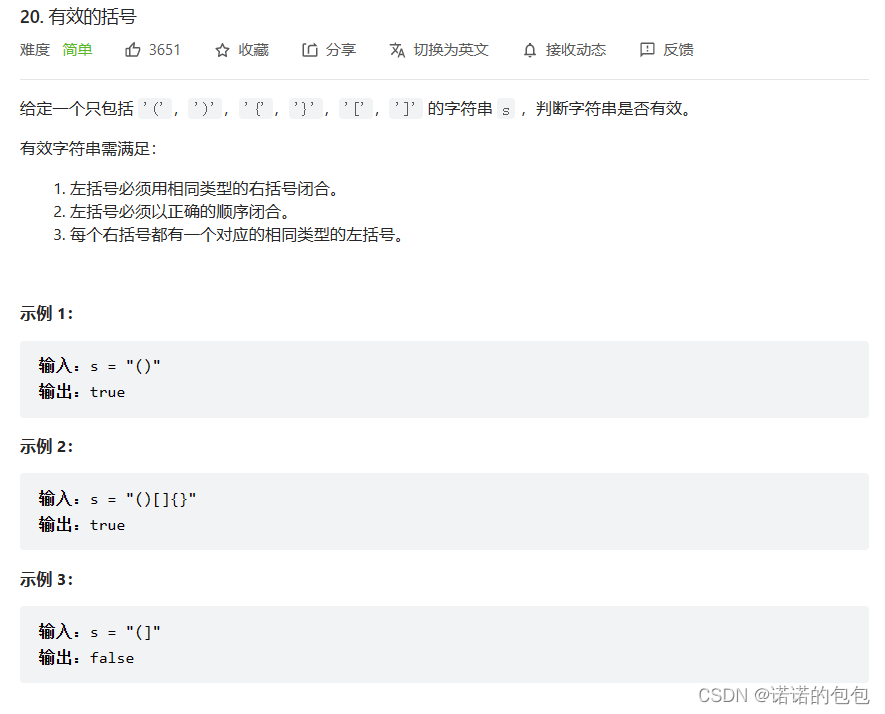
在这里插入图片描述
对于该题，以我们的水平，假如不知道栈的话，做这个可能有点小麻烦，可能有人说用双指针遍历等等，其实都很难解决，但是用栈的特点，就很好做了。

我们直接左括号入栈，当遇到右括号时出栈进行匹配，这里就用到了后进先出的特点完美解决问题。如下：

在这里插入图片描述
代码实现：（由于这里我们是用C语言写的，不像C++等语言可以直接调用库来使用，所以该题我们要自己创造出一个栈，就用我们上面写的，同时由于是字符串类型，所以记得将typedef int 改为char类型…）

这里由于为了不再重复的占用字数，我只将实现的代码写在下面，上面栈的实现直接拷贝到该函数上面即可。

void StackDestroy(Stack* ps)
{
	assert(ps);
	free(ps->_a);
	ps->_capacity = ps->_top = 0;
	ps->_a = NULL;
}
bool isValid(char * s){
    Stack st;
    //初始化栈
    StackInit(&st);
    while(*s)
    {
        //左括号入栈
        if(*s == '[' || *s=='('|| *s== '{')
        {
            StackPush(&st,*s);
            s++;
        }
        else
        {
            //假如没有左括号，空栈
            if(StackEmpty(&st))
            {
                return false;
            }
            //top存放栈顶元素
            char top=StackTop(&st);
            StackPop(&st);//出栈
            //进行对比
            if((*s==']'&& top !='[')
            ||(*s==')'&& top !='(')
            ||(*s=='}'&& top !='{'))
            {
                StackDestroy(&st);
                return false;
            }
            else
            {
                s++;
            }
        }
    }
    //栈不为空
    bool ret=StackEmpty(&st);
    StackDestroy(&st);
    return ret;
}