机器学习 第三课 k 近邻
- 概述
- 机器学习简介
- K 近邻算法
- K 近邻中的距离
- 欧氏距离
- 曼哈顿距离
- 余弦相似度
- 选择合适的 K 值
- 奇数 vs 偶数
- 通过交叉验证选择 k 值
- 实战
- 分类问题
- 回归问题
- K 近邻算法的优缺点
- 优点
- 缺点
- 手把手实现 k 近邻
- 手搓算法
- 实战分类
概述
机器学习 (Machine Learning) 已经成为现代科技领域不可或缺的一个分支, 涉及到各种应用, 从自动驾驶, 到人脸识别, 到推荐系统为我们推荐歌曲. 在众多的机器学习算法中, K 近邻算法是最为简单的一个. K 近邻算法有着简单和直观的原理.

机器学习简介
当我们提到机器学习 (Machine Learning) 时, 我们实际上是指让机器从数据中学习并做出决策或预测的过程. 这与传统的编程方法形成对比, 传统方法中, 我们需要明确告诉机器如何执行任务. 但在机器学习中, 机器会根据提供的数据 “学习” 如何执行任务.
例如, 如果我们希望机器识别出一张图片上的猫, 传统的方法可能需要你定义猫的特征, 如耳朵的形状, 眼睛的大小等. 但在机器学习中, 你会提供成千上万的猫的图片 (和非猫的图片), 让机器自己找出猫的特征.
K 近邻算法
K 近邻 (k-Nearest Neighbor) 是机器学习中一种基础算法. K 近邻的核心思想是 “物以类聚”. 通过查找一个未知数据在训练集中最相近的 “k” 个点, 并更加近似数据的标签来预测未标记数据的标签.
举个栗子:
如果小白我到了一个新的城市, 想找个地方吃饭, 我会询问几个当地人, 如果多个人推荐了同一个餐厅, 我们大概率会去选择他们推荐的餐馆. 在这个例子中, 当地人 (城市居民) 就是我们的 “邻居”, 这些邻居的推荐是基于他们的经验. K 近邻算法就是这样工作的, 通过考虑周围的 “邻居” 并根据他们的 “推荐” 做出决策.
K 近邻中的距离
K 近邻算法的关键是如何计算数据之间的距离 (Distance). K 近邻的算法依赖于找出一个点的最近邻居, “最近” 就是通过距离远近来定义的.
欧氏距离
欧氏距离 (Euclidean Distance) 是最常见的距离计算方法. 简单的来说欧氏距离就是两点之间的直线距离, 我们可以通过小学学过的勾股定理来计算. 在多维空间中, 欧氏距离为每一个维度的差值的平方和平方根.
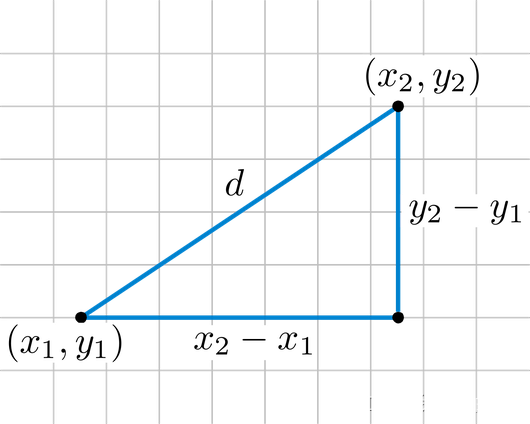
计算公式:
e
u
c
l
i
d
e
a
n
d
i
s
t
a
n
c
e
=
(
(
x
2
−
x
1
)
2
+
(
y
2
−
y
1
)
2
)
euclidean \; distance = \sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)
euclideandistance=((x2−x1)2+(y2−y1)2)
我们数据中的每个特征 (Feature) 可视为一个维度, 例如乳腺癌分类数据集中的 radius_mean, texture_mean. 如果我们有多个特征, 只需扩展上述公式.
例如:
- 2 个特征: e u c l i d e a n d i s t a n c e = ( ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 ) euclidean \; distance = \sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2) euclideandistance=((x2−x1)2+(y2−y1)2)
- 3 个特征: e u c l i d e a n d i s t a n c e = ( ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + ( z 2 − z 1 ) 2 ) euclidean \; distance = \sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2) euclideandistance=((x2−x1)2+(y2−y1)2+(z2−z1)2)
- 4 个特征: e u c l i d e a n d i s t a n c e = ( ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + ( z 2 − z 1 ) 2 + ( a 2 − a 1 ) 2 ) euclidean \; distance = \sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2 + (a_2 - a_1)^2) euclideandistance=((x2−x1)2+(y2−y1)2+(z2−z1)2+(a2−a1)2)
例子:
from sklearn.neighbors import KNeighborsClassifier
# 使用欧几里得距离
knn_euclidean = KNeighborsClassifier(n_neighbors=5, metric='euclidean')
knn_euclidean.fit(X, y)
曼哈顿距离
曼哈顿距离 (Manhattan Distance) 是通过计算在一个格子形状路径上从第一个点到另一个点的总距离, 及沿轴绝对差值的总和.
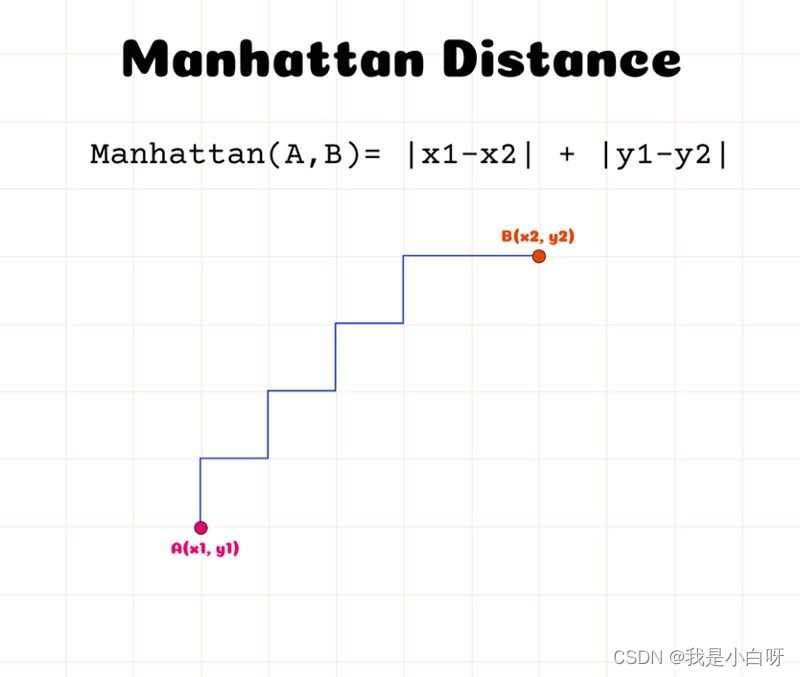
计算公式:
m
a
n
h
a
t
t
a
n
d
i
s
t
a
n
c
e
=
∣
x
1
−
x
2
∣
+
∣
y
1
−
y
2
∣
manhattan \; distance = |x_1 - x_2| + |y_1 - y_2|
manhattandistance=∣x1−x2∣+∣y1−y2∣
同理, 如果我们有多个特征, 只需扩展上述公式:
- 2 个特征: m a n h a t t a n d i s t a n c e = ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ manhattan \; distance = |x_1 - x_2| + |y_1 - y_2| manhattandistance=∣x1−x2∣+∣y1−y2∣$
- 3 个特征: m a n h a t t a n d i s t a n c e = ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ + ∣ z 1 − z 2 ∣ manhattan \; distance = |x_1 - x_2| + |y_1 - y_2| + |z_1 - z_2| manhattandistance=∣x1−x2∣+∣y1−y2∣+∣z1−z2∣
- 4 个特征: m a n h a t t a n d i s t a n c e = ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ + ∣ z 1 − z 2 ∣ + ∣ a 1 − a 2 ∣ manhattan \; distance = |x_1 - x_2| + |y_1 - y_2| + |z_1 - z_2| + |a_1 - a_2| manhattandistance=∣x1−x2∣+∣y1−y2∣+∣z1−z2∣+∣a1−a2∣
例子:
from sklearn.neighbors import KNeighborsClassifier
# 使用曼哈顿距离
knn_manhattan = KNeighborsClassifier(n_neighbors=5, metric='manhattan')
knn_manhattan.fit(X, y)
余弦相似度
余弦相似度 (Cosine Similarity) 是通过计算两个向量的夹角来判断相似度. 当我们遇到需要数据之间的方向而不是绝对距离的时候会用到余弦相似度. 举个例子, 在文本分析中判断文本的相似度 (距离).
选择合适的 K 值
K 值的选择对 K 近邻算法来说非常重要. K 值决定了算法需要考虑的 “邻居” 的数量. 如果 k=1, 意味着只用一个 “邻居” 对结果进行预测, 容易造成过度拟合的问题; 如果 k 的取值过大, 意味着不那么相似的 “邻居” 也会影响到模型的判断.
举个栗子, 当我们到了一个陌生的城市, 想找一个地方吃饭:
- k=1 (考虑一个最近的邻居): 我们只问了一个路过的人他最喜欢的餐馆. 有概率这个人可能喜欢偏僻, “味道独特” 的小店, 然而大概率我们并不喜欢. 由于我们参考了一个人的意见 (k=1), 所以我们可能错过了该城市真正受欢迎的餐馆. 同理, 当我们选择的 k 值过小的时候, 模型就会收到各别异常意见的影响, 过度拟合.
- k=∞ (考虑所有邻居): 我们问变了每个路过的人, 得到了上百条建议, 然后选择了大多数人都提到的餐馆 (沙县小吃, 兰州牛肉面). 这可能是一个非常普通和大众的连锁店, 但不会是一个你想要的地方特色餐馆. 同理, 当我们选择的 k 值过大的时候, 和你不那么相近的 “邻居” 也会影响到模型, 导致模型过度简化 (欠拟合).
奇数 vs 偶数
选择奇数作为 k 值可以避在二分类中平局的情况. 例如一个二分类问题, k=2 时, 俩邻居意见不同.
通过交叉验证选择 k 值
from sklearn.model_selection import cross_val_score
from sklearn.neighbors import KNeighborsClassifier
# 假设我们有数据 X, y
best_score = 0
best_k = 1
for k in range(1, 31):
knn = KNeighborsClassifier(n_neighbors=k)
scores = cross_val_score(knn, X, y, cv=10)
mean_score = scores.mean()
if mean_score > best_score:
best_score = mean_score
best_k = k
print(f"Best k value: {best_k}")
实战
分类问题
我们拿鸢尾花数据集来带大家实践一下 KNN 算法. 鸢尾花数据集包三种鸢尾花, 各50组数据构成的数据集. 每个样本包含 4 个特征, 分别为萼片 (sepals) 的长和宽, 花瓣 (petals) 的长和宽. 通过 K 近邻算法, 我们可以来预测花的种类.
例子:
"""
@Module Name: knn分类.py
@Author: CSDN@我是小白呀
@Date: October 16, 2023
Description:
使用 K近邻算法对鸢尾花进行分类
"""
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score, recall_score, f1_score
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 调试输出数据基本信息
print("输出特征:", X[:5])
print("输出标签:", y[:5])
# 分割数据集
X_train, X_vaild, y_train, y_vaild = train_test_split(X, y, test_size=0.2)
# 实例化模型
knn = KNeighborsClassifier(n_neighbors=3)
# 训练模型
knn.fit(X_train, y_train)
# 预测
y_pred = knn.predict(X_vaild)
# 评估指标
print("精度:", accuracy_score(y_vaild, y_pred))
print("召回率:", recall_score(y_vaild, y_pred, average='macro')) # 多分类问题使用宏平均
print("F1分数:", f1_score(y_vaild, y_pred, average='macro')) # 多分类问题使用宏平均
输出结果:
输出特征: [[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]]
输出标签: [0 0 0 0 0]
精度: 0.9
召回率: 0.8777777777777779
F1分数: 0.8656126482213438
我们进一步优化一下以上代码:
"""
@Module Name: knn分类.py
@Author: CSDN@我是小白呀
@Date: October 16, 2023
Description:
使用 K近邻算法对鸢尾花进行分类
"""
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import classification_report
from matplotlib import pyplot as plt
plt.style.use("fivethirtyeight")
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 调试输出数据基本信息
print("输出特征:", X[:5])
print("输出标签:", y[:5])
# 分割数据集
X_train, X_vaild, y_train, y_vaild = train_test_split(X, y, test_size=0.2)
# 通过交叉验证选择k值
k_value_score = []
for k in range(1, 31):
knn = KNeighborsClassifier(n_neighbors=k)
scores = cross_val_score(knn, X, y, cv=10)
mean_score = scores.mean()
k_value_score.append(mean_score)
# 绘图
plt.figure(figsize=(12, 8))
plt.plot([i for i in range(1, 31)], k_value_score)
plt.xlabel('Value of K for KNN')
plt.ylabel('Score')
plt.show()
# 实例化模型
knn = KNeighborsClassifier(n_neighbors=12)
# 训练模型
knn.fit(X_train, y_train)
# 预测
y_pred = knn.predict(X_vaild)
# 评估指标
print(classification_report(y_vaild, y_pred))
输出结果:
输出特征: [[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]]
输出标签: [0 0 0 0 0]
precision recall f1-score support
0 1.00 1.00 1.00 10
1 0.90 1.00 0.95 9
2 1.00 0.91 0.95 11
accuracy 0.97 30
macro avg 0.97 0.97 0.97 30
weighted avg 0.97 0.97 0.97 30
回归问题
波士顿房价数据集是一个经典的回归数据集, 其中包含了波士顿各个城区的房屋中位数价格与其他相关特征, 如犯罪率, 教育水平等. 使用K近邻回归, 我们可以预测新的城区的房价.
代码:
"""
@Module Name: knn回归.py
@Author: CSDN@我是小白呀
@Date: October 16, 2023
Description:
使用 K近邻算法预测波士顿房价
"""
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error
# 加载数据集
boston = load_boston()
X = boston.data
y = boston.target
# 调试输出数据基本信息
print("输出特征:", X[:5])
print("输出标签:", y[:5])
# 分割数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# K 近邻回归
knn_reg = KNeighborsRegressor(n_neighbors=5)
knn_reg.fit(X_train, y_train)
# 预测
y_pred = knn_reg.predict(X_test)
print("平方差:", mean_squared_error(y_test, y_pred))
输出结果:
输出特征: [[6.3200e-03 1.8000e+01 2.3100e+00 0.0000e+00 5.3800e-01 6.5750e+00
6.5200e+01 4.0900e+00 1.0000e+00 2.9600e+02 1.5300e+01 3.9690e+02
4.9800e+00]
[2.7310e-02 0.0000e+00 7.0700e+00 0.0000e+00 4.6900e-01 6.4210e+00
7.8900e+01 4.9671e+00 2.0000e+00 2.4200e+02 1.7800e+01 3.9690e+02
9.1400e+00]
[2.7290e-02 0.0000e+00 7.0700e+00 0.0000e+00 4.6900e-01 7.1850e+00
6.1100e+01 4.9671e+00 2.0000e+00 2.4200e+02 1.7800e+01 3.9283e+02
4.0300e+00]
[3.2370e-02 0.0000e+00 2.1800e+00 0.0000e+00 4.5800e-01 6.9980e+00
4.5800e+01 6.0622e+00 3.0000e+00 2.2200e+02 1.8700e+01 3.9463e+02
2.9400e+00]
[6.9050e-02 0.0000e+00 2.1800e+00 0.0000e+00 4.5800e-01 7.1470e+00
5.4200e+01 6.0622e+00 3.0000e+00 2.2200e+02 1.8700e+01 3.9690e+02
5.3300e+00]]
输出标签: [24. 21.6 34.7 33.4 36.2]
平方差: 47.335607843137254
K 近邻算法的优缺点
优点
- 简单易懂: KNN 是基于实力的学习, 算法简单直观, 易于理解. 对于简单的分类和回归的任务, 仅需要几行代码
- 无需训练步骤: KNN 是一种懒惰学习器 (Lazy Leaner) 即 KNN 实际上不会在数据上训练一个模型, 而是在预测时使用训练数据
- 自热的处理多分类问题: 无需额外的修改即可处理多个类别
- 可用于分类和回归: KNN 既可以用于分类任务, 也可以用于回归任务, 使用具有多功能性
缺点
- 计算密集型: 由于算法需要为每个新的数据搜索 k 个最近值, 因此在大数据集计算成本直线上升
- 对不平衡数据敏感: 在数据集中, 如果某个类的数据量大于另一个类, 那么数据很可能会分类为该大类
手把手实现 k 近邻
为了帮助大家更好的理解, 小白我带领大家手把手实现一下 knn 算法.
手搓算法
手搓 KNN:
"""
@Module Name: 手把手实现knn.py
@Author: CSDN@我是小白呀
@Date: October 16, 2023
Description:
手把手实现knn算法
"""
class KNN:
def __init__(self, k=3):
"""
初始化参数
:param k: k值, 默认为 3
"""
self.k = k
self.X_train = None
self.y_train = None
def fit(self, X_train, y_train):
"""
为训练集 / 测试集成员赋值
:param X_train: 训练集
:param y_train: 测试集
:return:
"""
self.X_train = X_train
self.y_train = y_train
def predict(self, X_test):
"""
预测
:param X_test: 训练特征集
:return: 预测值
"""
y_pred = [self._predict(x) for x in X_test]
return y_pred
def _predict(self, x):
"""
预测
:param x: 需要预测的数据
:return: 预测标签
"""
# 计算距离
distances = [self._euclidean_distance(x, x_train) for x_train in self.X_train]
# 得到 k 个最近邻的索引
k_indices = sorted(range(len(distances)), key=lambda i: distances[i])[:self.k]
# k个最近邻的标签
k_nearest_labels = [self.y_train[i] for i in k_indices]
# 投票
most_common = self._vote(k_nearest_labels)
# 返回标签
return most_common
def _euclidean_distance(self, x1, x2):
"""
计算欧式距离
:param x1: 数据1
:param x2: 数据2
:return: 距离
"""
return sum((xi - xj) ** 2 for xi, xj in zip(x1, x2)) ** 0.5
def _vote(self, labels):
# 使用字典统计每个类别的票数
votes = {}
for label in labels:
if label in votes:
votes[label] += 1
else:
votes[label] = 1
# 根据票数排序并返回得票数最多的类别
return sorted(votes.items(), key=lambda x: x[1], reverse=True)[0][0]
实战分类
用手搓 KNN 进行鸢尾花分类:
"""
@Module Name: 手把手实现knn.py
@Author: CSDN@我是小白呀
@Date: October 16, 2023
Description:
手把手实现knn算法
"""
class KNN:
def __init__(self, k=3):
"""
初始化参数
:param k: k值, 默认为 3
"""
self.k = k
self.X_train = None
self.y_train = None
def fit(self, X_train, y_train):
"""
为训练集 / 测试集成员赋值
:param X_train: 训练集
:param y_train: 测试集
:return:
"""
self.X_train = X_train
self.y_train = y_train
def predict(self, X_test):
"""
预测
:param X_test: 训练特征集
:return: 预测值
"""
y_pred = [self._predict(x) for x in X_test]
return y_pred
def _predict(self, x):
"""
预测
:param x: 需要预测的数据
:return: 预测标签
"""
# 计算距离
distances = [self._euclidean_distance(x, x_train) for x_train in self.X_train]
# 得到 k 个最近邻的索引
k_indices = sorted(range(len(distances)), key=lambda i: distances[i])[:self.k]
# k个最近邻的标签
k_nearest_labels = [self.y_train[i] for i in k_indices]
# 投票
most_common = self._vote(k_nearest_labels)
# 返回标签
return most_common
def _euclidean_distance(self, x1, x2):
"""
计算欧式距离
:param x1: 数据1
:param x2: 数据2
:return: 距离
"""
return sum((xi - xj) ** 2 for xi, xj in zip(x1, x2)) ** 0.5
def _vote(self, labels):
# 使用字典统计每个类别的票数
votes = {}
for label in labels:
if label in votes:
votes[label] += 1
else:
votes[label] = 1
# 根据票数排序并返回得票数最多的类别
return sorted(votes.items(), key=lambda x: x[1], reverse=True)[0][0]
if __name__ == '__main__':
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 调试输出数据基本信息
print("输出特征:", X[:5])
print("输出标签:", y[:5])
# 分割数据集
X_train, X_vaild, y_train, y_vaild = train_test_split(X, y, test_size=0.2)
# 实例化模型
knn = KNN(12)
# 训练模型
knn.fit(X_train, y_train)
# 预测
y_pred = knn.predict(X_vaild)
# 评估指标
print(classification_report(y_vaild, y_pred))
输出结果:
输出特征: [[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]]
输出标签: [0 0 0 0 0]
precision recall f1-score support
0 1.00 1.00 1.00 8
1 0.83 1.00 0.91 10
2 1.00 0.83 0.91 12
accuracy 0.93 30
macro avg 0.94 0.94 0.94 30
weighted avg 0.94 0.93 0.93 30








![2023年全球及中国多肽CDMO市场发展概述分析:CDMO头部企业将拓展至多肽领域[图]](https://img-blog.csdnimg.cn/img_convert/95111679129fb081eefe42f531fbd70c.png)