1、二叉树基本操作

二叉树的定义就不在这里多说了，下面这个图就是一个简单的二叉树：

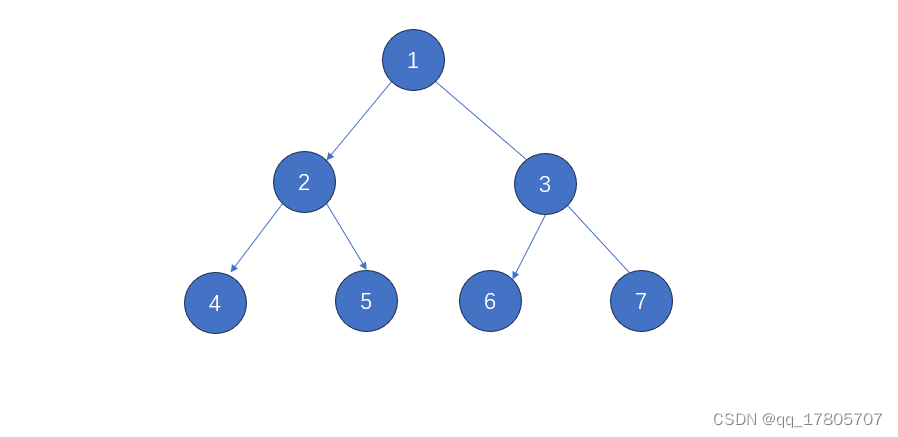二叉树的三种遍历方式：

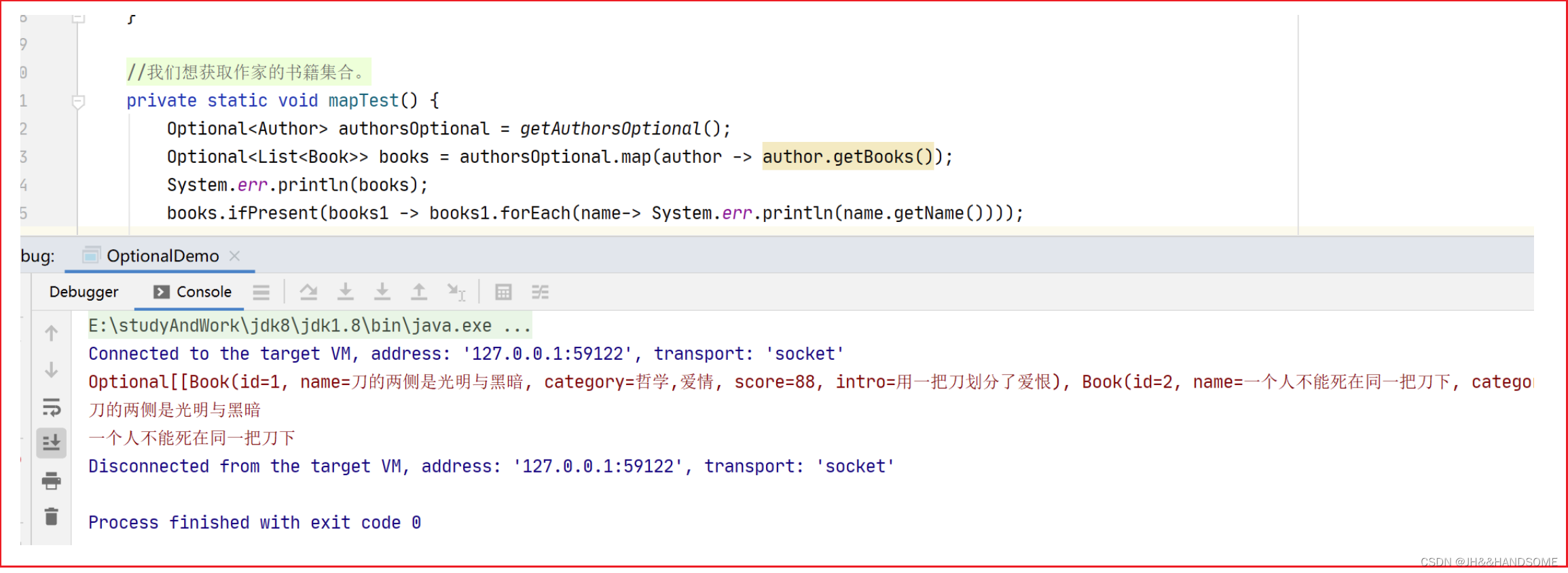
前序遍历：头左右，也就是先头后左再右：1245367

    public static void prePrint(BinaryTreeNode root) {
        if (root != null) {
            System.err.print(root.val);
            prePrint(root.left);
            prePrint(root.right);
        }
    }

中序遍历：左头右，也就是先左后头再右：4251637

    public static void midPrint(BinaryTreeNode root) {
        if (root != null) {
            midPrint(root.left);
            System.err.print(root.val);
            midPrint(root.right);
        }
    }

后序遍历：左头右，也就是先左后右再头：4526731

    public static void posPrint(BinaryTreeNode root) {
        if (root != null) {
            posPrint(root.left);
            posPrint(root.right);
            System.err.print(root.val);
        }
    }

测试代码：

class BinaryTreeNode {
    int val;
    BinaryTreeNode left;
    BinaryTreeNode right;


    public BinaryTreeNode(int val) {
        this.val = val;
    }

    public BinaryTreeNode(int val, BinaryTreeNode left, BinaryTreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

    public static void main(String[] args) {
        BinaryTreeNode one = new BinaryTreeNode(1,
                new BinaryTreeNode(2, new BinaryTreeNode(4, null, null), new BinaryTreeNode(5, null, null)),
                new BinaryTreeNode(3, new BinaryTreeNode(6, null, null), new BinaryTreeNode(7, null, null)));
        prePrint(one);
        System.err.println();
        midPrint(one);
        System.err.println();
        posPrint(one);
    }

那么我们可以看出来，不论是哪种遍历方式，其在处理左右子节点的时候，逻辑都是一样的，都是要递归处理，不同的只是头结点的输出时机，那么可以优化成下面的代码：

    public static void print(BinaryTreeNode root, int type) {
        switch (type) {
            case 1:
                if (root != null) {
                    System.err.print(root.val);
                    print(root.left, 1);
                    print(root.right, 1);
                }
                break;
            case 2:
                if (root != null) {
                    print(root.left, 2);
                    System.err.print(root.val);
                    print(root.right, 2);
                }
                break;
            case 3:
                if (root != null) {
                    print(root.left, 3);
                    print(root.right, 3);
                    System.err.print(root.val);
                }
                break;
        }
    }

2、两棵树是否结构一样

如下面的图中，只有左上角和右上角两棵树的结构是一样的，才算符合条件：

Java实现判断两棵树是否一样：

    public static boolean isSameTree(BinaryTreeNode node1, BinaryTreeNode node2) {
        if (node1 == null ^ node2 == null) {
            return false;
        }
        if (node1 == null && node2 == null) {
            return true;
        }
        return node1.val == node2.val && isSameTree(node1.left, node2.left) && isSameTree(node1.right, node2.right);
    }

    @Test
    public void testSame() {
        BinaryTreeNode one = new BinaryTreeNode(1,
                new BinaryTreeNode(2, new BinaryTreeNode(4, null, null), new BinaryTreeNode(5, null, null)),
                new BinaryTreeNode(3, new BinaryTreeNode(6, null, null), new BinaryTreeNode(7, null, null)));
        BinaryTreeNode two = new BinaryTreeNode(1,
                new BinaryTreeNode(2, new BinaryTreeNode(4, null, null), new BinaryTreeNode(5, null, null)),
                new BinaryTreeNode(3, new BinaryTreeNode(6, null, null), new BinaryTreeNode(7, null, null)));
        System.err.println(isSameTree(one, two));
    }

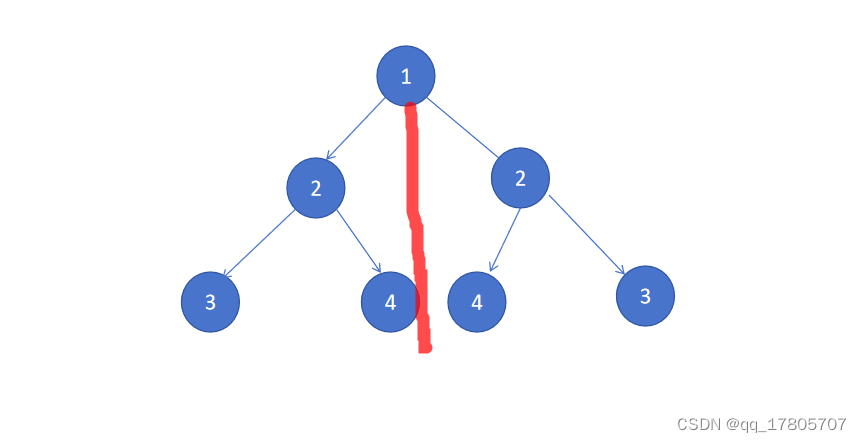
3、镜面树

镜面树有两种情况：

1. 两棵树互为镜面：按照红线对折，可以重叠 
2. 单棵树两边互为镜面：代码实现：

       public static boolean isMirror(BinaryTreeNode node1, BinaryTreeNode node2) {
           if (node1 == null ^ node2 == null) {
               return false;
           }
           if (node1 == null && node2 == null) {
               return true;
           }
           return node1.val == node2.val && isMirror(node1.left, node2.right) && isMirror(node1.right, node2.left);
       }
   
       @Test
       public void testMirror() {
           BinaryTreeNode one = new BinaryTreeNode(1,
                   new BinaryTreeNode(2, new BinaryTreeNode(4, null, null), new BinaryTreeNode(5, null, null)),
                   new BinaryTreeNode(2, new BinaryTreeNode(5, null, null), new BinaryTreeNode(4, null, null)));
           BinaryTreeNode two = new BinaryTreeNode(1,
                   new BinaryTreeNode(2, new BinaryTreeNode(4, null, null), new BinaryTreeNode(5, null, null)),
                   new BinaryTreeNode(2, new BinaryTreeNode(5, null, null), new BinaryTreeNode(4, null, null)));
           System.err.println(isMirror(one, two));
       }

 4、树的最大深度

二叉树的最大深度其实就是左子树和右子树的最大深度加一，代码实现如下：

    public static int maxDepth(BinaryTreeNode root) {
        if (root == null) {
            return 0;
        }
        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }

    @Test
    public void testMaxDepth() {
        BinaryTreeNode two = new BinaryTreeNode(1,
                new BinaryTreeNode(2, new BinaryTreeNode(4, null, null), new BinaryTreeNode(5, null, null)),
                new BinaryTreeNode(2, new BinaryTreeNode(5, null, null), new BinaryTreeNode(4, null, null)));
        System.err.println(maxDepth(two));
    }