1.题目链接：有效三角形的个数

2.题目描述：

给定一个包含非负整数的数组 nums ，返回其中可以组成三角形三条边的三元组个数。

示例 1:

输入: nums = [2,2,3,4]
输出: 3
解释:有效的组合是: 
2,3,4 (使用第一个 2)
2,3,4 (使用第二个 2)
2,2,3

示例 2:

输入: nums = [4,2,3,4]
输出: 4

提示:

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 1000

3.算法代码：

解法1：暴力枚举（会超时）

三层for循环枚举出所有的三元组，并且判断是否能构成三⻆形，然后count累加

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        int i,j,k;
        int count=0;
        for(i=0;i<nums.size();i++)
        {
            for(j=i+1;j<nums.size();j++)
            {
                for(k=j+1;k<nums.size();k++)
                {
                    if(nums[i]+nums[j]>nums[k])
                    {
                        count++;
                    }
                }
            }
        }
        return count;
    }
};

解法2：排序+双指针

1. 先将数组排序

2. 固定最大的数

3. 在最大数的左区间内，使用双指针算法快速统计出符合要求的三元组的个数

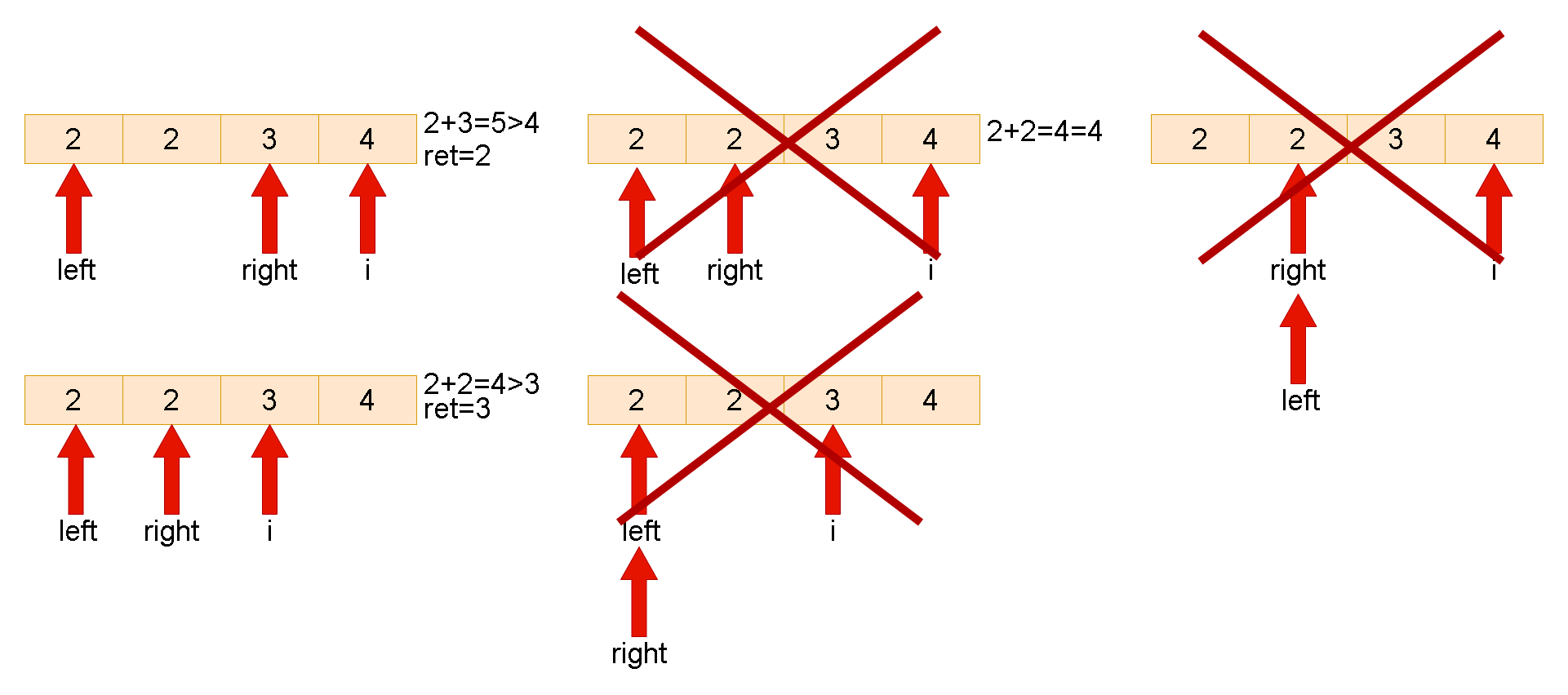
   • 如果 nums[left] + nums[right] > nums[i] ：

     • 说明[left, right - 1]区间上的所有元素均可以与 nums[right] 构成⽐nums[i]⼤的⼆元组
     • 满⾜条件的有right - left 种，此时 right 位置的元素的所有情况相当于全部考虑完毕， right-- ，进⼊下⼀轮判断

   • 如果 nums[left] + nums[right] <= nums[i] ：

     • 说明 left 位置的元素是不可能与 [left + 1, right] 位置上的元素构成满⾜条件的⼆元组，
     • left 位置的元素可以舍去 left++ 进⼊下轮循环
       

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        //排序
        sort(nums.begin(),nums.end());
        //双指针
        int ret=0,n=nums.size();
        for(int i=n-1;i>=2;i--)
        {
            int left=0,right=i-1;
            while(left<right)
            {
                if(nums[left]+nums[right]>nums[i])
                {
                    ret+=right-left;
                    right--;
                }
                else
                {
                    left++;
                }
            }
        }
          return ret;
    }
  
};