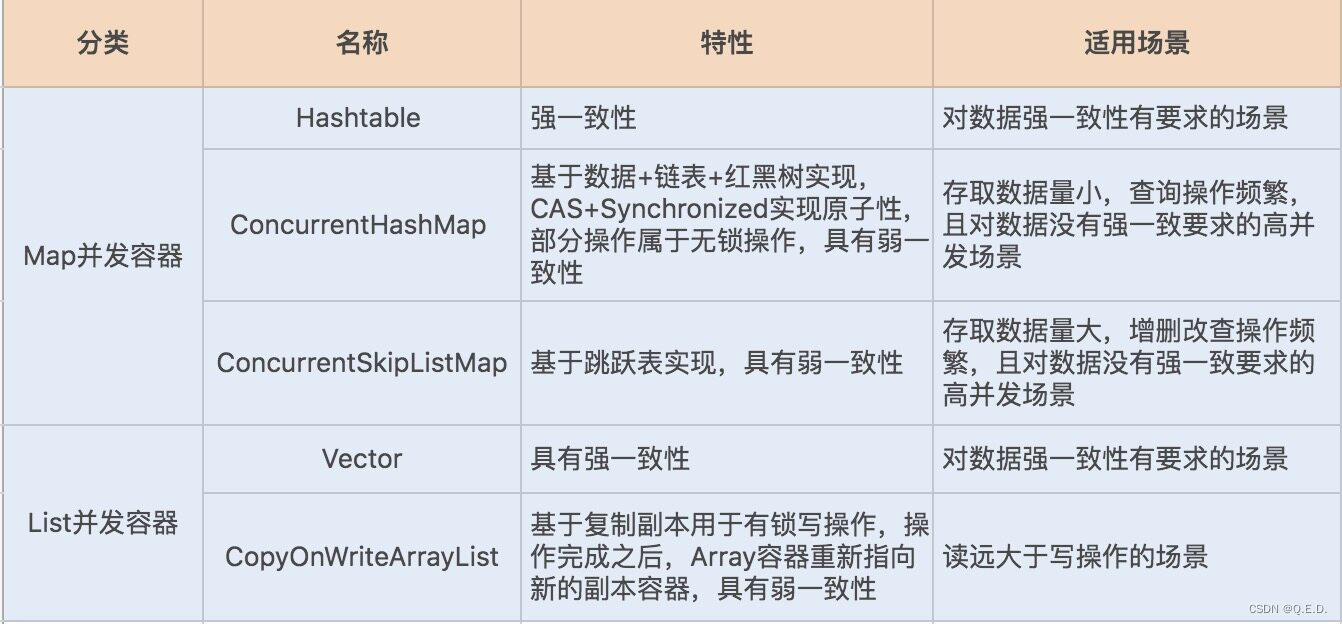
1 文本格式
using System;
using System.Collections.Generic;
namespace Legalsoft.Truffer
{
public class Gaumixmod
{
private int nn { get; set; }
private int kk { get; set; }
private int mm { get; set; }
private double[,] data { get; set; }
private double[,] means { get; set; }
private double[,] resp { get; set; }
private double[] frac { get; set; }
private double[] lndets { get; set; }
private double[,,] sig { get; set; }
private double loglike { get; set; }
public Gaumixmod(double[,] ddata, double[,] mmeans)
{
int mmstat = ddata.GetLength(1);
this.nn = ddata.GetLength(0);
this.kk = mmeans.GetLength(0);
this.mm = mmstat;
this.data = Globals.CopyFrom(ddata);
this.means = Globals.CopyFrom(mmeans);
this.resp = new double[nn, kk];
this.frac = new double[kk];
this.lndets = new double[kk];
this.sig = new double[kk, mmstat, mmstat];
for (int k = 0; k < kk; k++)
{
frac[k] = 1.0 / kk;
for (int i = 0; i < mm; i++)
{
for (int j = 0; j < mm; j++)
{
sig[k, i, j] = 0.0;
}
sig[k, i, i] = 1.0e-10;
}
}
estep();
mstep();
}
public double estep()
{
double[] u = new double[mm];
double[] v = new double[mm];
double oldloglike = loglike;
for (int k = 0; k < kk; k++)
{
//Cholesky choltmp = new Cholesky(sig[k]);
Cholesky choltmp = new Cholesky(Globals.CopyFrom(k, sig));
lndets[k] = choltmp.logdet();
for (int n = 0; n < nn; n++)
{
for (int m = 0; m < mm; m++)
{
u[m] = data[n, m] - means[k, m];
}
choltmp.elsolve(u, v);
double sum = 0.0;
for (int m = 0; m < mm; m++)
{
sum += Globals.SQR(v[m]);
}
resp[n, k] = -0.5 * (sum + lndets[k]) + Math.Log(frac[k]);
}
}
loglike = 0;
for (int n = 0; n < nn; n++)
{
double max = -99.9e99;
for (int k = 0; k < kk; k++)
{
if (resp[n, k] > max)
{
max = resp[n, k];
}
}
double sum = 0.0;
for (int k = 0; k < kk; k++)
{
sum += Math.Exp(resp[n, k] - max);
}
double tmp = max + Math.Log(sum);
for (int k = 0; k < kk; k++)
{
resp[n, k] = Math.Exp(resp[n, k] - tmp);
}
loglike += tmp;
}
return loglike - oldloglike;
}
public void mstep()
{
for (int k = 0; k < kk; k++)
{
double wgt = 0.0;
for (int n = 0; n < nn; n++)
{
wgt += resp[n, k];
}
frac[k] = wgt / nn;
for (int m = 0; m < mm; m++)
{
double sum = 0.0;
for (int n = 0; n < nn; n++)
{
sum += resp[n, k] * data[n, m];
}
means[k, m] = sum / wgt;
for (int j = 0; j < mm; j++)
{
sum = 0.0;
for (int n = 0; n < nn; n++)
{
sum += resp[n, k] * (data[n, m] - means[k, m]) * (data[n, j] - means[k, j]);
}
sig[k, m, j] = sum / wgt;
}
}
}
}
}
}
2 代码格式
using System;
using System.Collections.Generic;
namespace Legalsoft.Truffer
{
public class Gaumixmod
{
private int nn { get; set; }
private int kk { get; set; }
private int mm { get; set; }
private double[,] data { get; set; }
private double[,] means { get; set; }
private double[,] resp { get; set; }
private double[] frac { get; set; }
private double[] lndets { get; set; }
private double[,,] sig { get; set; }
private double loglike { get; set; }
public Gaumixmod(double[,] ddata, double[,] mmeans)
{
int mmstat = ddata.GetLength(1);
this.nn = ddata.GetLength(0);
this.kk = mmeans.GetLength(0);
this.mm = mmstat;
this.data = Globals.CopyFrom(ddata);
this.means = Globals.CopyFrom(mmeans);
this.resp = new double[nn, kk];
this.frac = new double[kk];
this.lndets = new double[kk];
this.sig = new double[kk, mmstat, mmstat];
for (int k = 0; k < kk; k++)
{
frac[k] = 1.0 / kk;
for (int i = 0; i < mm; i++)
{
for (int j = 0; j < mm; j++)
{
sig[k, i, j] = 0.0;
}
sig[k, i, i] = 1.0e-10;
}
}
estep();
mstep();
}
public double estep()
{
double[] u = new double[mm];
double[] v = new double[mm];
double oldloglike = loglike;
for (int k = 0; k < kk; k++)
{
//Cholesky choltmp = new Cholesky(sig[k]);
Cholesky choltmp = new Cholesky(Globals.CopyFrom(k, sig));
lndets[k] = choltmp.logdet();
for (int n = 0; n < nn; n++)
{
for (int m = 0; m < mm; m++)
{
u[m] = data[n, m] - means[k, m];
}
choltmp.elsolve(u, v);
double sum = 0.0;
for (int m = 0; m < mm; m++)
{
sum += Globals.SQR(v[m]);
}
resp[n, k] = -0.5 * (sum + lndets[k]) + Math.Log(frac[k]);
}
}
loglike = 0;
for (int n = 0; n < nn; n++)
{
double max = -99.9e99;
for (int k = 0; k < kk; k++)
{
if (resp[n, k] > max)
{
max = resp[n, k];
}
}
double sum = 0.0;
for (int k = 0; k < kk; k++)
{
sum += Math.Exp(resp[n, k] - max);
}
double tmp = max + Math.Log(sum);
for (int k = 0; k < kk; k++)
{
resp[n, k] = Math.Exp(resp[n, k] - tmp);
}
loglike += tmp;
}
return loglike - oldloglike;
}
public void mstep()
{
for (int k = 0; k < kk; k++)
{
double wgt = 0.0;
for (int n = 0; n < nn; n++)
{
wgt += resp[n, k];
}
frac[k] = wgt / nn;
for (int m = 0; m < mm; m++)
{
double sum = 0.0;
for (int n = 0; n < nn; n++)
{
sum += resp[n, k] * data[n, m];
}
means[k, m] = sum / wgt;
for (int j = 0; j < mm; j++)
{
sum = 0.0;
for (int n = 0; n < nn; n++)
{
sum += resp[n, k] * (data[n, m] - means[k, m]) * (data[n, j] - means[k, j]);
}
sig[k, m, j] = sum / wgt;
}
}
}
}
}
}








![2023年中国商业版服务器操作系统市场发展规模分析:未来将保持稳定增长[图]](https://img-blog.csdnimg.cn/img_convert/f2945dd898ffe19816297b0fe41631b1.png)