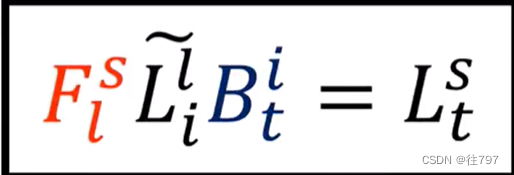线性映射 从一个基底到另一个基底 所遵循的转换规则。
假设: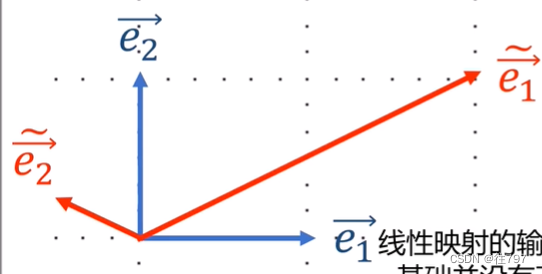
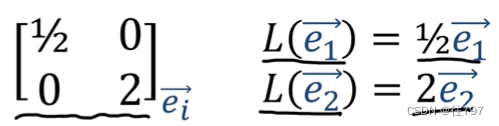
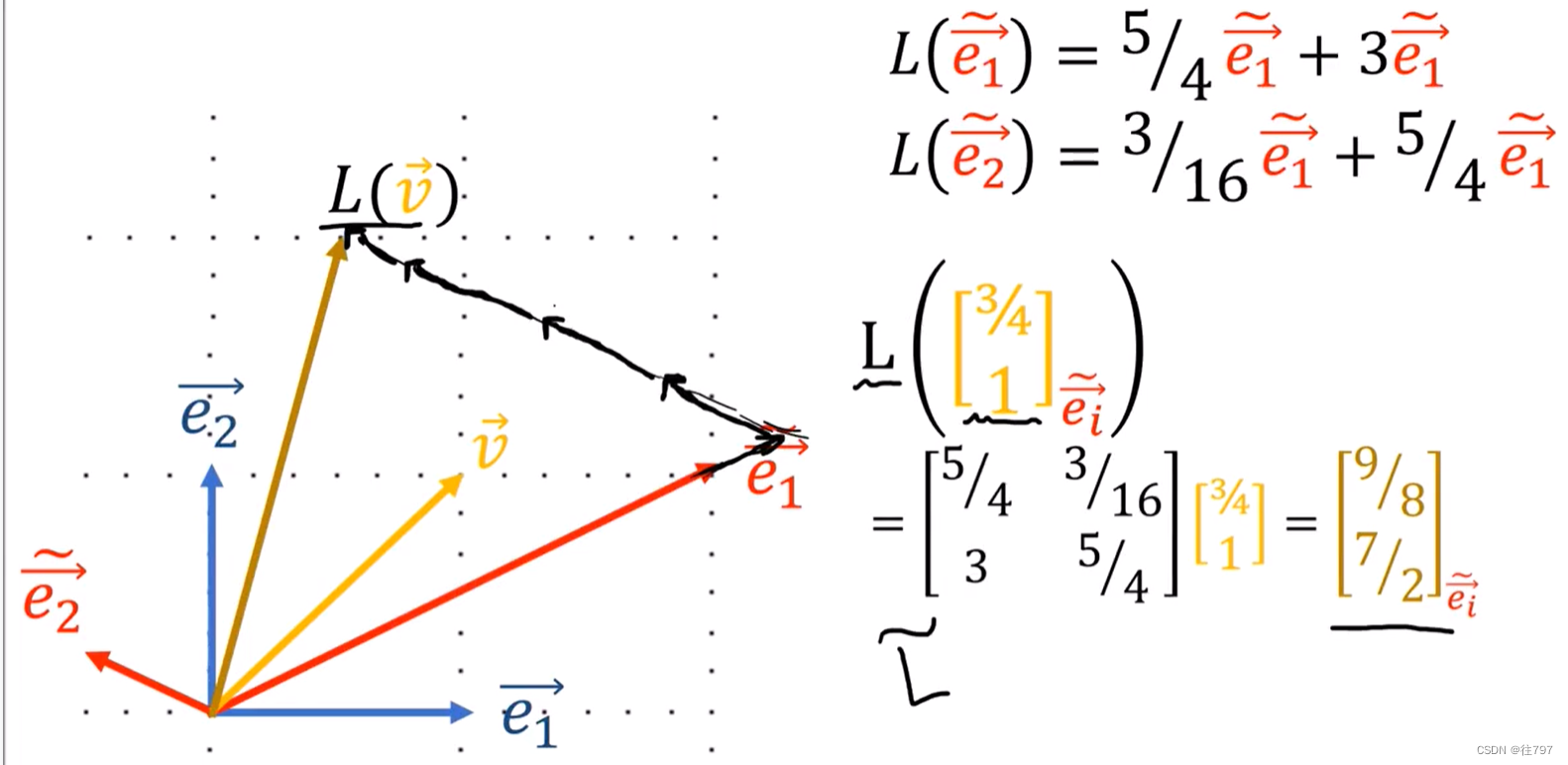
由一个矩阵给出的线性映射在这,并且是在基底e上表示,
该线性映射将e1变成0.5个e1,将e2变成2个e2;
假设有个向量V,其分量是【1,1】,
L将V转换成L(V),
L(V)的分量是什么?-------------------------------只需将V的列向量与L表示的矩阵相乘。
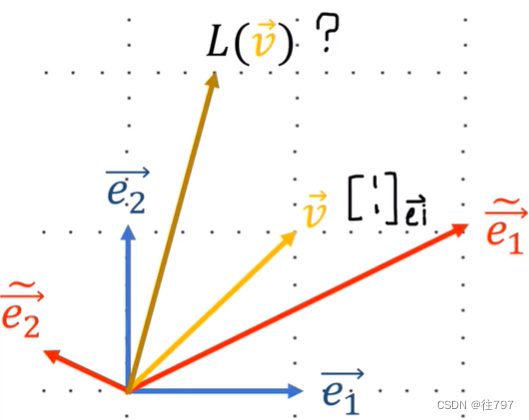
即*
=
所以L(V)的分量是 ,
所有的这些都是在基底e上完成的,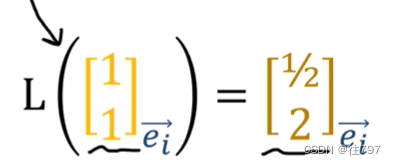
L(V)= 0.5e1 + 2e2
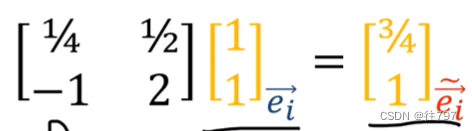
如果把这些在旧基上表示的分量 应用反向变换,可以得到其在新基中的分量,并注意,使用的是反向转换(Backward),因为向量分量是逆变的(contravariant)
在此,可能会问,新基中输出的向量的分量是多少?
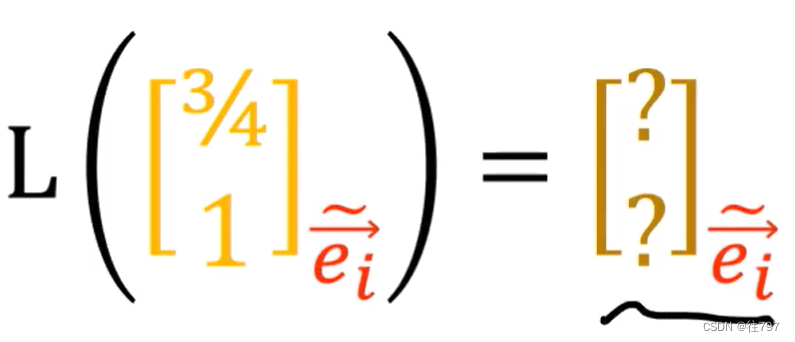
新基中输出的向量的分量是多少?--------这个无法用L所表示的矩阵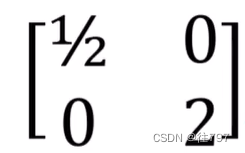 ,因为它只适用于旧基(为什么是这样我也不理解),故需要找到一个新矩阵,这个新矩阵告诉我们如何使用新基
,因为它只适用于旧基(为什么是这样我也不理解),故需要找到一个新矩阵,这个新矩阵告诉我们如何使用新基来构建输出。所以需要计算系数
。
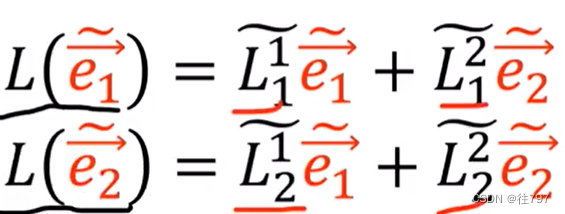
计算如下:
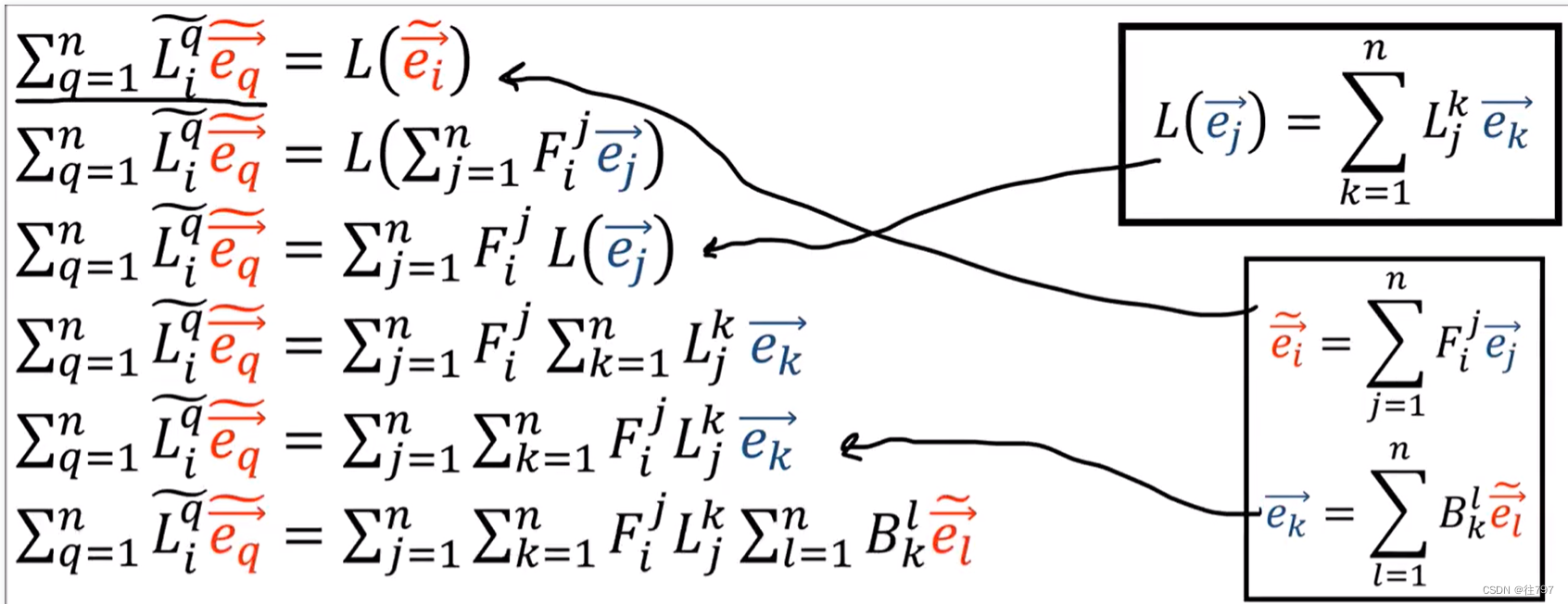
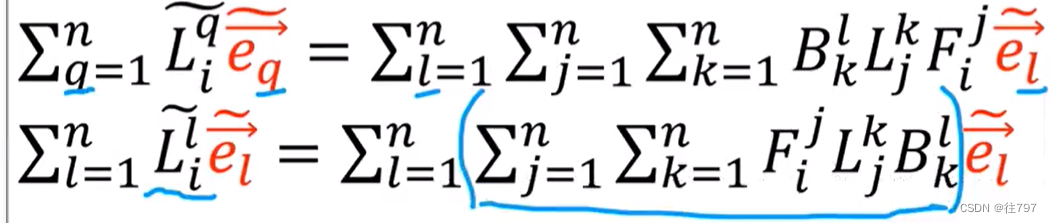
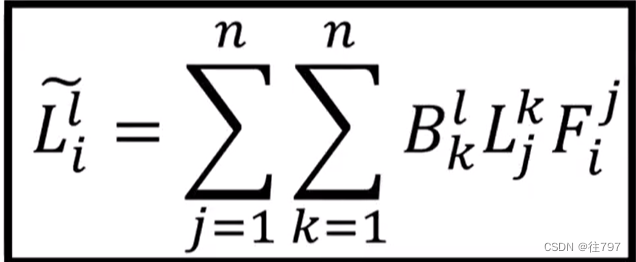
也就是说 要将矩阵坐标从旧基转换到新基,我们要将旧矩阵的左侧乘以后向转换(B),并在旧矩阵的右侧乘以前向转换,。
所以,矩阵或线性映射
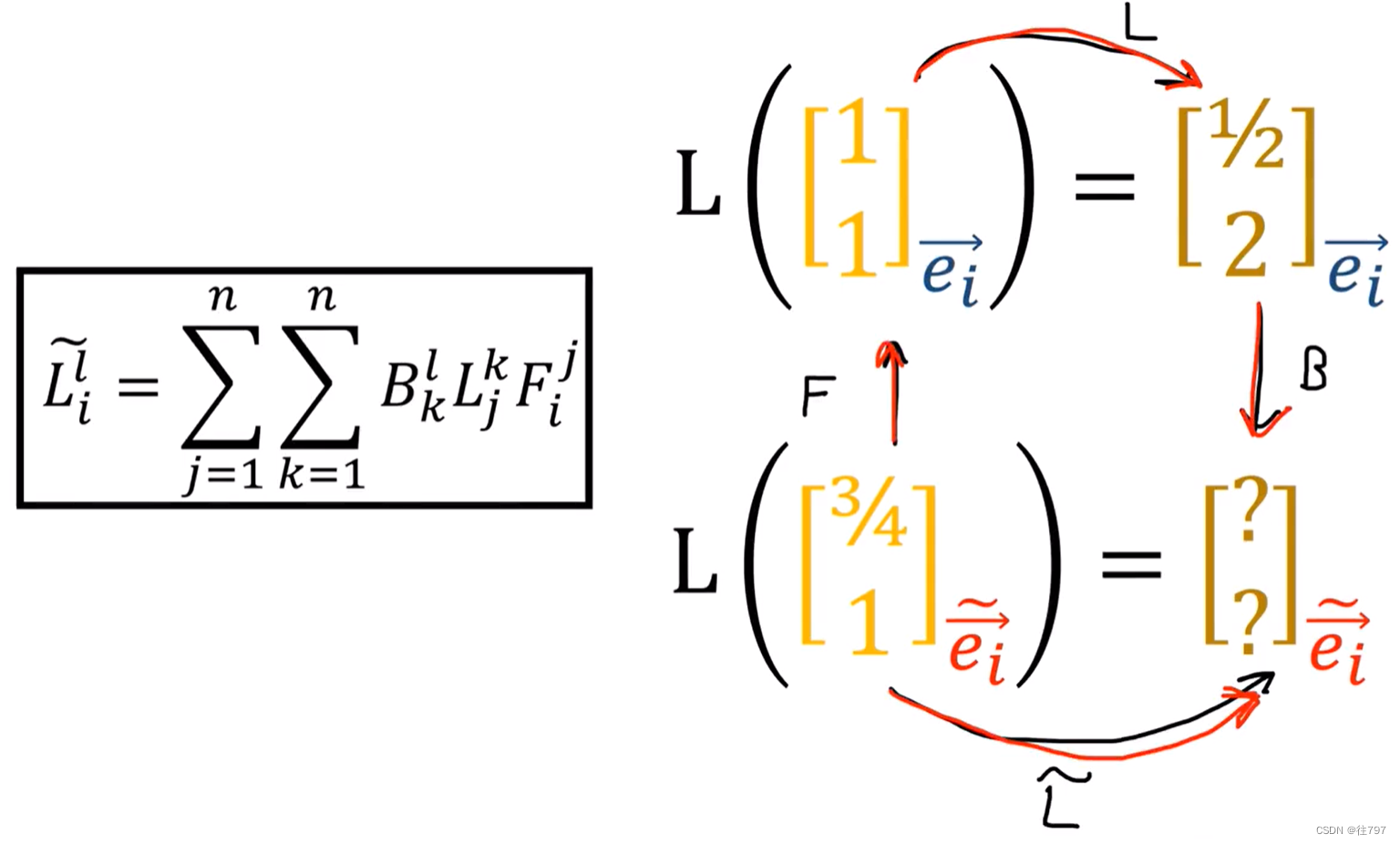
实践
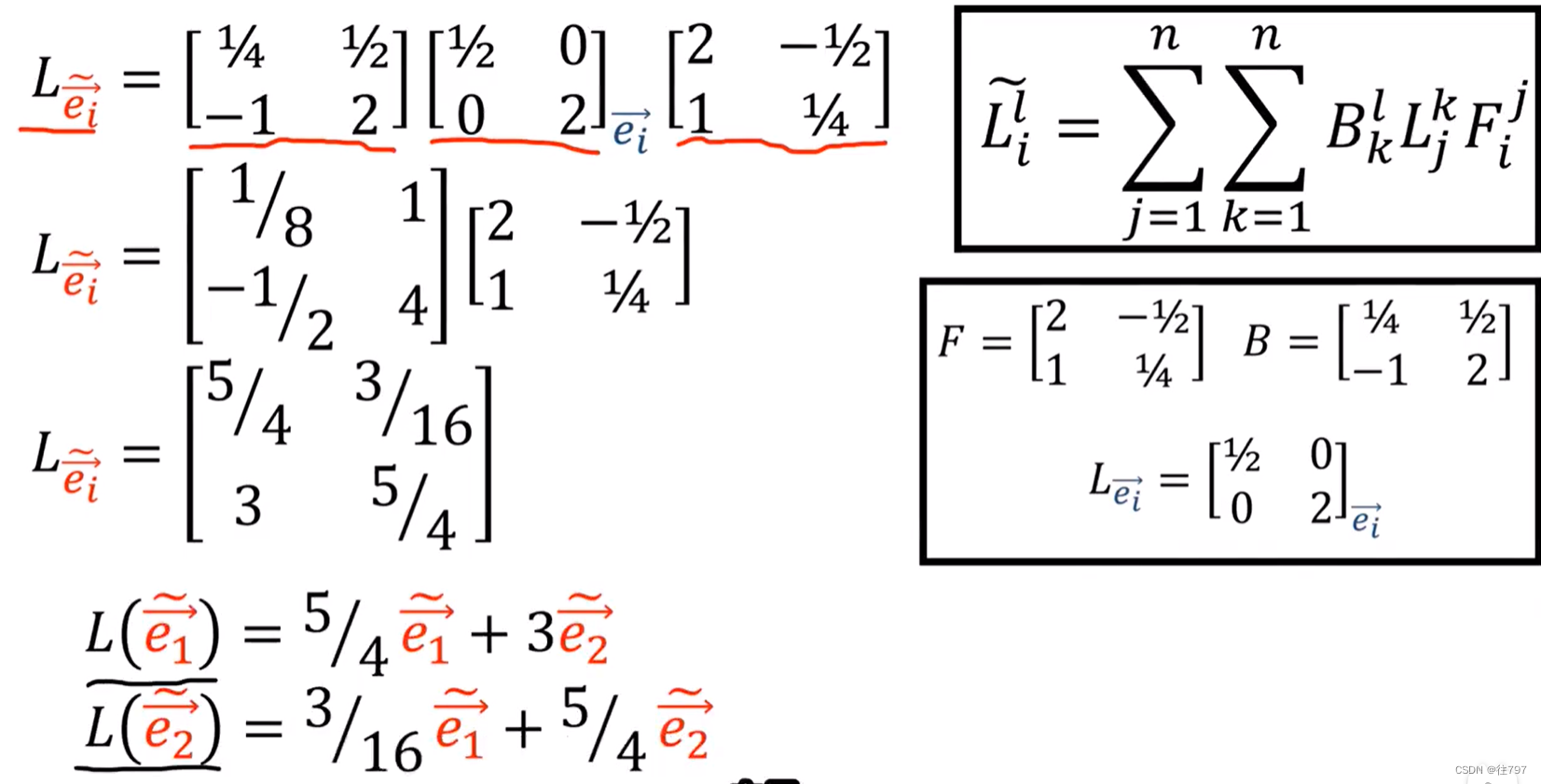
检查是否有效
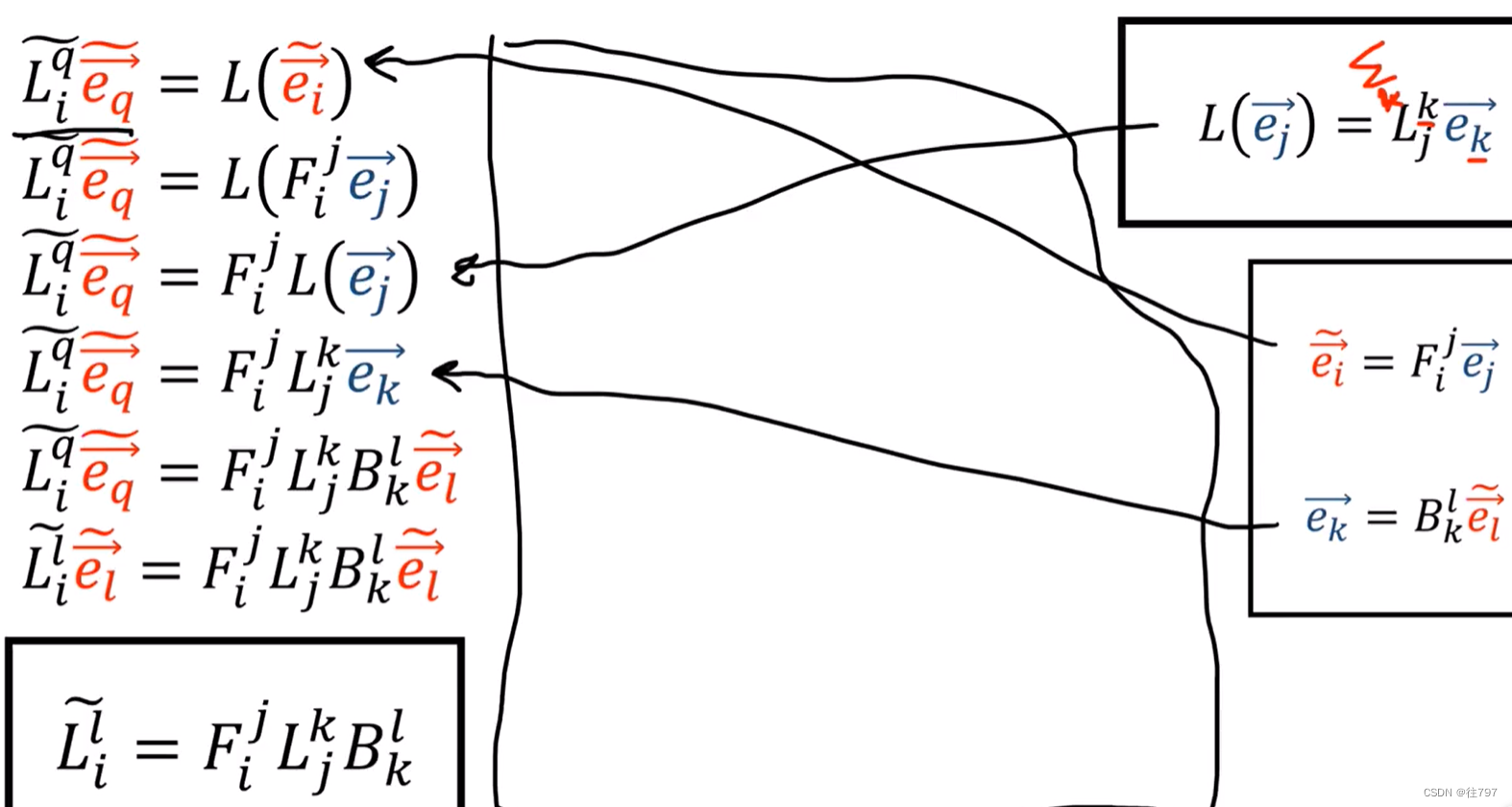
简化上面的推导计算:(技巧1)

观察一下, 发现这些求和的字母符号,有一定规律,其实是可以假装那个求和符号是透明的。
单位矩阵:identity matrix
技巧2:

利用上面两个技巧,来推到矩阵分量的反向转换(Backward) 和 正向转换(Forward)
从旧组件L 移动到 新组件, 只需要
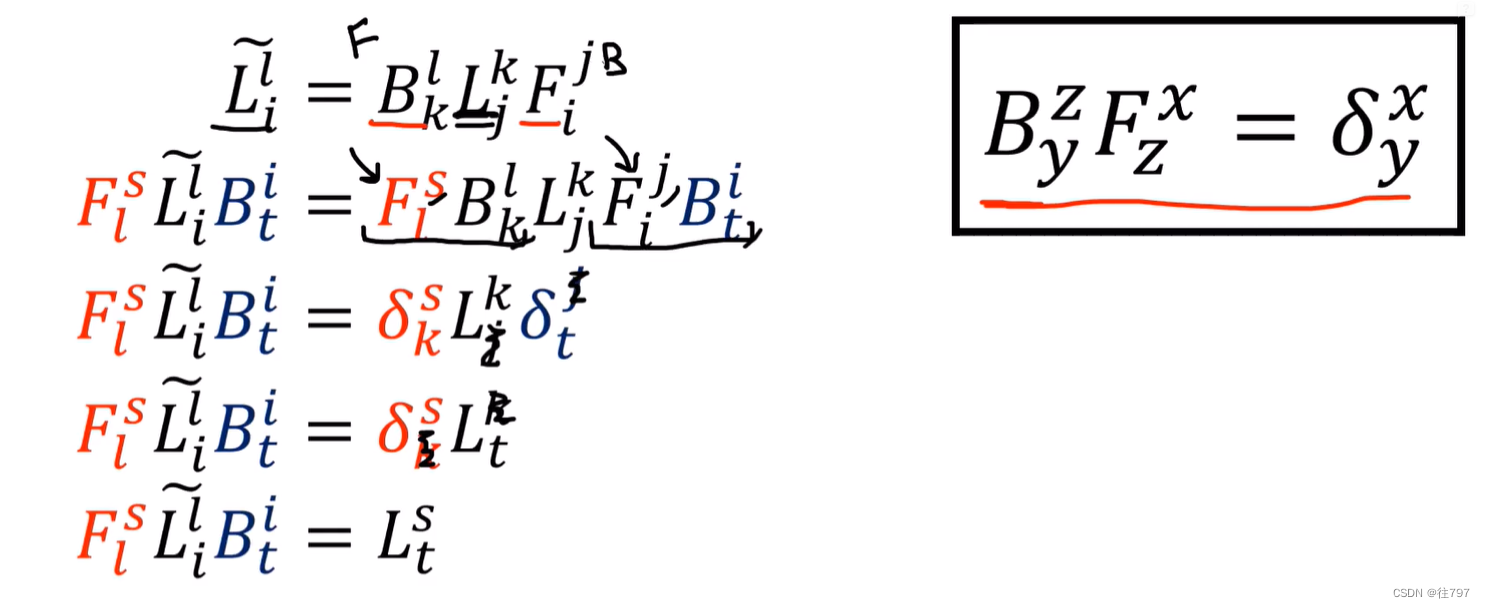
核心内在就是 B与F是互逆的!!