import optimtool as oo
from optimtool.base import np, sp, plt
pip install optimtool>=2.5.0
加载hybird.nesterov.accer方法
import optimtool.hybrid as oh
nes_acc = oh.nesterov.accer
初始化输入数据
f ( x ) = ∑ i = 1 n ( ( n − ∑ j = 1 n cos x j ) + i ( 1 − cos x i ) − sin x i ) 2 , x 0 = [ 0.2 , 0.2 , . . . , 0.2 ] f(x)=\sum_{i=1}^{n}((n-\sum_{j=1}^{n}\cos x_j)+i(1-\cos x_i)-\sin x_i)^2, x_0=[0.2, 0.2, ...,0.2] f(x)=i=1∑n((n−j=1∑ncosxj)+i(1−cosxi)−sinxi)2,x0=[0.2,0.2,...,0.2]
x = sp.symbols("x1:3")
f = (2 - (sp.cos(x[0]) + sp.cos(x[1])) + (1 - sp.cos(x[0])) - sp.sin(x[0]))**2 + \
(2 - (sp.cos(x[0]) + sp.cos(x[1])) + 2 * (1 - sp.cos(x[1])) - sp.sin(x[1]))**2
x_0 = (0.2, 0.2) # Random given
查看复合优化算法的超参数
accer(funcs: FuncArray, args: ArgArray, x_0: PointArray, mu: float=1e-3, proxim: str=“L1”, lk: float=0.01, tk: float=0.02, verbose: bool=False, draw: bool=True, output_f: bool=False, epsilon: float=1e-6, k: int=0) -> OutputType
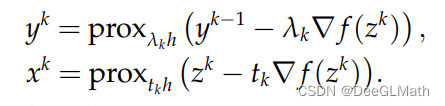
λ
k
\lambda_k
λk为算法中的lk,
t
k
t_k
tk为算法中的tk,
p
r
o
x
\mathrm{prox}
prox算符的含义见如何研究带有不可微项的目标函数的局部极小值?。
调用并绘制迭代图
print(nes_acc(f, x, x_0, verbose=True, lk=0.1, tk=0.2))
# ensure lk and tk < 1 / L (L comes from lipschitz continuity condition)
默认的lk和tk能够解决稀疏矩阵解的问题,在实际问题中可以适当增大。
(0.2, 0.2) 0.033830304000793295 0
[0.19256431 0.19256431] 0.03265408936657944 1
[0.18638465 0.18638465] 0.031617693847704915 2
[0.17987066 0.17987066] 0.03047115719116562 3
[0.1730253 0.1730253] 0.029210872201568115 4
[0.16579189 0.16579189] 0.027822939438030186 5
[0.1581071 0.1581071] 0.02629215385584641 6
[0.14993051 0.14993051] 0.024608804452366514 7
[0.1412556 0.1412556] 0.02277288945465011 8
[0.13211227 0.13211227] 0.020796735113812578 9
[0.12256644 0.12256644] 0.018706522868828408 10
[0.11271834 0.11271834] 0.01654250102784132 11
[0.10269905 0.10269905] 0.014357303201991972 12
[0.09266423 0.09266423] 0.012211920332773922 13
[0.08278452 0.08278452] 0.01016943425860308 14
[0.07323288 0.07323288] 0.008287438822270246 15
[0.0641702 0.0641702] 0.006610792391354569 16
[0.05573159 0.05573159] 0.005166538950867488 17
[0.04801584 0.04801584] 0.003962275998264823 18
[0.04108007 0.04108007] 0.0029881260918894485 19
[0.03494014 0.03494014] 0.0022213296681673307 20
[0.0295762 0.0295762] 0.0016318641094921836 21
[0.02494136 0.02494136] 0.0011875956332260999 22
[0.02097132 0.02097132] 0.0008580603239475022 23
[0.01759323 0.01759323] 0.000616649225758882 24
[0.01473264 0.01473264] 0.0004414466868771702 25
[0.0123183 0.0123183] 0.0003151622104264512 26
[0.01028495 0.01028495] 0.0002245773826627801 27
[0.00857464 0.00857464] 0.00015981543713860277 28
[0.00713697 0.00713697] 0.00011361642729667025 29
[0.00592872 0.00592872] 8.070513699807076e-05 30
[0.00491322 0.00491322] 5.727893092786287e-05 31
[0.00405951 0.00405951] 4.061141417882402e-05 32
[0.00334156 0.00334156] 2.875475343419944e-05 33
[0.00273758 0.00273758] 2.032048717223606e-05 34
[0.00222925 0.00222925] 1.4320242141885246e-05 35
[0.00180129 0.00180129] 1.0050987097603078e-05 36
[0.00144084 0.00144084] 7.012839175347395e-06 37
[0.00113718 0.00113718] 4.85040116210444e-06 38
[0.00088126 0.00088126] 3.3109866323555416e-06 39
[0.00066554 0.00066554] 2.214909990704722e-06 40
[0.00048366 0.00048366] 1.434371414320055e-06 41
[0.00033027 0.00033027] 8.784544440346822e-07 42
[0.0002009 0.0002009] 4.82466914247575e-07 43
[9.1765239e-05 9.1765239e-05] 2.003667873131081e-07 44
[-3.10652223e-07 -3.10652223e-07] 6.2149745663463e-10 45
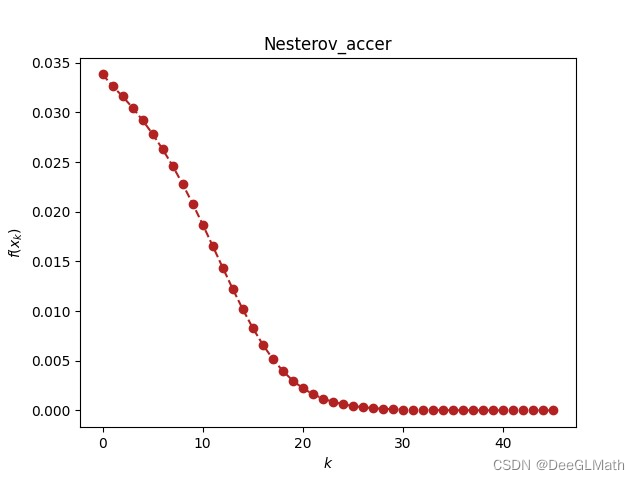
当
f
f
f为非凸函数时,算法也收敛。