赔率与概率不同

Odds != Probability

许多人将“赔率”和“概率”这两个词混为一谈。它们都表示对可能性或机会的估计。我可以理解普通人这样做，但我经常看到数据科学家和统计学家也混淆了这些概念，这是一种遗憾，因为在数学上它们有不同的含义。

尽管它们相关，但赔率和概率在尺度和含义上有很大的不同。当在错误的背景下混淆时，这可能导致对机会的错误估计，从而导致错误的决策。

在本文中，我想说明这些差异是什么，以及在混淆这两者时，如何真正影响分析和研究。

概率和赔率之间有什么区别？

Probability vs odds

想象一下，你把手伸进一个黑色的袋子。在那个袋子里有五个红球，三个蓝球和两个黄球。

概率被定义为某一事件发生的次数，表示为所有可能发生事件的比例。在我们的黑色袋子中有三个蓝球，但总共有十个球，所以你拿出一个蓝球的概率是三除以十，即30%或0.3。

赔率被定义为某一事件发生的次数 / 为该事件不发生的次数的比例。

在我们的黑袋中有三个蓝球，但有七个不是蓝色的球，所以抽出一个蓝球的赔率是3:7。

赔率通常表示为“odds”，在这种情况下是三除以七，约为43%或0.43，或表示为“赔率赔率”，在这种情况下是七除以三，即233%或2.33。

如何赔率与概率有关？

在赔率和概率之间进行转换并不难，以下是两个简单的转换公式，看看你是否能理解为什么这些公式是如何根据我上面提供的简单例子工作的：

如果某事发生的概率是P，那么它发生的赔率是P/(1-P)。

参见图1，了解更多信息。

如果某事发生的赔率是O，那么它发生的概率是O/(1+O)。

想想赔率和概率在属性上的不同也是有帮助的：

概率的范围是从零到一。赔率的范围是无穷大。

某事发生的概率总是小于它发生的赔率（假设概率不为零）。

概率越小，概率和赔率越相似。例如，赢得英国国家彩票的概率为0.0000000221938762。赔率是0.0000000221938767。

概率越大，赔率与概率之间的差异越大。高概率对应着天文数字的赔率。90%的概率等于900%的赔率，99%等于9,900%的赔率，99.999%等于9,999,900%的赔率。

为什么这很重要？

这可能会导致对理解造成重大错误的领域之一是在研究问题时使用逻辑回归。逻辑回归用于模拟某些输入变量可能如何影响二元（或多类）结果（例如，是或否，组成员或非组成员）。

例如，可以使用逻辑回归来确定一系列生活方式因素如何影响某种疾病的五年存活结果。

逻辑回归模型使用赔率比来量化给定输入变量的影响程度。赔率比描述了基于输入变量的一单位增加而发生的结果赔率的百分比变化。

例如，你可能计算出个体每增加一千克体重，患某种疾病的赔率就增加5%。

这并不意味着“每增加一千克体重，患病的概率增加5%”。

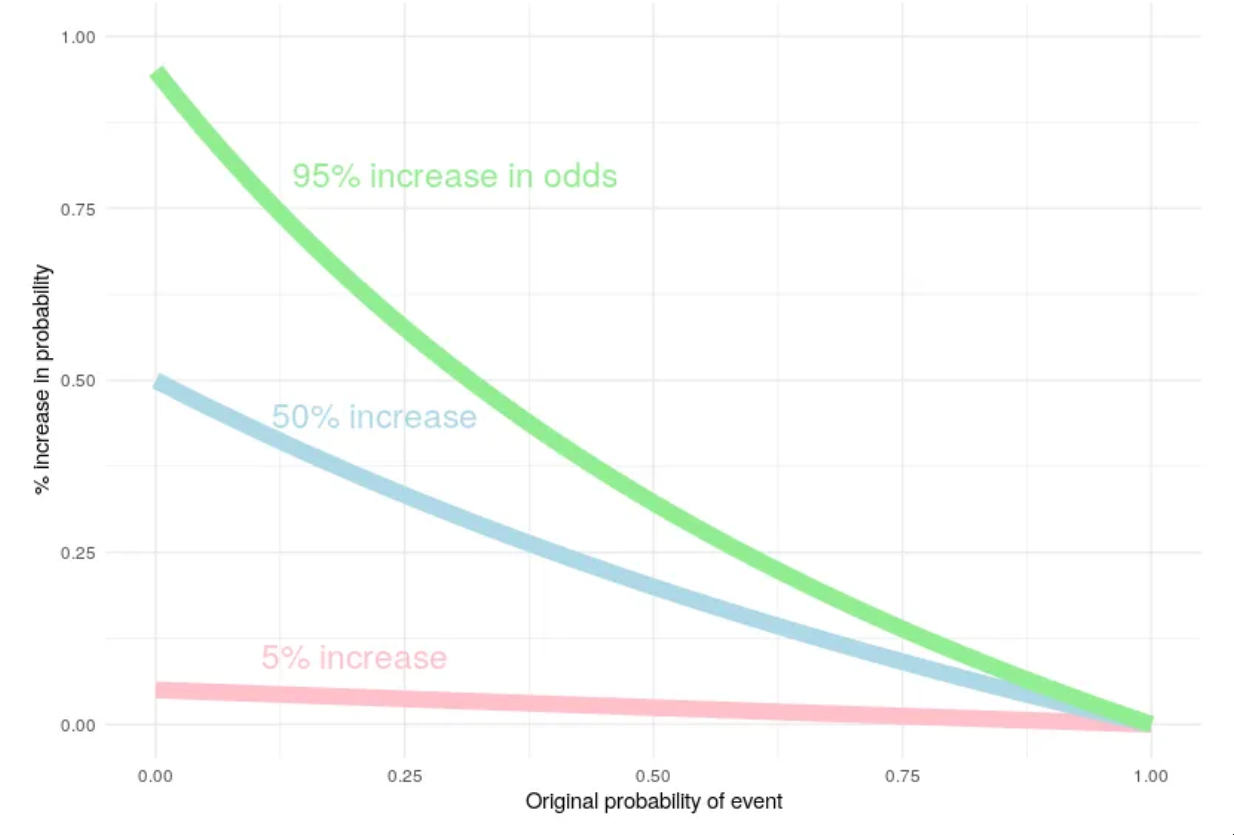
这取决于首次发病的概率是多少。根据事件的先验概率，赔率增加的影响会减小。图2说明了这一点。

要注意的主要事项是，在量化变量的影响时不要混淆赔率和概率。一般来说（除了完全确定或完全不可能的情况），增加的赔率意味着增加的概率-通常使用术语“可能性”来同时涵盖它们两个。

因此，当谈论方向性效应时，通常可以安全地将这些术语视为同义词。当你在量化这些效应时，你必须仔细掌握你的语言。

我最初是一名纯数学家，后来成为了心理测量学家和数据科学家。我热衷于将所有这些学科的严密性应用于复杂的人类问题。