本文总结参考于 kira 2023概率提神醒脑技巧班。
笔记均为自用整理。加油!ヾ(◍°∇°◍)ノ゙
第一部分笔记详见
概率 | 【提神醒脑】自用笔记串联一 —— 事件、随机变量及其分布_西皮呦的博客-CSDN博客
一研为定!
四、随机变量的数字特征
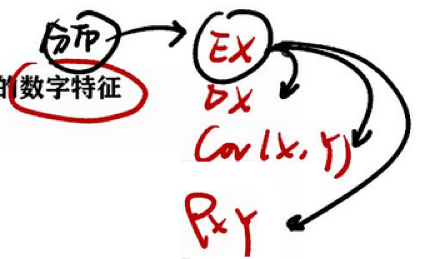
4.1、数学期望(先判X、Y的类型)
- 辨析:
- 1、
- 2、期望指的是 f 是谁的函数。
- 所有的随机变量都有数学期望吗?
- —— 错误,前提是要绝对收敛。
- —— 可与第五章 大数定律、切比雪夫结合出题。
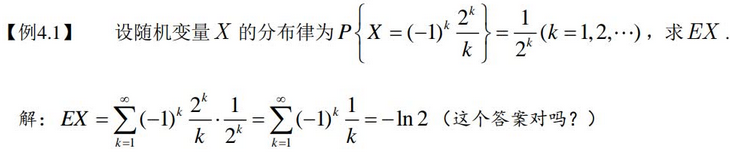
- 错误。EX 不存在。
- 唯独需要考虑,级数中的条件收敛。

若X是离散型,Y一定是离散型。但是若X是连续型,Y不一定是连续型。必须严格单调。
- 系数往外提,和差都能拆
---------------------------------------------------------------------------------------------------------------------------------
【例4.2】应用题【已知X分布,求EY】
① 找X分布 ②Y=g(X)函数



- 期望和方差都是一维的。
---------------------------------------------------------------------------------------------------------------------------------
【例4.2】

【解析】
连续型直接积分。

4.2、方差
---------------------------------------------------------------------------------------------------------------------------------
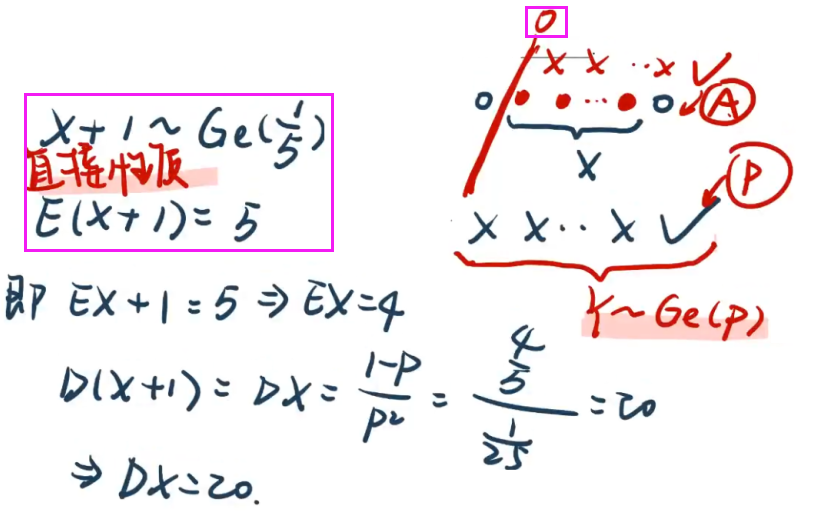
【例4.4】 几何分布、直接利用分布的性质而不用概率密度积分



![]()
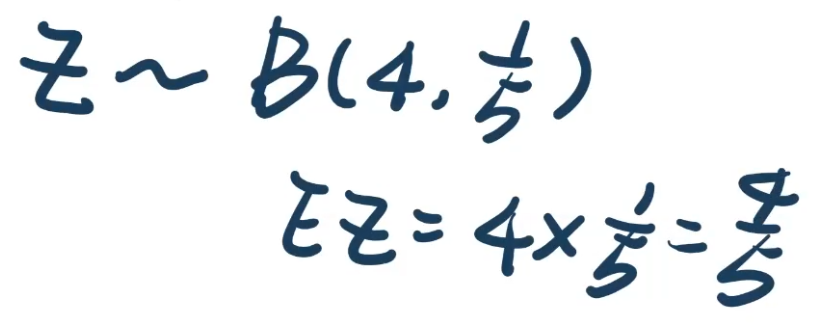
---------------------------------------------------------------------------------------------------------------------------------
【例4.5】
![]()
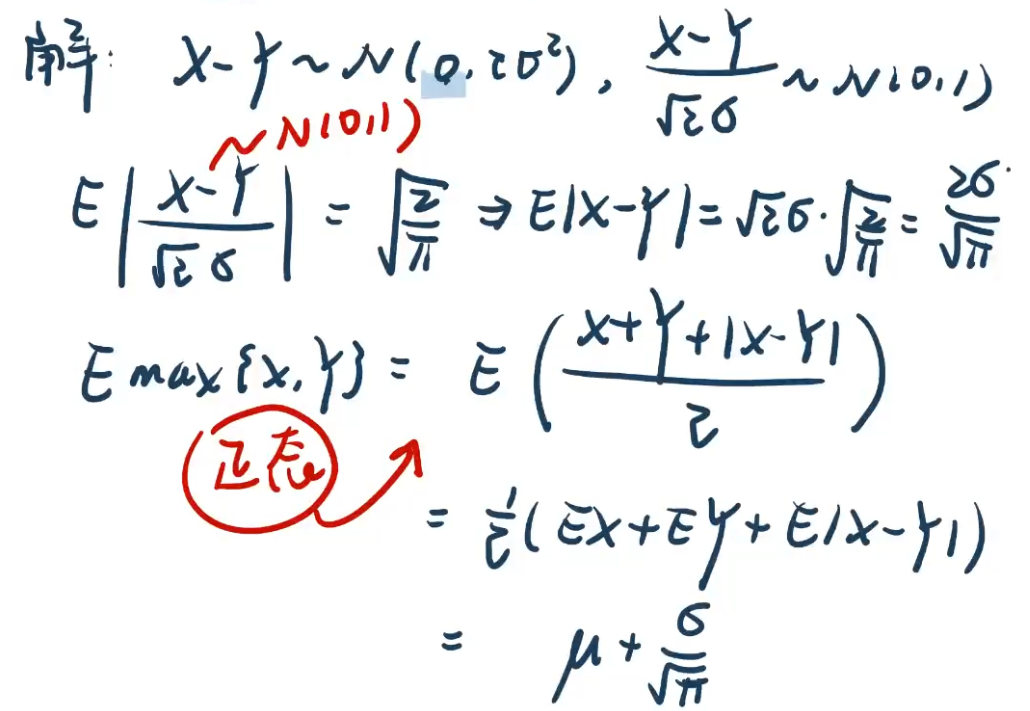
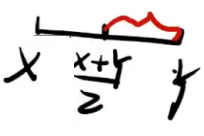
※☆☺最大最小值期望
 ;若括号里是1,则为最小值。
;若括号里是1,则为最小值。
【例4.6】一般连续型随机变量求期望 → 转一维



第二问利用 ——

4.3、随机变量的矩、协方差和相关系数
---------------------------------------------------------------------------------------------------------------------------------
【例4.7】

【解析】A
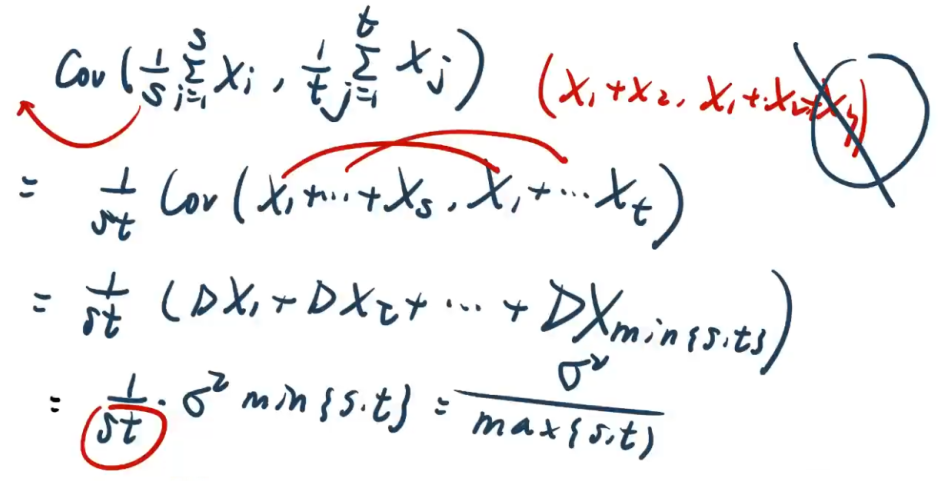
---------------------------------------------------------------------------------------------------------------------------------
【例4.8】


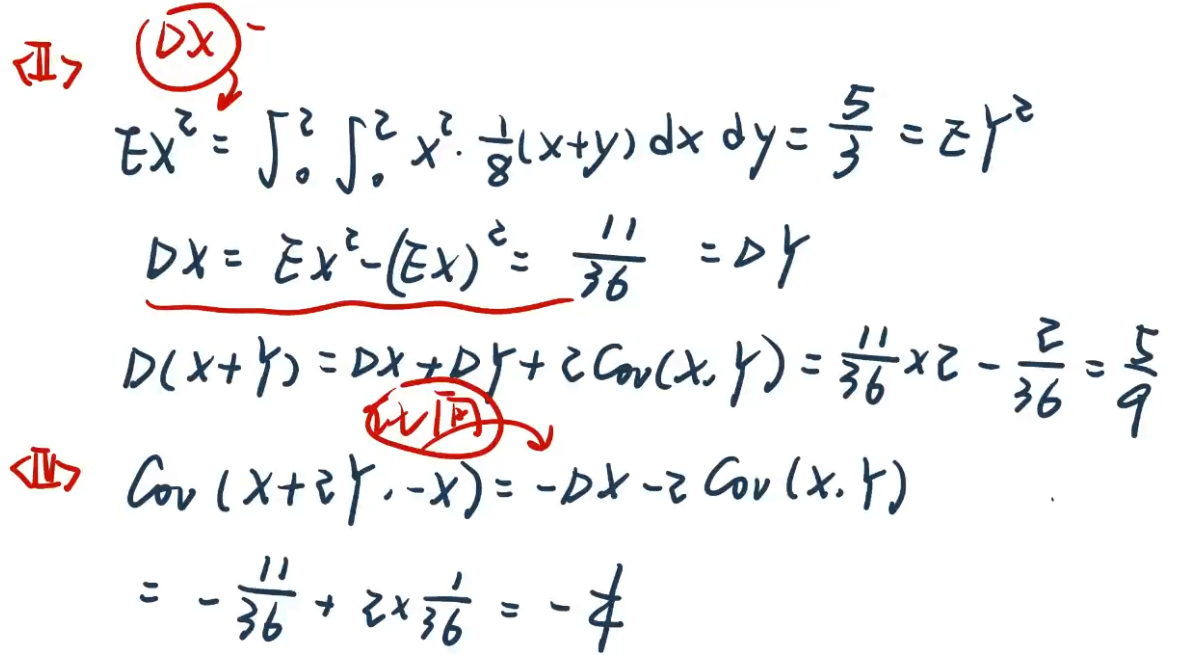
4.3、相关系数
---------------------------------------------------------------------------------------------------------------------------------
※☆☺线性相关系数不是看斜率!

【例4.9】
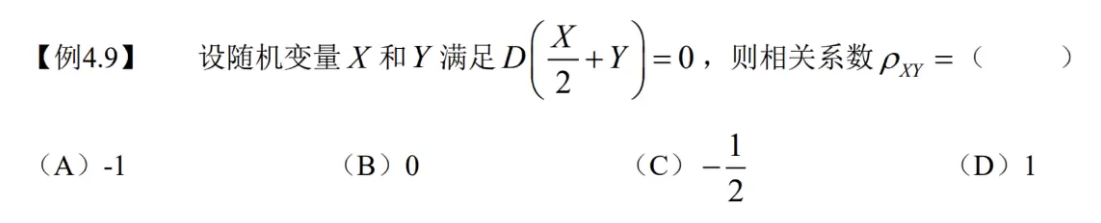
【解析】A
不是看斜率!
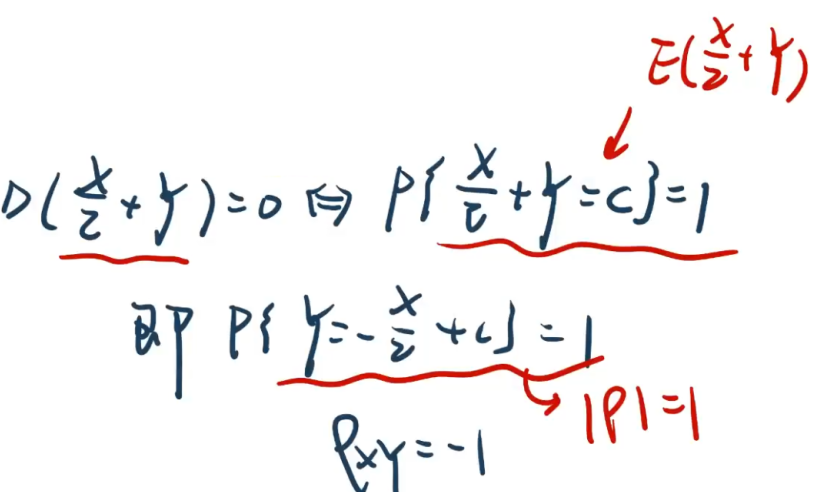
4.4、四个等价命题

- X,Y不相关一定独立,X,Y独立不一定不相关。
- 二维正态 变 五个等价命题。+ 独立
---------------------------------------------------------------------------------------------------------------------------------
※☆☺ 0-x分布 概率与期望互推
【例4.11】

※ ※ ※ 二维正态分布

- X和Y都服从一维正态分布,请问aX+bY(ab≠0)服从什么分布? —— 不一定
- 如果再添加一个条件“X和Y独立”呢? —— 正态
---------------------------------------------------------------------------------------------------------------------------------
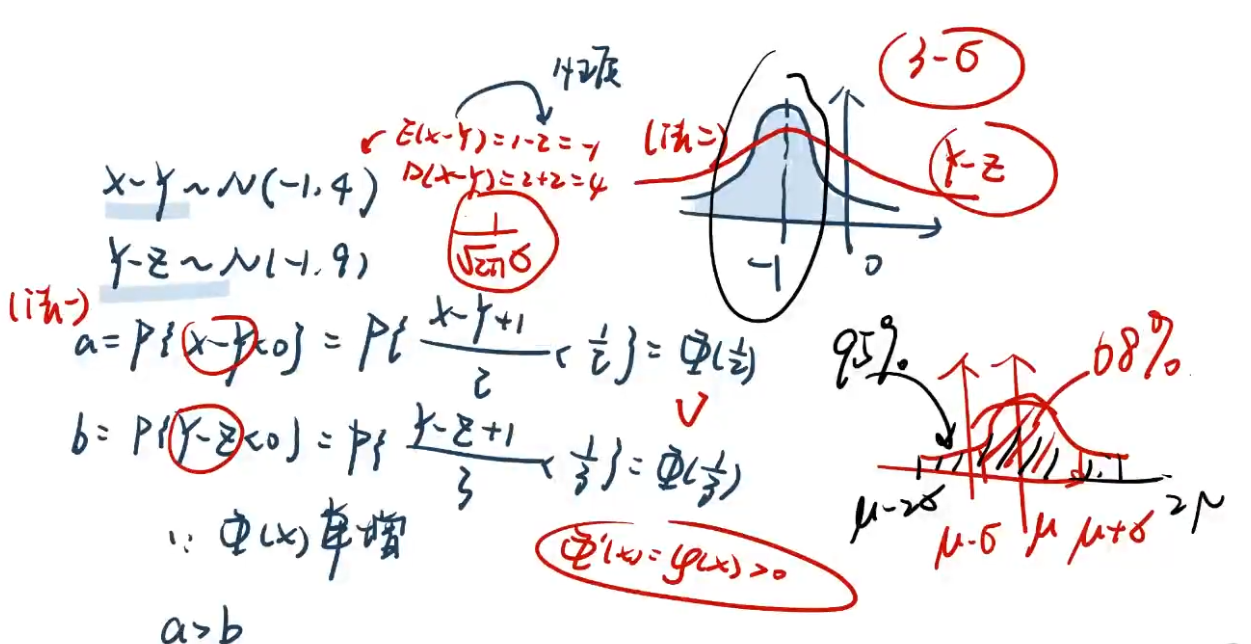
【例3.9】

【解析】
法一可以用 大φ 求导
---------------------------------------------------------------------------------------------------------------------------------
【例3.10】



---------------------------------------------------------------------------------------------------------------------------------
【2022 数一】

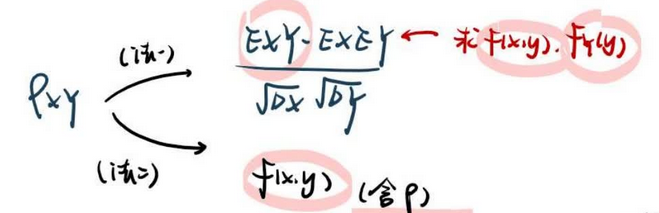
法一:对比 背诵公式
法二:正常积分求,注意 条件概率密度的使用,X当常数!


五、大数定律与中心极限定理
5.1、切比雪夫不等式
---------------------------------------------------------------------------------------------------------------------------------
【例5.1】

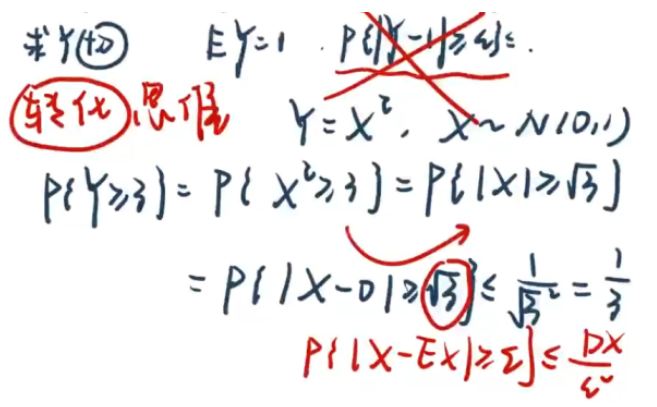
5.2、大数定律
5.2.1、依概率收敛


5.2.2、切比雪夫大数定律(三个条件)
5.2.3、辛钦大数定律(两个条件)

- 求谁的平均,验谁的条件。
【例5.2】


---------------------------------------------------------------------------------------------------------------------------------
【例5.3】


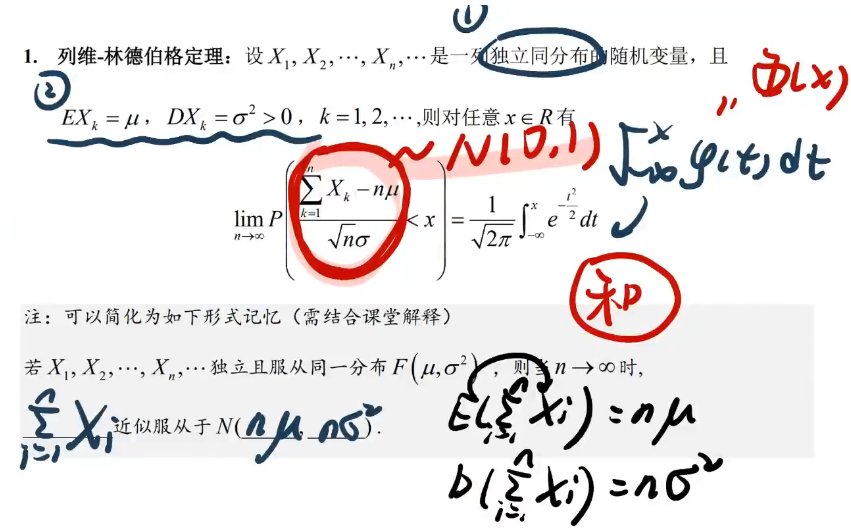
5.3、中心极限定理 【研究和的分布、次数的分布】
---------------------------------------------------------------------------------------------------------------------------------
【例5.4】求谁的和就设谁是xi

 ---------------------------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------------------------------
【例5.5】

【解析】A
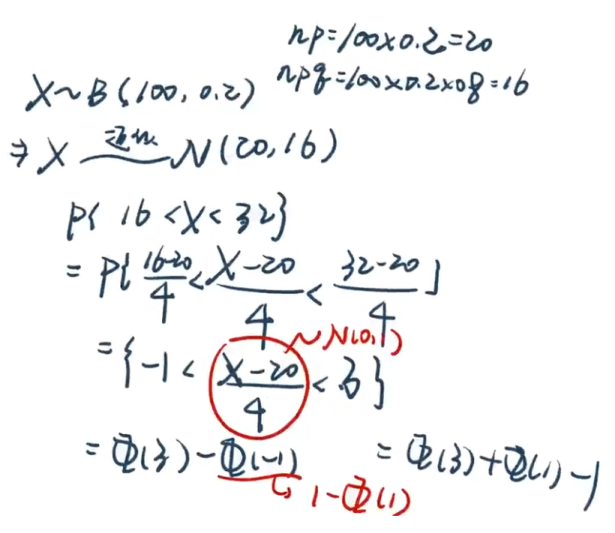
六、数理统计【背公式 求你了】

6.1、统计量与统计值
- 样本:相互独立且和总体同分布的随机变量。
---------------------------------------------------------------------------------------------------------------------------------
【例6.6】

---------------------------------------------------------------------------------------------------------------------------------
【例6.1】


---------------------------------------------------------------------------------------------------------------------------------
【例6.2】统计量的数字特征
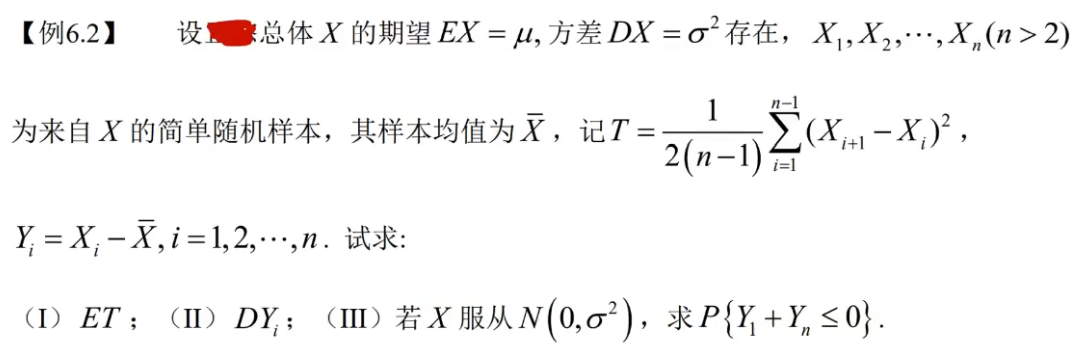
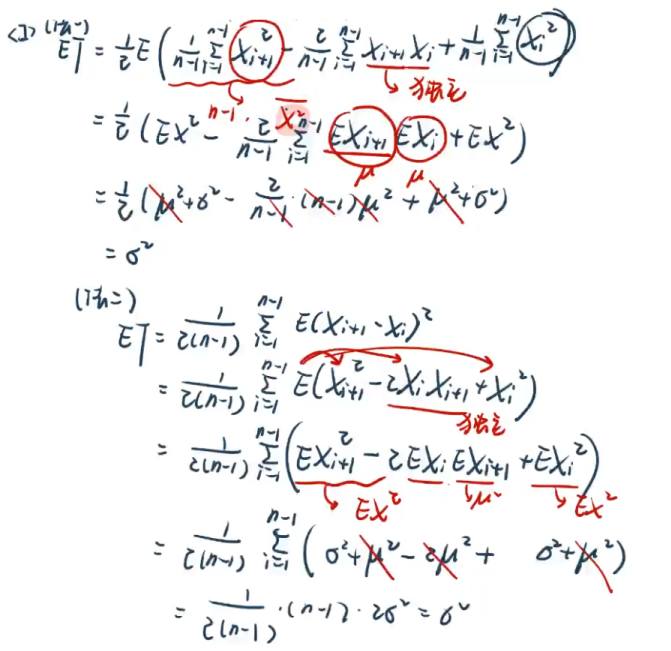
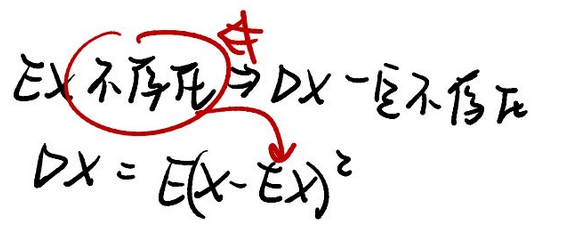

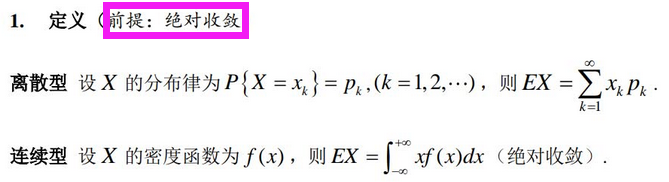




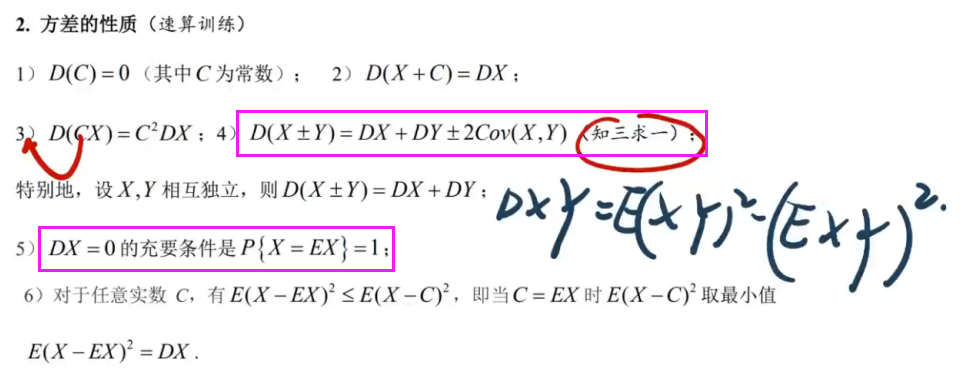





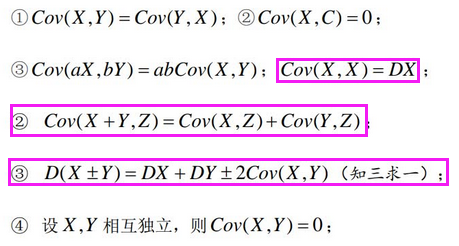



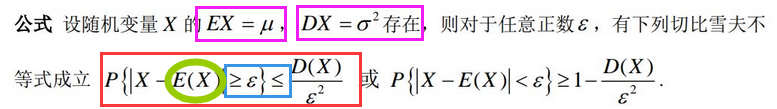







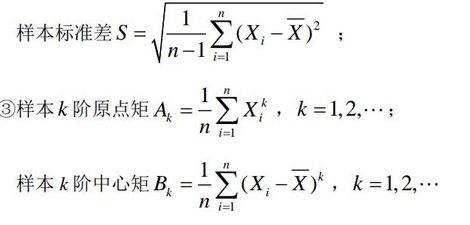

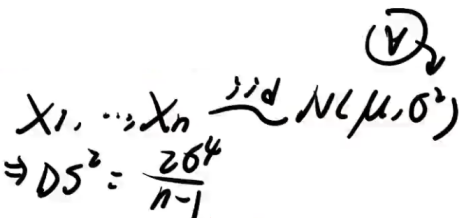
![[附源码]java毕业设计基于学生信息管理系统](https://img-blog.csdnimg.cn/35e84dc086914025a51641038857d45f.png)
及结构体长度及占用空间的一些特性说明和测试](https://img-blog.csdnimg.cn/c58c0b8685fc4747aab6b85993271712.png)