题目
给定一个未排序的整数数组,找到最长递增子序列的个数。
示例 1:
输入: [1,3,5,4,7] 输出: 2 解释: 有两个最长递增子序列,分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。
示例 2:输入: [2,2,2,2,2] 输出: 5 解释: 最长递增子序列的长度是1,并且存在5个子序列的长度为1,因此输出5。
思路
本题相当于是最长上升子序列的进阶版本
动规五部曲:
- 确定dp数组和下标含义
本题要求最长递增子序列的个数,所以要维护两个数组
dp[i]:i之前(包括i)最长递增子序列的长度为dp[i]
count[i]:以nums[i]结尾的字符串,最长递增子序列的个数为count[i] - 确定递推公式
在最长上升子序列中,给出的状态转移为:
if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
即:位置i的最长递增子序列长度 等于j从0到i-1各个位置的最长升序子序列 + 1的最大值
而在本题中,要维护两个维度,一个是dp[i],一个是count[i]
count[i]记录了以nums[i]为结尾的字符串,最长递增子序列的个数
dp[i]记录了i之前(包括i)最长递增序列的长度
对于count[i]:
在nums[i] > nums[j]前提下:
(1)如果在[0, i-1]的范围内,找到了j,使得dp[j] + 1 > dp[i],说明j的位置找到了一个比i位置更长的递增子序列(j < i),那么以j为结尾的子串的最长递增子序列的个数,就是最新的以i为结尾的子串的最长递增子序列的个数,即:count[i] = count[j](因为长短不一选最长)
(2)如果在[0, i-1]的范围内,找到了j,使得dp[j] + 1 == dp[i],说明在位置j和位置i找到了两个相同长度的递增子序列,即count[i] += count[j](因为两者相同同时累计)
- 初始化dp数组
count[i]记录了以nums[i]为结尾的字符串,最长递增子序列的个数,最少也就是1个,所以count[i]初始为1
dp[i]记录了i之前(包括i)最长递增序列的长度,最小的长度也是1,所以dp[i]初始为1
- 确定遍历顺序
dp[i]是由0到i-1各个位置的最长升序子序列 推导而来,那么遍历i一定是从前向后遍历。
j其实就是0到i-1,遍历i的循环在外层,遍历j则在内层
- 举例推导dp数组
输入:[1,3,5,4,7]
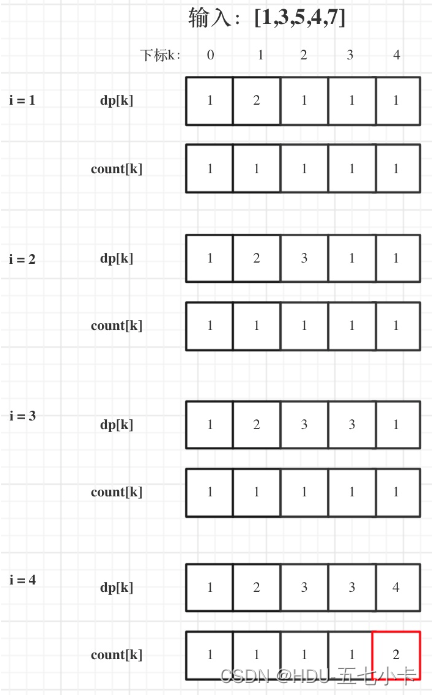
java代码如下:
class Solution {
public int findNumberOfLIS(int[] nums){
if(nums.length <= 1) return nums.length;
int[] dp = new int[nums.length];
for(int i = 0; i < nums.length; i++){
dp[i] = 1;//最小长度为1,初始化为1
}
int[] count = new int[nums.length];
for(int i = 0; i < nums.length; i++){
count[i] = 1;//最少个数也是1,初始化为1
}
int maxCount = 0;
for(int i = 1; i < nums.length; i++){
for(int j = 0; j < i; j++){//注意开始条件,相当于是j=0和i=1开始比较
if(nums[i] > nums[j]){
if(dp[j] + 1 > dp[i]){//说明找到了一个更长的上升子序列
dp[i] = dp[j] + 1;//更新dp[i]
count[i] = count[j];//更新个数
} else if(dp[j] + 1 == dp[i]){//说明找到了链各个相同长度的最长上升子序列
count[i] += count[j];//相同长度的话就是累加
}
}
if(dp[i] > maxCount){
maxCount = dp[i];//更新最长上升子序列的长度
}
}
}
//两层for之后,dp[i]存储了i之前的最长上升子序列的长度,count[i]存储了以nums[i]结尾的最长上升子序列的个数
//遍历dp[i],只要发现一个最长上升子序列,则统计对应的count[i]并累加到结果中去
int result = 0;//统计个数
for(int i = 0; i < nums.length; i++){
if(maxCount == dp[i]){
result += count[i];
}
}
return result;
}
}