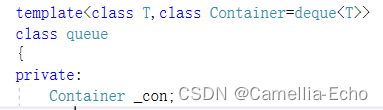
一、导数

  导数是描述函数变化率的数学概念。

 

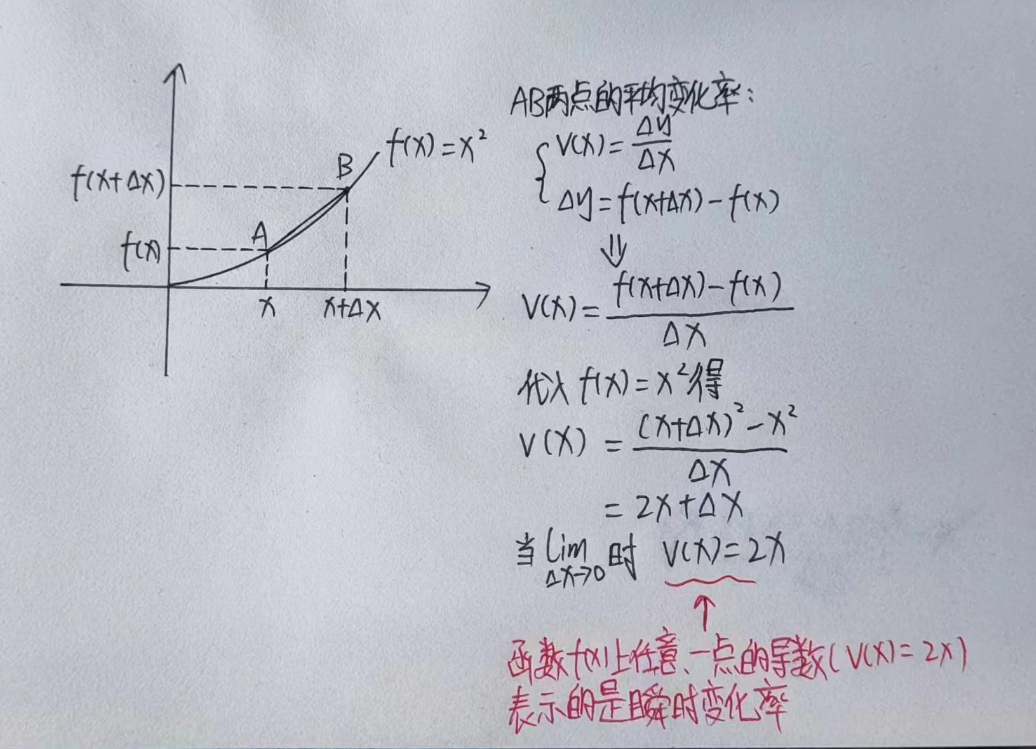
 导数的定义式: 

 

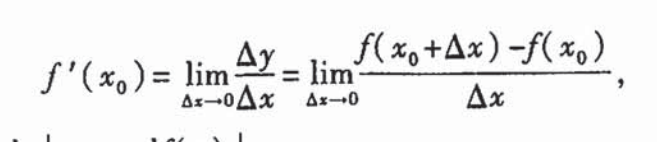
那么就有一个问题，为什么求函数的最大值点是要对其自变量求导，并使其导数等于0

比如:求L(θ)=3lnθ+2ln(1-θ)的最大值点

 

既然导数表示函数的变化率，那么当函数L(θ)的导数等于0，也就是函数L(θ)的变化率等于0，函数不再变化了，这个值唯一了，那么唯一的值只可能是最大值或最小值。

二、偏导数 

偏导数描述了函数沿着某个特定方向的变化率。

导数是用来研究一元函数的变化率，对于多元函数的变化率，先研究多元函数中一个自变量的变化率，称为偏导数。

偏导数定义式: 

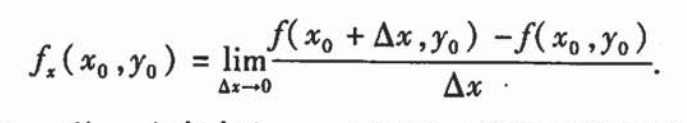
当然上述定义式是对x求偏导。对于多元函数，例如f(x,y)=x^2+y^2之类的，我们要研究对一个自变量求导，比如x方向，那么另一个自变量y就不能改变，这是规定的。

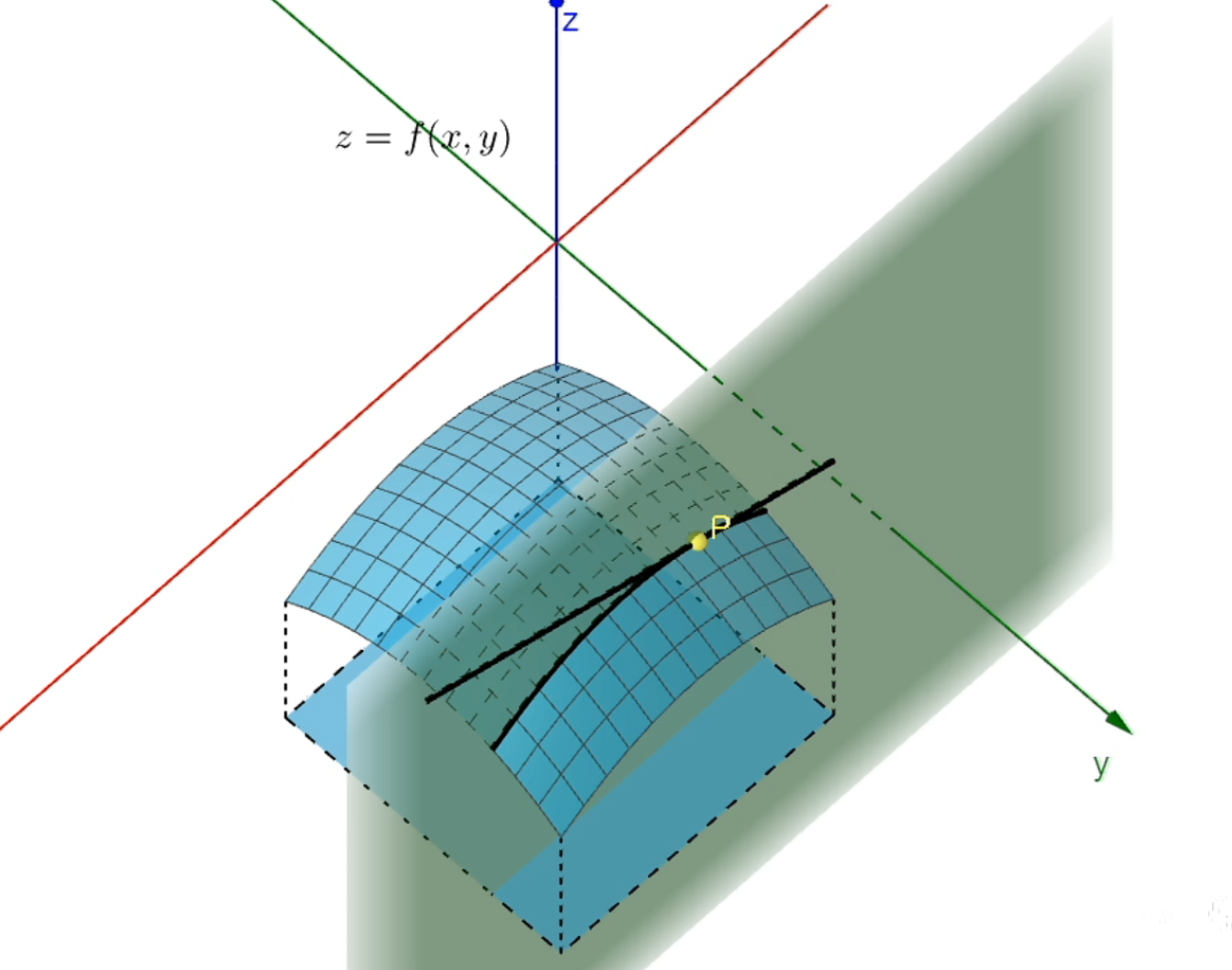
偏导数是求函数在某一点上x方向或y方向上的变化率，如果要求函数在x方向上的变化率，那么自变量y就不能变化，反之亦然。 

三、方向导数

导数描述一元函数的变化率，偏导数描述多元函数在自变量方向上的变化率，方向导数更进一步，从名字中可以看出，“方向”，高数书中用这么一段话描述方向导数: 偏导数反映的是函数沿坐标轴方向的变化率但许多物理现象告诉我们,只考虑函数沿坐标轴方向的变化率是不够的。例如,热空气要向冷的地方流动，气象学中就要确定大气温度、气压沿着某些方向的变化率因此我们有必要来讨论函数沿任一指定方向的变化率问题。

 

再来看方向导数的定义式:

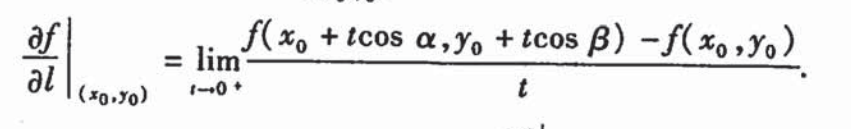
和偏导数不一样的是，方向导数对x变量和y变量都有了改变，而且有了角度，这个角度就体现了上述所说的沿任一指定方向。

 

 封面来自:【3d动画】偏导数的几何意义_哔哩哔哩_bilibili