题目一

试题编号： 202212-1
试题名称： 现值计算
时间限制： 1.0s
内存限制： 512.0MB
问题描述：
问题描述
评估一个长期项目的投资收益，资金的时间价值是一个必须要考虑到的因素。简单来说，假设银行的年利率为 5，那么当前的 100 元一年后就会变成 105 元，两年后变成 110.25 元。因此，现在收到 100 元比两年后收到 100 元收益更多，两年后再支出 100 元会比立刻支出 100 元更加划算。

基于上述分析，我们使用如下的模型来衡量时间价值：假设银行的年利率为 i，当前（第 0 年）的 x 元就等价于第 k 年的 x*(1+i)^k 元；相应的，第 k 年的 x 元的当前价值实际为 x*(1+i)**(−k) 元。

现给出某项目未来 n 年的预计收入支出情况，在将所有款项转换为当前价值后，试计算该项目的总收益。

输入格式
从标准输入读入数据。

输入的第一行包含空格分隔的一个正整数 n 和一个实数 i，分别表示年数和银行年利率。

输入的第二行包含空格分隔的 n+1 个整数，依次表示该项目第 0,1,⋯,n 年的预计收入（正数）或支出（负数）。

输出格式
输出到标准输出中。

输出一个实数，表示该项目在当前价值标准下的总盈利或亏损。

样例输入
2 0.05
-200 100 100

样例输出
-14.059

样例说明
该项目当前支出 200 元，在接下来两年每年收入 100 元。虽然表面看起来收支相抵，但计算当前价值可知总共亏损了约 14.059 元。

子任务
全部的测试数据满足 0<n≤50，0<i<1 且 i 的有效数字不多于 3 位，每年预计收入（正数）或支出（负数）的绝对值不大于 1000。

评分方式
如果你输出的浮点数与参考结果相比，满足绝对误差不大于 0.1，则该测试点满分，否则不得分。

提示
C/C++：建议使用 double 类型存储浮点数，并使用 scanf(“%lf”, &x); 进行输入，printf(“%f”, x); 进行输出。

Python：直接使用 print(x) 进行输出即可。

Java：建议使用 double 类型存储浮点数，可以使用 System.out.print(x); 进行输出。

题目分析（个人理解）

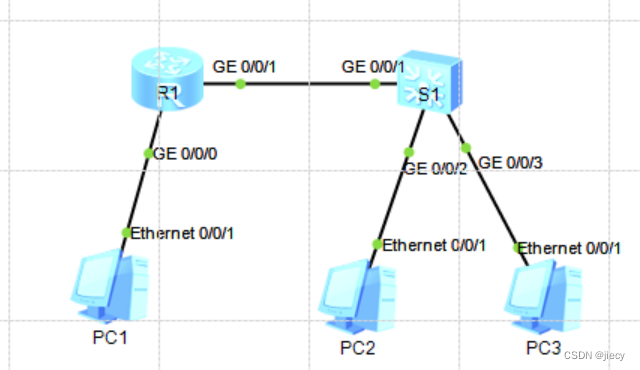
1. 先看输入，第一个是int类型，第二个是float类型，分别表示年数和银行年利率。
2. 第二行的参数输入的是每年的收入，我完全可以算出每一年收入的当前价值然后求和，如果是负数那就是亏了，如果是正数那就是盈利。具体的当前价值转换公式已经给出。
3. 直接上代码！！！

# 接收题目的第一行输入
a = input().split()
# 赋予接收的n的值
n = int(a[0])
# 赋予接收的i的值
i = float(a[1])
# 接收题目中第 0,1,⋯,n 年的预计收入（正数）或支出（负数）
money = [i for i in map(int, input().split())]
# 设置一个当前价值的总值，初始为0
all = 0
# 将每年的价值转化成当前价值，再加到总值中去
for j in range(n+1):
    all += money[j]*(1+i)**(-j)
# 最后输出总值
print("%.3f"%all)

题目二

试题编号： 202212-2
试题名称： 训练计划
时间限制： 1.0s
内存限制： 512.0MB
问题描述：
问题背景
西西艾弗岛荒野求生大赛还有 n 天开幕！

问题描述
为了在大赛中取得好成绩，顿顿准备在 n 天时间内完成“短跑”、“高中物理”以及“核裂变技术”等总共 m 项科目的加强训练。其中第 i 项（1≤i≤m）科目编号为 i，也可简称为科目 i。已知科目 i 耗时 ti 天，即如果从第 a 天开始训练科目 i，那么第 a+ti−1 天就是该项训练的最后一天。

大部分科目的训练可以同时进行，即顿顿在同一天内可以同时进行多项科目的训练，但部分科目之间也存在着依赖关系。如果科目 i 依赖科目 j，那么只能在后者训练结束后，科目 i 才能开始训练。具体来说，如果科目 j 从第 a 天训练到第 a+tj−1 天，那么科目 i 最早只能从第 a+tj 天开始训练。还好，顿顿需要训练的 m 项科目依赖关系并不复杂，每项科目最多只依赖一项别的科目，且满足依赖科目的编号小于自己。那些没有任何依赖的科目，则可以从第 1 天就开始训练。

对于每一项科目，试计算：

1）最早开始时间：该科目最早可以于哪一天开始训练？

2）最晚开始时间：在不耽误参赛的前提下（n 天内完成所有训练），该科目最晚可以从哪一天开始训练？

n 天内完成所有训练，即每一项科目训练的最后一天都要满足 ≤n。需要注意，顿顿如果不能在 n 天内完成全部 m 项科目的训练，就无法参加大赛。这种情况下也就不需要再计算“最晚开始时间”了。

输入格式
从标准输入读入数据。

输入共三行。

输入的第一行包含空格分隔的两个正整数 n 和 m，分别表示距离大赛开幕的天数和训练科目的数量。

输入的第二行包含空格分隔的 m 个整数，其中第 i 个（1≤i≤m）整数 pi 表示科目 i 依赖的科目编号，满足 0≤pi<i；pi=0 表示科目 i 无依赖。

输入的第三行包含空格分隔的 m 个正整数，其中第 i 个（1≤i≤m）数 ti 表示训练科目 i 所需天数，满足 1≤ti≤n。

输出格式
输出到标准输出中。

输出共一行或两行。

输出的第一行包含空格分隔的 m 个正整数，依次表示每项科目的最早开始时间。

如果顿顿可以在 n 天内完成全部 m 项科目的训练，则继续输出第二行，否则输出到此为止。

输出的第二行包含空格分隔的 m 个正整数，依次表示每项科目的最晚开始时间。

样例 1 输入
10 5
0 0 0 0 0
1 2 3 2 10

样例 1 输出
1 1 1 1 1
10 9 8 9 1

样例 1 说明
五项科目间没有依赖关系，都可以从第 1 天就开始训练。

10 天时间恰好可以完成所有科目的训练。其中科目 1 耗时仅 1 天，所以最晚可以拖延到第 10 天再开始训练；而科目 5 耗时 10 天，必须从第 1 天就开始训练。

样例 2 输入
10 7
0 1 0 3 2 3 0
2 1 6 3 10 4 3

样例 2 输出
1 3 1 7 4 7 1

样例 2 说明
七项科目间的依赖关系如图所示，其中仅科目 5 无法在 10 天内完成训练。

具体来说，科目 5 依赖科目 2、科目 2 又依赖于科目 1，因此科目 5 最早可以从第 4 天开始训练。

样例 3 输入
10 5
0 1 2 3 4
10 10 10 10 10

样例 3 输出
1 11 21 31 41

子任务
70 的测试数据满足：顿顿无法在 n 天内完成全部 m 项科目的训练，此时仅需输出一行“最早开始时间”；

全部的测试数据满足 0<n≤365 且 0<m≤100。

题目分析（个人理解）

1. 注意此题目的依赖关系，只存在编号在后面的依赖编号在前面的科目，看完题目首先想到的是递归思想。
2. 大概思路是先求每个科目最早开始时间，然后判断是否在最早开始的情况下能否完成课程任务，如果不能那就只输出最早开始时间，如果能，那就进入寻找最晚开始时间的判断。
3. 如何求最早开始时间？
4. 可以遍历每一个科目判断是否被依赖，如果不用依赖其他科目，那很简单最早开始时间就是1，如果需要依赖其他，那就加上需要依赖的课程的持续时间，就是当前课程开始的最早时间。然后判断每一个课程的最早开始时间加上持续时间如果大于截止时间那就说明完成不了全部课程，也就不需要进行下一步（最晚时间的判断）。其实本题可以理解给定一个时间轴，那么最早时间的判断实际是优先数轴最左边安排课程，如果是找最晚开始时间就是优先时间轴右边安排。
5. 对于输出可以将最早时间和最晚时间分别存在两个列表中，最后只需要遍历列表输出即可。使用mark作为一个开关，如果值为1就说明在每科最早开始的情况下完成了所有课程，为0则表示没有完成。
6. 现在如何判断在完成每一个课程的条件下，每一科最晚开始时间，那么可以从后往前遍历，判断哪些课程被依赖，如果有被依赖，那么最晚开始时间 = 依赖它的科目的最晚开始的时间-本身的持续时间的时刻，如果被依赖的后面还存在依赖关系（假如事件从a到c，b依赖a，c依赖b，b作为第一个遍历的对象，先将b放入时间轴的最右边，被依赖的b给不被依赖的事件c让位，让的就是不被依赖的事件的持续时间），那么用递推的思想去理解就OK。
7. 如果不是被依赖的科目，那么最晚开始时间 = 最后期限 - 持续时间的时刻。
8. 上代码！！！

n, m = map(int, input().split())
p = [0] + [i for i in map(int, input().split())]
t = [0] + [i for i in map(int, input().split())]
earliest = [0 for _ in range(m + 1)]
latest = [0 for _ in range(m + 1)]
mark = 1
# 将每个科目的最早时间确定
for i in range(1, m + 1):
    if p[i] == 0:
        earliest[i] = 1
    else:
        earliest[i] = earliest[p[i]] + t[p[i]]
    # 判断所有科目最早开始的情况是否可以完成所有科目
    if earliest[i] + t[i] - 1 > n:
        mark = 0
# 输出每项科目的最早开始时间
print(*earliest[1:])

# 判断是否可以完成项目
if mark == 1:
    # 将确定每个科目的最晚，从最后的科目往前推，需要把依赖该科目的科目所消耗时间算上
    for i in range(m, 0, -1):#从最底层开始遍历
        temp = 366#存最晚开始时间
        for j in range(i + 1, m + 1):
            # 寻找是否有依赖该科目的科目
            if p[j] == i:
                temp = min(temp, latest[j])#找最晚开始时间，用min是如果存在多层依赖关系取更高一层的值
           
        # 如果没有被依赖，那么最晚开始时间 = 最后期限 - 持续时间的时刻
        if temp == 366:
            latest[i] = n - t[i] + 1
        # 如果有被依赖，那么最晚开始时间 = 依赖它的科目的最晚开始的时刻最小的科目 - 本身的持续时间的时刻
        else:
            latest[i] = temp - t[i]#被依赖的给不被依赖的事件让位，让的就是不被依赖的事件的持续时间
    # 输出每项科目的最早开始时间
    print(*latest[1:])

总结