文章目录
- 参考
- 环境
- 声明
- 八位二进制加法器
- 八进制数值
- 原码
- 概念
- 正负数与零
- 正数与负数的运算
- 反码
- 概念
- 一步之遥
- 补码
- 概念
- 唯一的零
- 加法运算
- 补码的优缺点
- 优点
- 简化算术运算
- 一眼辨别正负性
- 运算过程中无需对符号位进行处理
- 缺点
- 不易阅读
参考
| 项目 | 描述 |
|---|---|
| 搜索引擎 | Bing、Google |
| AI 大模型 | 文心一言、通义千问、讯飞星火认知大模型、ChatGPT |
| 哔哩哔哩 | 看得视频太多😭 |
环境
| 项目 | 描述 |
|---|---|
| PHP | 5.5.0、5.6.8、7.0.0、7.2.5、7.4.9、8.0.0、8.2.9 |
| PHP 编辑器 | PhpStorm 2023.1.1(专业版) |
| 绘图工具 | draw.io 21.7.5 |
声明

八位二进制加法器
八位二进制加法器是一种 电子电路,用于 执行两个八位二进制数的加法操作。这种加法器可以将两个八位的二进制数相加,得出一个八位的二进制和。对此,请参考如下示例:
A: 1 0 1 1 0 1 0 1
B: 0 1 1 0 1 0 1 1
-----------------------
Sum: 1 1 0 1 1 1 0 0
在这个示例中,每一位的相加操作都遵循标准的二进制加法规则,包括 进位。如果两个位相加后的和大于 1,那么就会产生进位,这个进位会被加到下一位的操作中。如果进位将被应用在第九位二进制位中,则该进位将被抛弃。
八进制数值
在本篇文章中,我们都将 模拟八位二进制加法器进行加法操作。故将整数表示为八位二进制数,这并 不意味着 采用原码、反码及补码 仅能够 用于将整数转化为 八位 二进制数。
原码
概念
原码是一种整数的二进制表示方法,也被称为 符号-数值表示法。原码主要用于表示 有符号整数(正数、负数和零),在计算机系统中广泛使用。
在二进制数的原码表示中,二进制数被分为了 两部分,即 符号位 与 数值具体数值。
- 符号位
原码的最高位是符号位。符号位用来表示数值的正负性,0表示正数,1表示负数。 - 具体数值
符号位之后的二进制数字均用于表示具体数值。
举个栗子
数值 2 采用七位二进制数表示为 0000010。若需要表示数值的 正负性,则 在二进制数的最高位前 添加一个二进制位。若该二进制位存放数字 1,则该二进制数值表示十进制数 -2;若该二进制位存放数字 0,则该二进制数值表示十进制数 2。
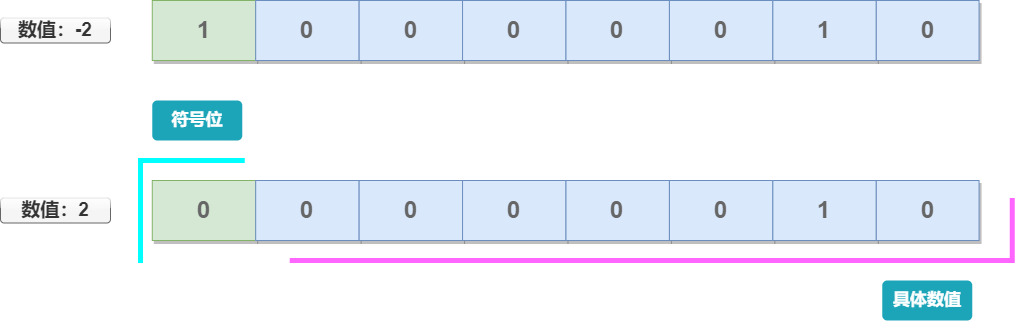
正负数与零
零既不是正数,也不是负数。使用原码表示数值存在缺陷,即 零有了正负性,存在正零与负零。
在原码表示法中,由于我们直接使用 二进制数的最高位作为符号位,因此当其他所有二进制位都为 0 时,我们会得到数值零的两种不同表示,即 正零 与 负零。这显然是不合理的。表示零的 冗余性 是原码的主要缺陷之一,也是计算机 不使用原码存储整数的原因之一。

正数与负数的运算
原码能够表示正负数,但在进行正数与负数的加法运算时会出现问题。对此,请参考如下示例:
已知 +2 的二进制表示为 00000010,而 -2 的二进制表示为 10000010。两者进行加法,
00000010
10000010
---------
10000100
得到的结果为 10000100,转化为十进制数为 -4。 +2 与 -2 相加,结果应为零,但却得到了 -4。原码能够表示正数、负数与零,但 无法正确处理正数与负数的加法运算,这是计算机 不使用原码存储整数的另一原因。
反码
概念
反码同原码一般,均用于 有符号十进制整数的二进制表示。反码基于原码 得来,对于正数与负数,得到反码的方式存在如下不同:
- 正数的反码即其原码。
- 负数的反码是其原码中除符号位外的二进制位
按位取反(每一个二进制数,由 0 变 1 或 由 1 变 0)得来。
举个栗子
+5 的反码表示为:00000101
-5 的原码表示为:10000101
-5 的反码表示为:11111010
一步之遥
反码与原码具有相同的缺陷,均存在两种表示零的方式,即正零与负零。+0 的反码表示为 00000000,-0 表示为 11111111。

反码可以实现 正数与负数 或 负数与负数之间的加法运算。对此,请参考如下示例:
举个栗子
+3 的反码表示为:00000011
-5 的反码表示为:11111010
两者相加:
00000011
11111010
---------
11111101
得到的 11111101 是结果的反码表示,我们需要将其进行 逆反码运算。尝试将除符号位外的二进制位按位取反,可得 10000010,转化为十进制数值,结果为 -2。
补码
概念
在计算机中,整数的存储通常采用其补码表示。补码同反码与原码一般,均用于 有符号十进制整数的二进制表示。补码基于反码 得来,对于正数与负数,得到补码的方式存在如下不同:
- 正数的补码、原码与反码均相同。
- 负数的补码为其
反码 + 1。
唯一的零
在有符号的十进制整数的补码表示中,零的表示方式只有一种,即 00000000。
通过对负数的反码进行 +1 的操作,-0 的反码表示由 11111111 变为了 100000000,第九位二进制数 1 由于没有地方安放,故被抛弃。于是 0 只存在 00000000 这一种表示。
加法运算
在进行 补码之间的加法运算 后,得到的结果需要进行 逆补码运算 以求得人类容易理解的二进制表示,方便将结果转化为 十进制数值。对此,请参考如下示例:
+3 的补码表示为:00000011
-5 的补码表示为:11111011
两者相加:
00000011
11111011
---------
11111110
得到的 11111110 是结果的补码表示。为方便将其转化为正确的十进制数,我们需要 对其进行逆补码运算以求得其原码表示。首先对 11111110 进行 -1 处理得到 11111101,再 对除符号位外的二进制位进行按位取反运算 得到 10000010,转化为十进制数得到最终结果 -2。
补码的优缺点

优点
简化算术运算
通过将整数转化为二进制的补码表示,加法和减法运算便可以 使用相同的硬件电路进行处理。当进行 两个正整数的减法运算 时,只需要 将减数理解为负数 再与被减数进行加法运算即可。对此,请参考如下示例:
10 - 5 = ?
上述表达式可以理解为:
10 + (-5) = ?
只需将减数 5 理解为 (-5) 便可将减法运算转化为加法运算。
使用 相同的硬件电路进行加法与减法的处理 能够带来如下优点:
- 硬件简化
当加法和减法使用相同的电路时,可以减少计算机中所需的硬件组件数量,这降低了系统的成本和复杂度。

- 节省空间
由于只需要一个通用的加法电路,计算机的物理尺寸可以更小。这对于嵌入式系统和移动设备非常重要,因为它们通常具有有限的空间。 - 降低功耗
使用相同的硬件电路执行加法和减法操作可以降低功耗。这对于移动设备等电池供电的系统来说尤为重要,因为降低功耗可以延长电池寿命并提高设备的续航能力。 - 提高性能
使用相同的硬件电路可以提高计算机的性能,因为该电路可以被高度优化和并行化,以加快算术运算速度。
一眼辨别正负性
由于补码的 最高位为符号位,表示着数值的正负性。故只需要观察补码的最高位存放的是二进制数 1 还是 0,便可确定该数值的 正负性。
运算过程中无需对符号位进行处理
在进行不同或相同(正负性)符号 的补码运算时,无需对符号位进行特殊处理,符号位与补码中的其他二进制位可一同进行加法或减法运算。
缺点
不易阅读
在进行加或减的补码运算后,得到的结果是其补码表示。若需要自行将其转化为十进制数,往往需要先通过 逆补码运算,即 进行补码到原码的还原过程。在得到原码后便可 轻松的 将其转化为十进制数。