最近CV领域各种大模型在图像生成领域大发异彩,比如这两年大火的dalle系列模型。在这些模型中用到一个基础模型vqvae,今天我们写个简单实现来了解一下vqvae的工作原理。vqvae原始论文连接https://arxiv.org/pdf/1711.00937.pdf
1,代码
首先我们直接来看代码实现,完整代码GitHub - Pillars-Creation/vqvae: 使用vqvae 进行用户和物品冷启动
def vector_quantizer(self, z):
# 将 z 的形状更改为 [batch_size, embedding_dim, 1]
z_flat = z.view(-1, self.codebook_dim, 1)
# 计算 z_flat 两两相乘的结果
z_flat = torch.matmul(z_flat, z_flat.transpose(1, 2))
z_flat = torch.sqrt(z_flat)
# 计算z_flat中每个潜在向量与码本中所有向量之间的欧几里得距离
distances = torch.cdist(z_flat, self.codebook)
# 计算与每个潜在向量z最接近的码本向量的索引
codebook_indices = torch.argmin(distances, dim=-1)
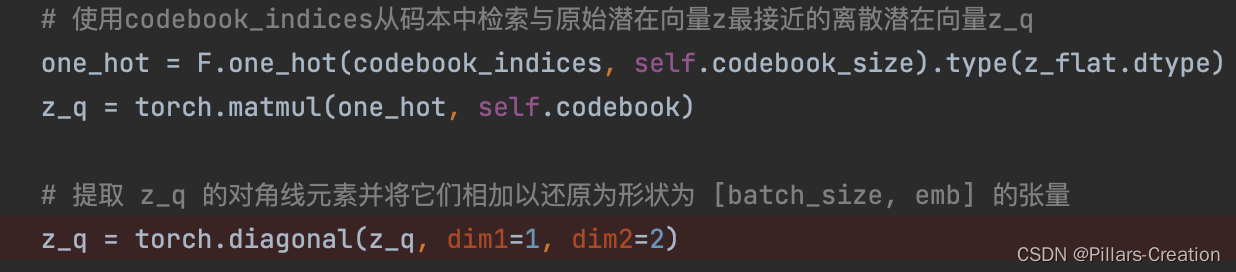
# 使用codebook_indices从码本中检索与原始潜在向量z最接近的离散潜在向量z_q
one_hot = F.one_hot(codebook_indices, self.codebook_size).type(z_flat.dtype)
z_q = torch.matmul(one_hot, self.codebook)
# 提取 z_q 的对角线元素并将它们相加以还原为形状为 [batch_size, emb] 的张量
z_q = torch.diagonal(z_q, dim1=1, dim2=2)
# 计算VQ损失,vq_loss为标量
vq_loss = torch.mean(torch.square(z_q.detach() - z))
commit_loss = torch.mean(torch.square(z.detach() - z_q))
vq_loss += self.commitment_cost * commit_loss
# Apply the Straight-Through Estimator (STE) trick
z_q = z + (z_q - z).detach()
# 计算困惑度
avg_probs = torch.mean(one_hot, dim=0)
perplexity = torch.exp(-torch.sum(avg_probs * torch.log(avg_probs + 1e-10)))
# VQ-VAE Decoder
z_q = z_q.view(z.shape)
return z_q, vq_loss, perplexity2,为什么是vqvae,
要回答这个问题,我们看看vqvae论文里作者认为和传统vae模型的关键差异点。从论文可以看到作者认为关键差异点有两个一个是使用了离散编码,一个是动态的学习先验分布

离散编码
- VAE通过在编码器中引入隐变量(通常是高斯分布的样本)来建模数据的潜在分布。这种连续性的隐空间使得VAE在生成新样本时更加灵活。通过在隐空间中进行插值或随机采样,可以生成具有连续变化的新样本。但是VAE模型存在一个问题是后验奔溃
- 后验奔溃是指在训练过程中,编码器学到的潜在表示几乎没有包含输入数据的任何有用信息,而解码器主要依赖于其自身来生成数据。这种情况下,VAE 的生成性能会受到影响,因为潜在空间没有学到有效的数据表示。
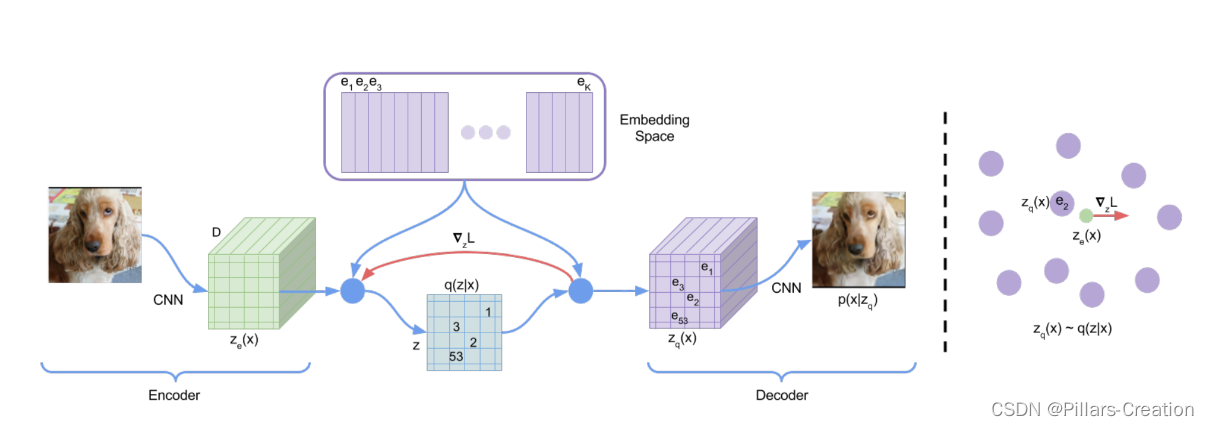
- 在VQ-VAE中,编码器将输入数据映射到一个离散的隐藏,将编码器的输出与一个称为码本(codebook)的离散向量集进行匹配来实现的。使用一个离散编码表来表达连续分布。这种离散的隐藏表示具有一些优势,例如更高的表示能力和更好的泛化性能。
动态的学习先验分布
这块比较直观,在传统的 VAE 中,先验分布通常是一个固定的分布,例如标准正态分布。这意味着潜在变量应该遵循这个固定的分布,这是一个静态的约束。然而,在 VQ-VAE 中,先验分布是从数据中学习的,这意味着它可以根据数据的特点自适应地改变。这个学习的先验分布是通过优化码本中的离散向量来实现的。
在训练过程中,码本中的向量会根据输入数据和重构误差进行更新,从而学习到一个更适合表示数据的离散潜在空间。因此,当我们说 VQ-VAE 中的先验是学习的而不是静态的,潜在空间(即码本)可以根据数据自适应地调整。
3,代码里几个注意点
1,Straight-Through Estimator (STE) trick
vqvae因为要和codebook 取argmin,由于argmin不可导。所以要用STE技术。
STE是一种用于训练离散变量(例如二值变量)的神经网络的技巧。源于Benjio的论文《Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation》
Straight-Through的思想分两个部分,
前向传播的时候可以用想要的变量(哪怕不可导),
而反向传播的时候,用你自己为它所设计的梯度。
根据这个思想,我们设计的目标函数是:
其中detach()是stop gradient的意思。这样一来,前向传播计算(求loss)的时候,就直接等价于decoder(z+zq−z)=decoder(zq),然后反向传播(求梯度)的时候,由于zq−z不提供梯度,所以它也等价于decoder(z),这个就允许我们对encoder进行优化了。
2,codebook
在cv里码本对应的encoder是卷积完的三维机构,如果我们是优化ID向量只有一维,需要做个转换把一维变成二维,这里可以用卷积,也可以把向量两两相乘变成二维结构,这样的好处是一方面方便我们把每一行当作一个向量和codebook求对应,另一方面两两相乘也可以理解为一种特征交叉,提升了向量的表达。如代码中实现
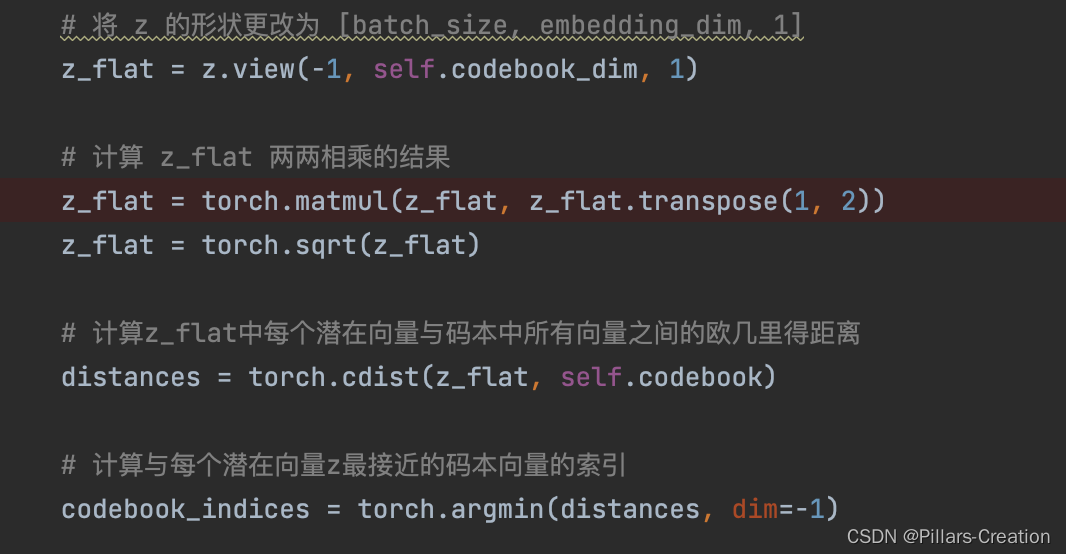
3,提取对角线元素,
因为刚刚encode的时候我们做了两两相乘生成了个二维矩阵,所以从codebook中取得映射后,也是个二维矩阵,我们对应的取对角线值,把向量还原为一维,对应代码
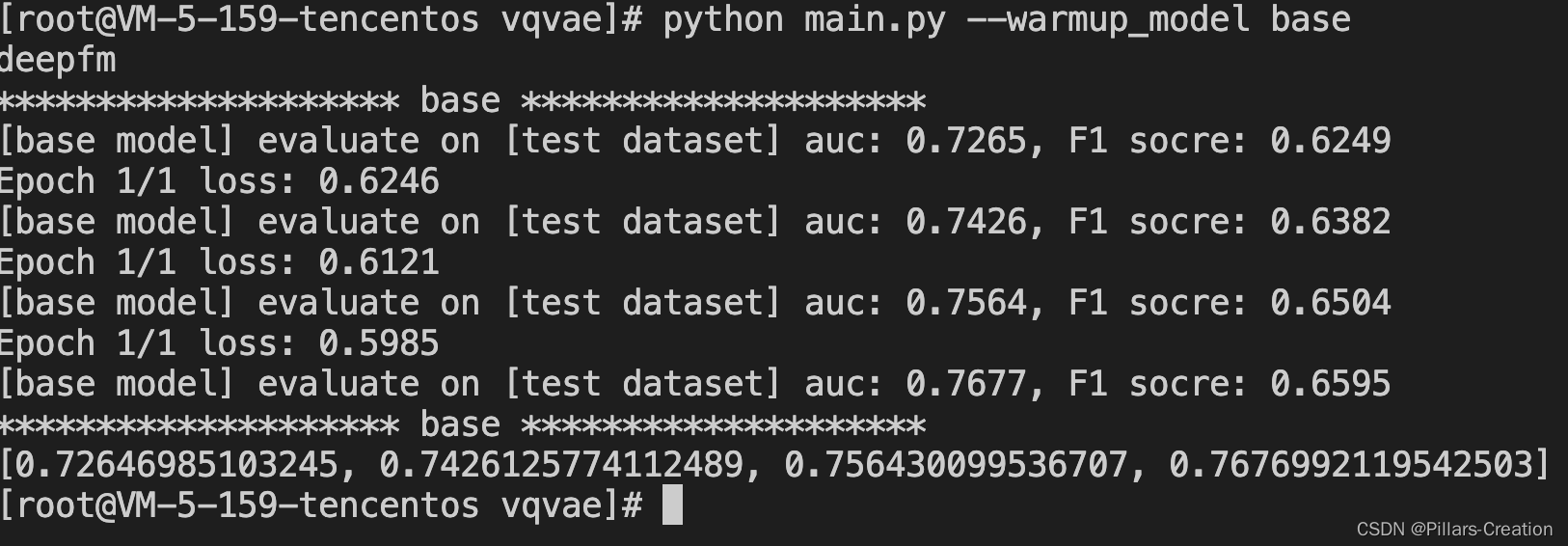
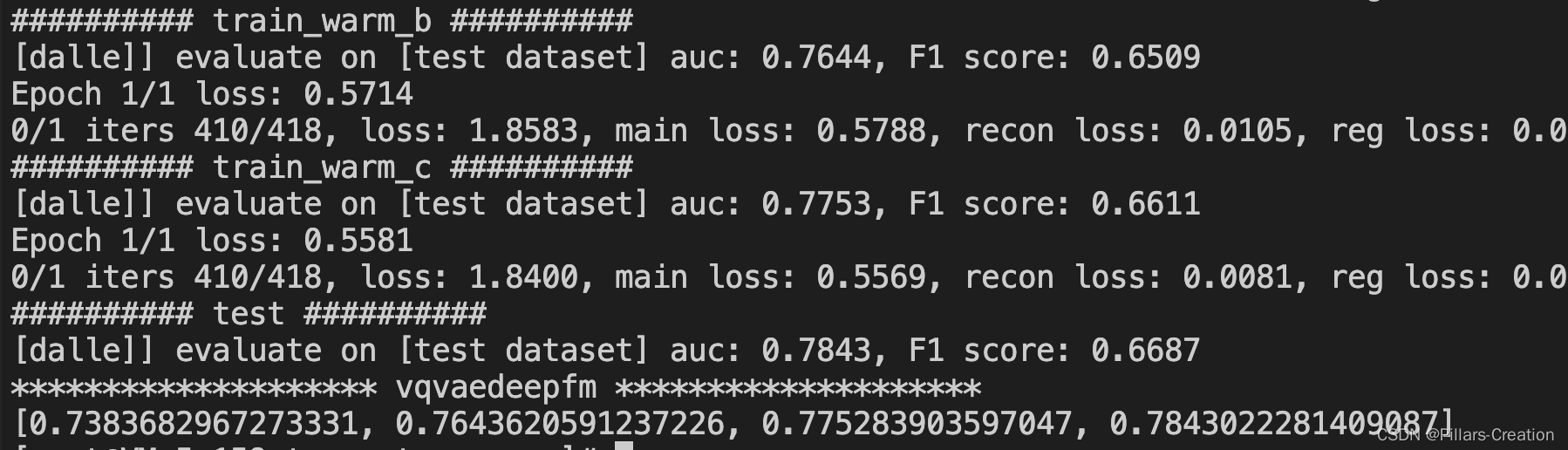
4.实验效果
在movilen的数据集上对物品ID做了增强,可以看到效果还是不错的



![[初始java]——java为什么这么火,java如何实现跨平台、什么是JDK/JRE/JVM](https://img-blog.csdnimg.cn/e4da53910be24eaca3508d32a22f8c69.png)




![论文笔记[156]PARAFAC. tutorial and applications](https://img-blog.csdnimg.cn/62c9ad9a573741e78993eb571431a58f.png)