【数据结构与算法】堆排序(向下和向上调整)、TOP-K问题（超详细解读）

前言：

💥🎈个人主页:Dream_Chaser～ 🎈💥

✨✨专栏:http://t.csdn.cn/oXkBa

⛳⛳本篇内容:c语言数据结构--堆排序，TOP-K问题

堆排序

1.二叉树的顺序结构

1.1父节点和子节点的关系

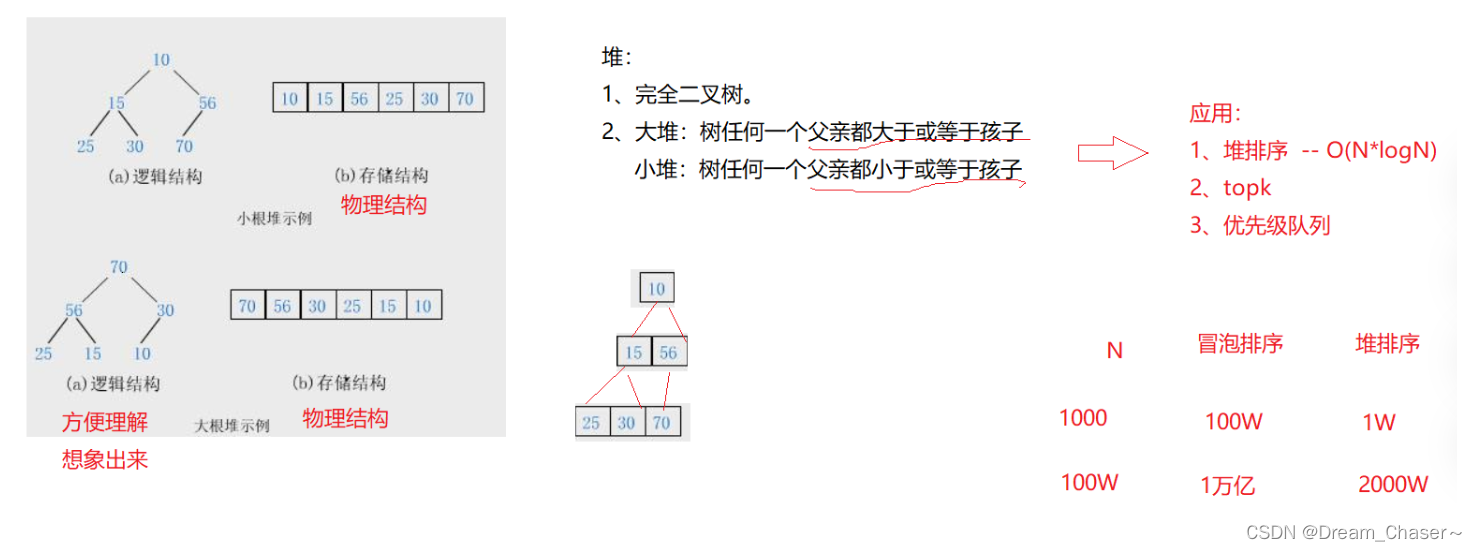
2 堆的概念及结构

3. 堆的实现

3.1堆的自定义类型

3.2堆的向上调整算法

3.3堆的向下调整算法

3.4堆的初始化

3.5堆的插入

3.6堆的删除

3.7获取堆顶元素

3.8堆的判空

3.9返回堆中有效个数

3.10堆的销毁

4.堆的应用

4.1堆排序

4.1.1堆排序的本质

4.1.2向上调整建堆

向上调整算法建堆的时间复杂度:O(N):F(N)= (N+1)*(log(N+1)-2)+ 2

特别注意:向下调整(父节点下标是0)

4.1.3向下调整建堆(动图)

向下调整算法建堆的时间复杂度: O(N)=N - log(N+1)

4.2TOP-K问题

4.2.1生成随机数并写入文件

4.2.2建立小堆并比较元素进行合理替换

5.总代码

test.c

Heap.h

Heap.c

堆排序

1.二叉树的顺序结构

顺序存储

顺序结构存储 就是使用 数组来存储 ，一般使用 数组只适合表示完全二叉树 ，因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储，关于堆我们后面的章节会专门讲解。 二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。

普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而 完全二叉树更适合使用顺序结构存储 。现实中我们通常把 堆(一种二叉树) 使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统 虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段

1.1父节点和子节点的关系

经过观察，可得知父子间下标关系::

父亲下标找孩子:

leftchild = parent*2+1

rightchild = parent*2+2

孩子下标找父亲:

parent = (child-1) / 2

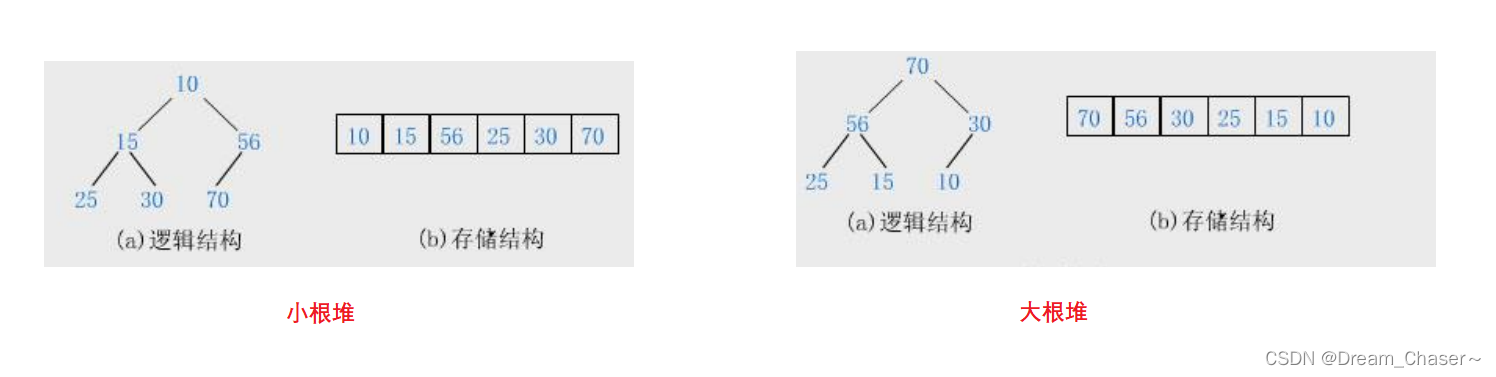
2 堆的概念及结构

堆 : 如果有一个关键码的集合K = {k0,k1,k2,…,kn-1}, 把它的所有元素按 完全二叉树 的 顺序存储 方式存储在一个一维数组中，并满足ki<=k2i+1且ki<=k2i+2（或满足ki>=k2i+1且ki>=k2i+2），其中i=0,1,2,…，则称该集合为堆。

大堆：将根节点最大的堆叫做最大堆或大根堆，

小堆：将根节点最小的堆叫做最小堆或小根堆。

堆的性质：

堆中某个节点的值总是不大于或不小于其父节点的值；

堆总是一棵完全二叉树。

堆的结构:

选择题

1. 下列关键字序列为堆的是：（）

A 100 , 60 , 70 , 50 , 32 , 65

B 60 , 70 , 65 , 50 , 32 , 100

C 65 , 100 , 70 , 32 , 50 , 60

D 70 , 65 , 100 , 32 , 50 , 60

E 32 , 50 , 100 , 70 , 65 , 60

F 50 , 100 , 70 , 65 , 60 , 32

答案：A

解析：只有A满足大堆的条件

100

60 70

50 32 65

而其它选项均不满足大堆或小堆的情况。

3. 堆的实现

3.1堆的自定义类型

头文件的引用

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

结构体类型的定义

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;//数组
	int size;//有效数据个数
	int capacity;//容量
}HP;

3.2堆的向上调整算法

假设一个数组，前提条件是它已经是一个堆了，这时候需要在数组后插入一个元素，要保证此数组仍是一个堆的结构，那么这时候就需要用到向上调整的算法。

关于此题，向上调整算法的思想是:

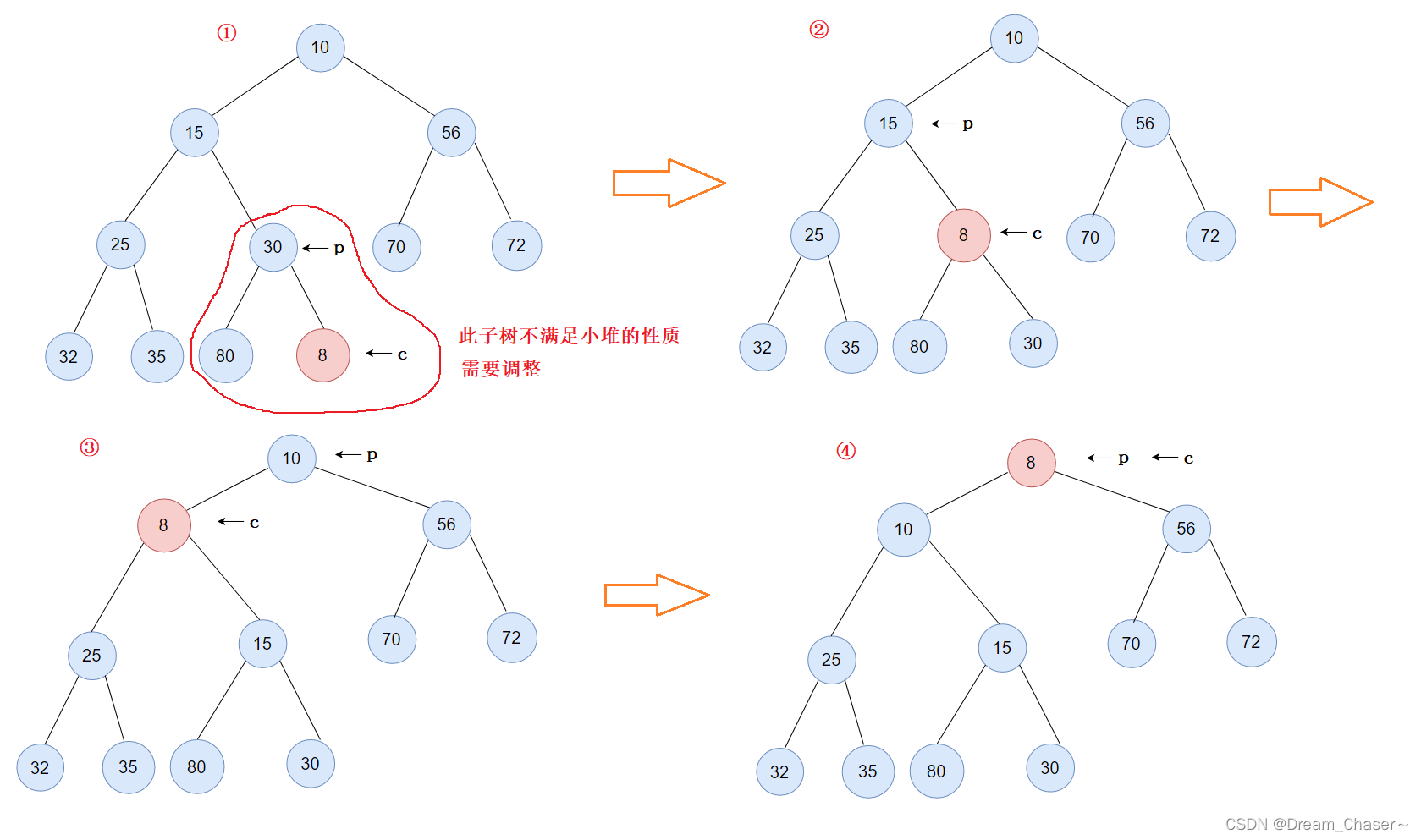
①已经建好一个小根堆的前提下，插入一个元素8,要保证此刻的堆仍是一个小堆，那就需要求出节点8的父亲节点的下标，比较此时节点8与其父节点的大小，判断是否需要交换位置。

②若目标节点值的大小比其父节点小，那么需要交换目标节点的下标与其父节点的下标。并且将此刻的父节点作为新的目标节点，与其父节点比较，若值依旧比其要小，那就继续交换下标，一直到child下标的值为0结束交换过程。若一开始，目标节点大于其父节点的值，那么证明此刻的堆已经为小堆了，立刻跳出循环停止交换。

void Swap1(HPDataType* n1, HPDataType* n2)//交换函数
{
	HPDataType tmp = *n1;
	*n1 = *n2;
	*n2 = tmp;
}
堆的向上调整(未插入元素8前已是小堆)
void AdjustUp(int* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] < a[parent])//小堆
		{
			Swap1(&a[child], &a[parent]);

			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

3.3堆的向下调整算法

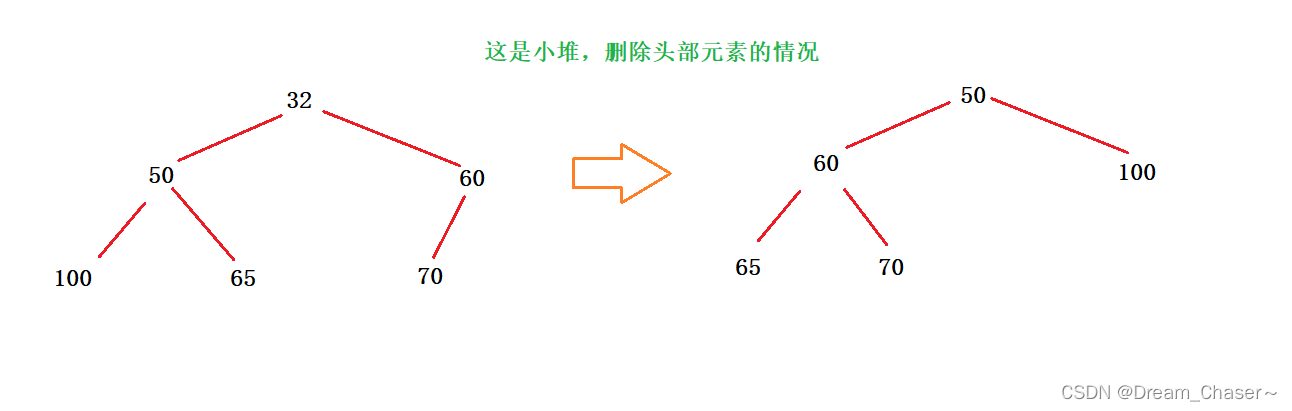
假设我们要删除一组数据里面的元素，未删除之前这组数据满足小堆/大堆的情况，那么该如何删除呢？

方法一:挪动覆盖删除堆顶元素，重新建堆

可以看到，挪动覆盖，不能保证数组还是堆，父子关系全变了,只能重新建堆，代价极大。那么试下另辟蹊径。

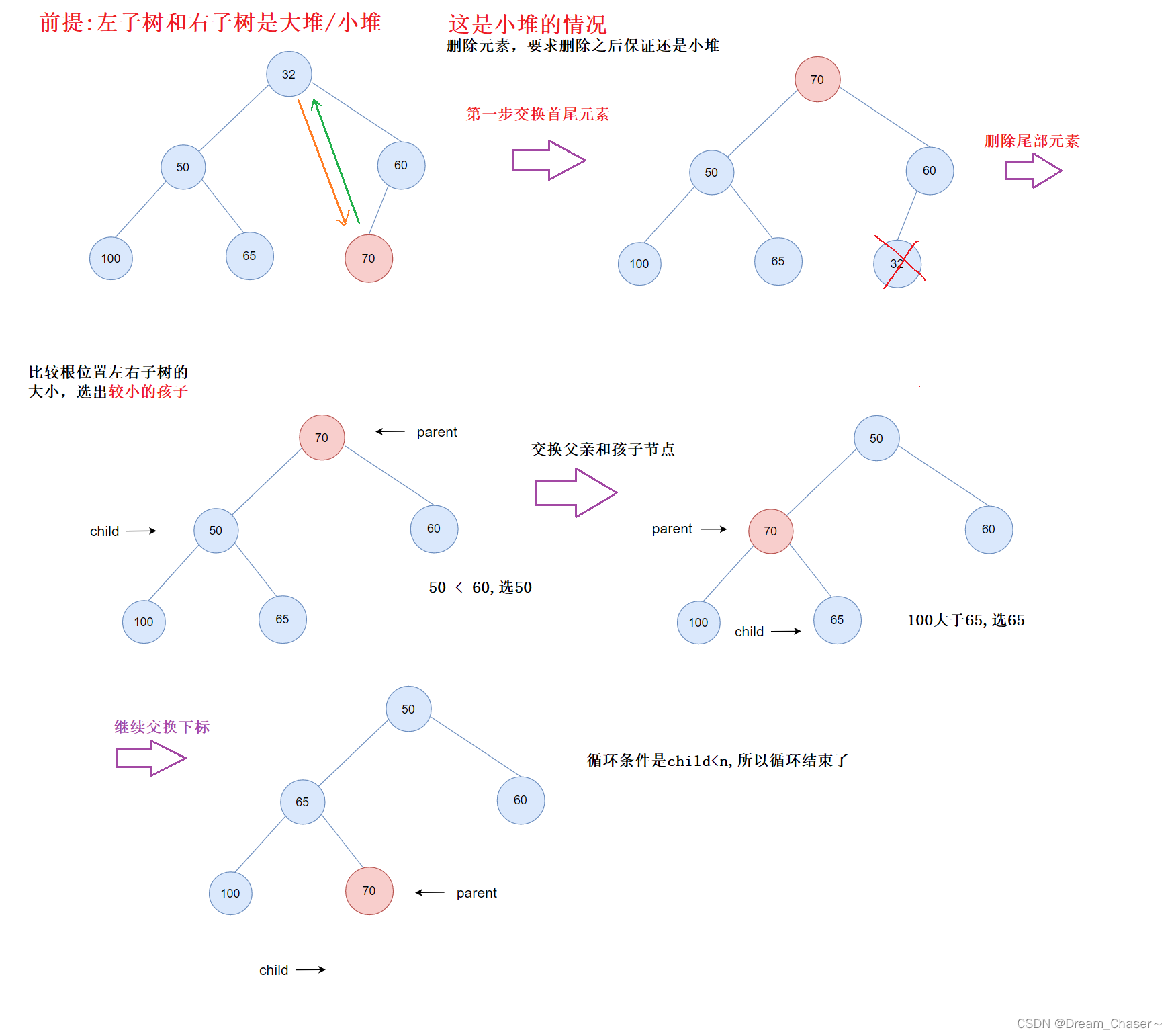
方法二：首尾数据交换，再删除，再调堆

此题前提条件为,给出一个小堆,要求删除一个元素之后，保证它还是一个小堆。

先说明一下向下调整的基本思想:

①先交换此时根节点的值与尾节点的值，接着删除尾节点的值，然后从交换后的根节点开始，选出左右子树中较小的孩子。

②让较小的孩子与根节点比较。

若此时的根节点(第一个父节点)的值大于较小的孩子节点，就让较小孩子的位置与根节点的位置互换，就像下图的70。并将较小孩子节点(第二个父节点)的位置作为新的父节点的下标，接着根据此父节点的值比较左右较小孩子的值，满足条件继续向下调整。

若此此时的根节点(第一个父节点)的值小于较小孩子节点的值，则证明此数组已为小堆，不需要调整，此刻跳出while循环。

代码实现:

void Swap2(HPDataType* x1, HPDataType* x2)
{
	HPDataType tmp = *x1;
	*x1 = *x2;
	*x2 = tmp;
}
void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{		//先判断是否越界的情况下，再判断两个孩子的大小；
		if (child + 1 < n && a[child] > a[child + 1])//假设左孩子小
		{
			child++;
		}

		if (a[child] < a[parent])
		{
			Swap2(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

3.4堆的初始化

初始化一个数组，用于存放堆中的元素；capacity表示堆的容量，size表示堆的有效个数。

void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->capacity = php->size = 0;
}

3.5堆的插入

将元素插入到数组中，并使有效个数size++，用于记录堆中元素的有效个数。并且，当插入第一个数的时候,就可以看作是堆。插入第二个元素的时候，假设要建的是小堆，那么就需要与跟节点比较大小，假设根节点大于子节点，那么就需要交换子节点与根节点的位置;若根节点小于子节点，那么就已是小堆不需要变位置。

这个插入函数需要运用到向上调整算法来帮助建堆，传入的是满二叉树的最后一层的最后一个结点，使其插入数据的时候仍然保持堆的性质。

void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{	//如果空间不够则扩容
		int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, newCapacity * sizeof(HPDataType));
		if (tmp == NULL)
		{
			perror("malloc fail\n");
			return;
		}
		php->a = tmp;
		php->capacity = newCapacity;
	}

	php->a[php->size] = x;
	php->size++;
    //向上调整
	AdjustUp(php->a, php->size - 1);
}

3.6堆的删除

堆的删除的是堆顶的数据，但如果用覆盖的方式来删掉，那么就会使得父子关系全乱了，还有可能原来的堆直接不是堆了，需要全部元素重新调整顺序建堆，时间复杂度是O(N)。

那么如果先将堆顶的数据与堆的最后一个节点的数据交换，之后再删除最后一个节点的数据，再通过一次在根节点处的向下调整，那么这时候就可以保持是堆的性质，并且时间复杂度变为O(log(N))

void Swap(HPDataType* a1, HPDataType* a2)
{
	HPDataType tmp = *a1;
	*a1 = *a2;
	*a2 = tmp;
}
void HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));

	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;

	AdjustDown(php->a, php->size, 0);
}

3.7获取堆顶元素

获取堆顶元素，下标对应着数组第一个元素。

HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));

	return php->a[0];
}

3.8堆的判空

判断堆是否为空，空返回true，非空返回false

bool HeapEmpty(HP* php)
{
	assert(php);

	return php->size == 0;
}

3.9返回堆中有效个数

获取堆的数据个数，即返回堆结构体中的size变量

int HeapSize(HP* php)
{
	assert(php);

	return php->size;
}

3.10堆的销毁

由于数组的空间是malloc出来的，那么需要free掉数组a的空间。再将a指针置空，并把堆的容量和有效个数的变量赋值成0

void HeapDestroy(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}

4.堆的应用

4.1堆排序

这里前提说一下：当我们用向上调整或者向下调整算法建成一个小堆或者大堆时，这时候的小堆和大堆，不一定是有序的，因为堆跟有序之间还存在明显的界限。

以小堆为例子：

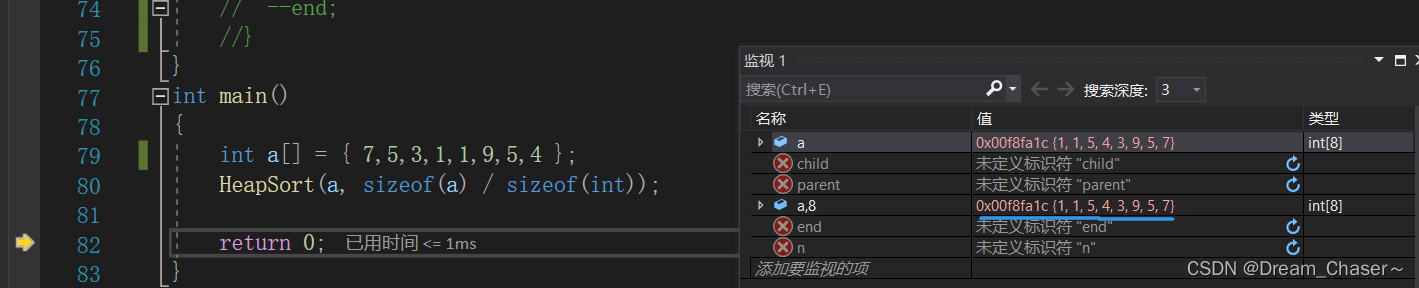
就比如说，要将 7,5,3,1,1,9,5,4 ，变成小堆的结果是: 1,1,5,4,3,9,5,7 , 并不是有序的

那么堆排序，说到底还是一个排序，那么排序肯定是要将数据排成升序 / 降序，那么建小堆，要排成升序还是降序呢？

先来看排成升序的情况：1,1,5,4,3,9,5,7 -> 1,1,3,4,5,5,7,9

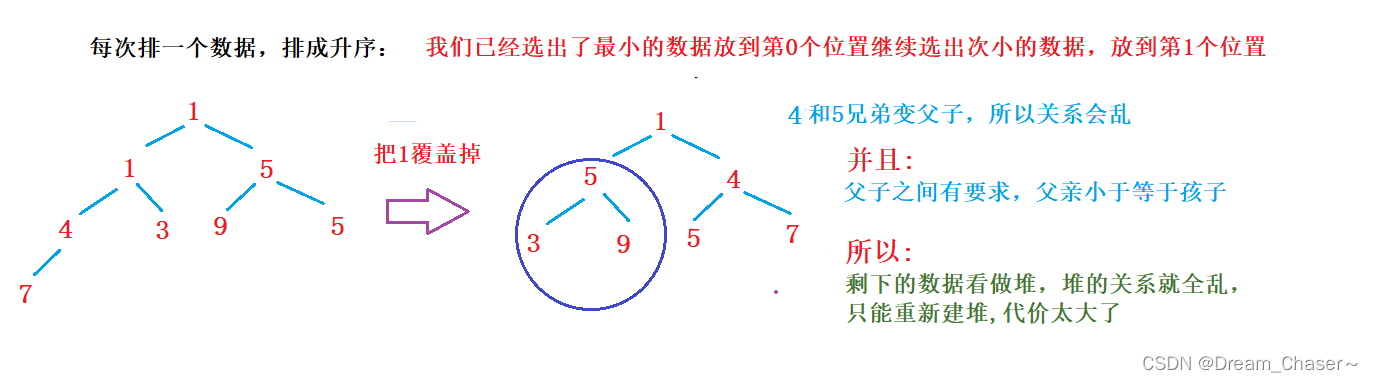所以小堆是要排成降序的

4.1.1堆排序的本质

堆排序正确思路是:

①先用向上调整或者向下调整，弄出一个小堆或者大堆。

②假定前面弄的是小堆，那么进入while循环，通过向下调整，那么这时候的小堆就会逐渐排成倒序。

如果这时候为大堆，通过向下调整，就会排成升序。

③依据题目的意图，可以轻易地选出最大或者最小的元素。

4.1.2向上调整建堆

那这时候我们就来看一下，先通过一次向上调整,

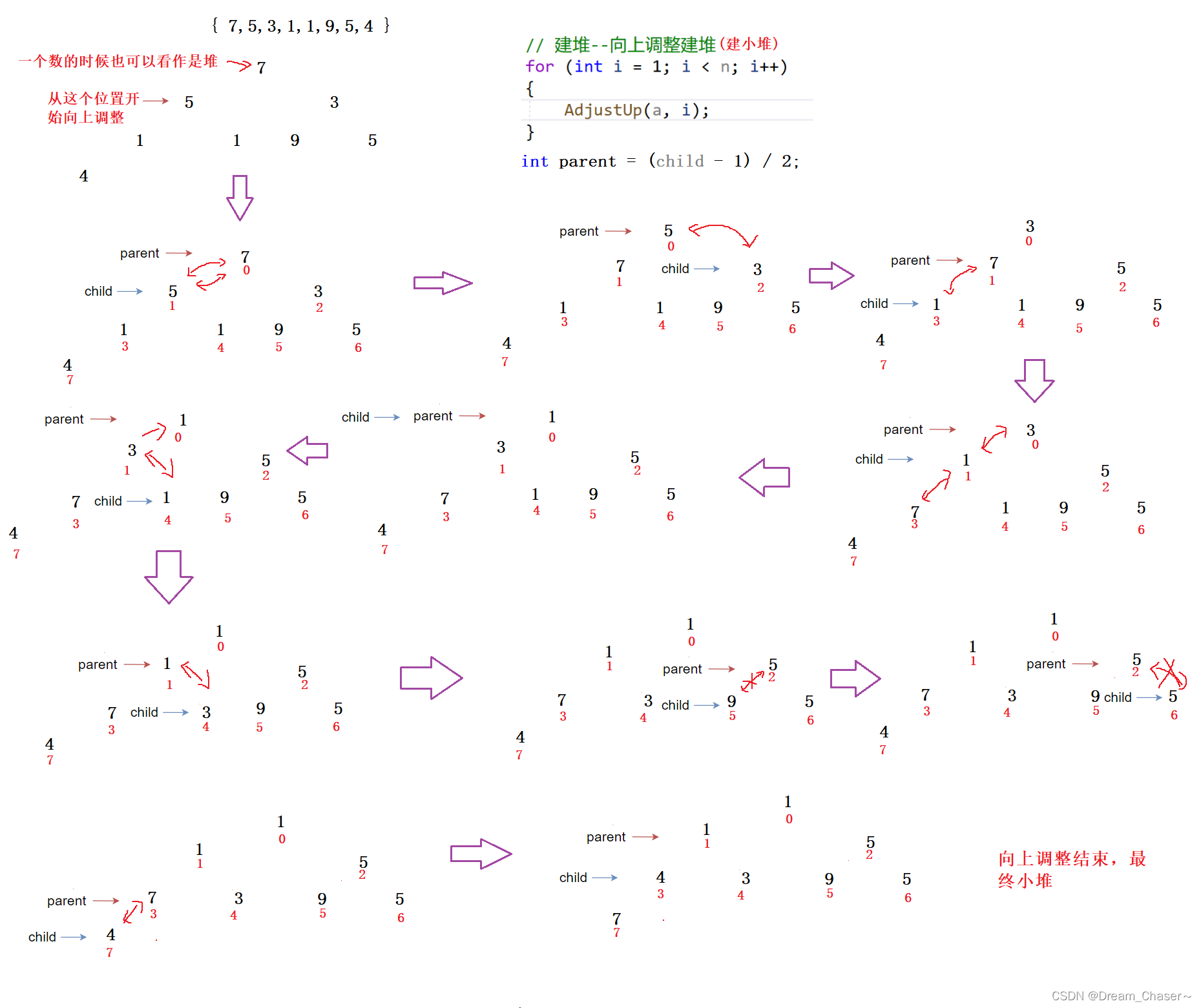
排序：再通过向下调整，变成降序的例子(只演示了一遍的过程，因为篇幅太长了)

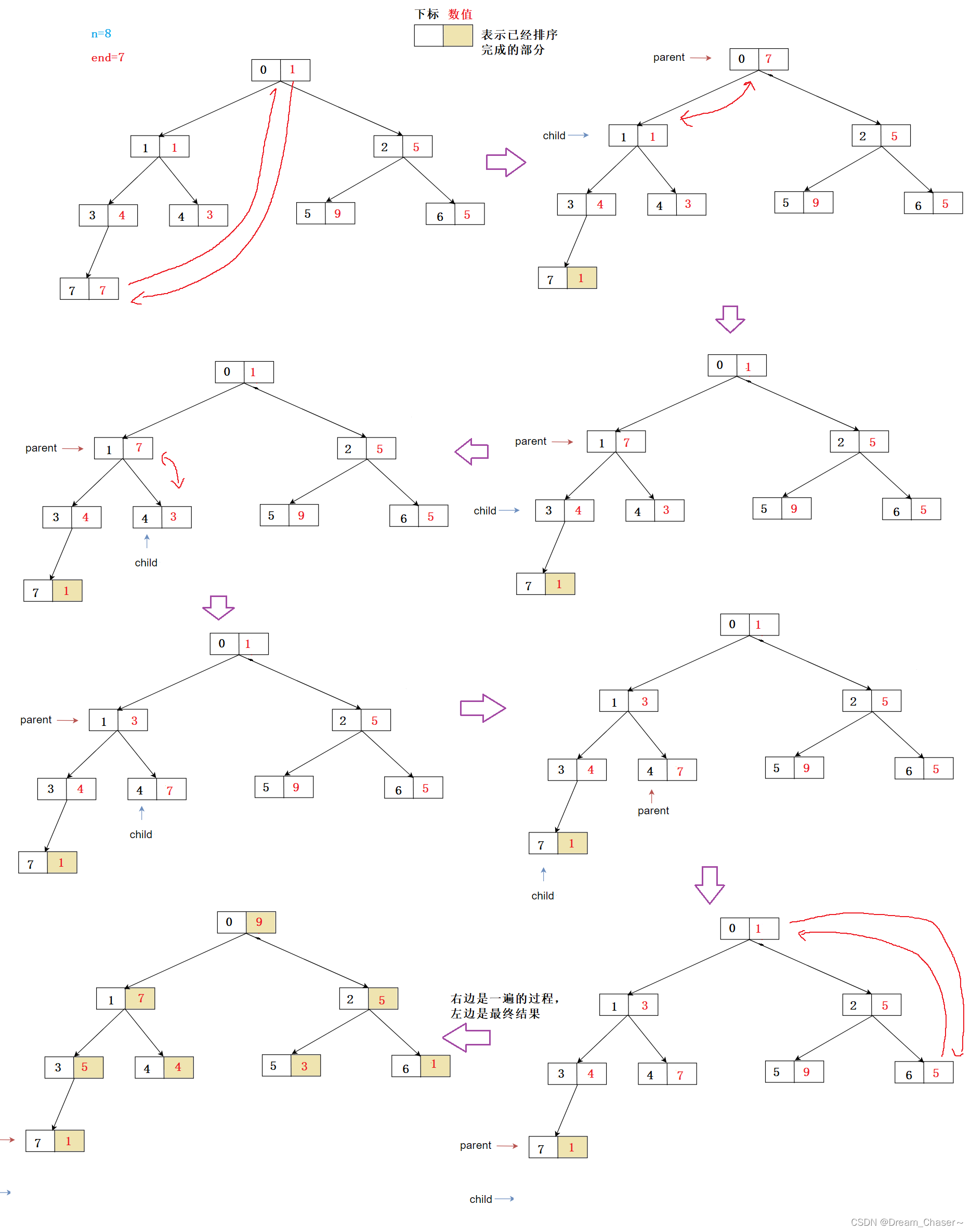
向上调整算法建堆的时间复杂度:O(N):F(N)= (N+1)*(log(N+1)-2)+ 2

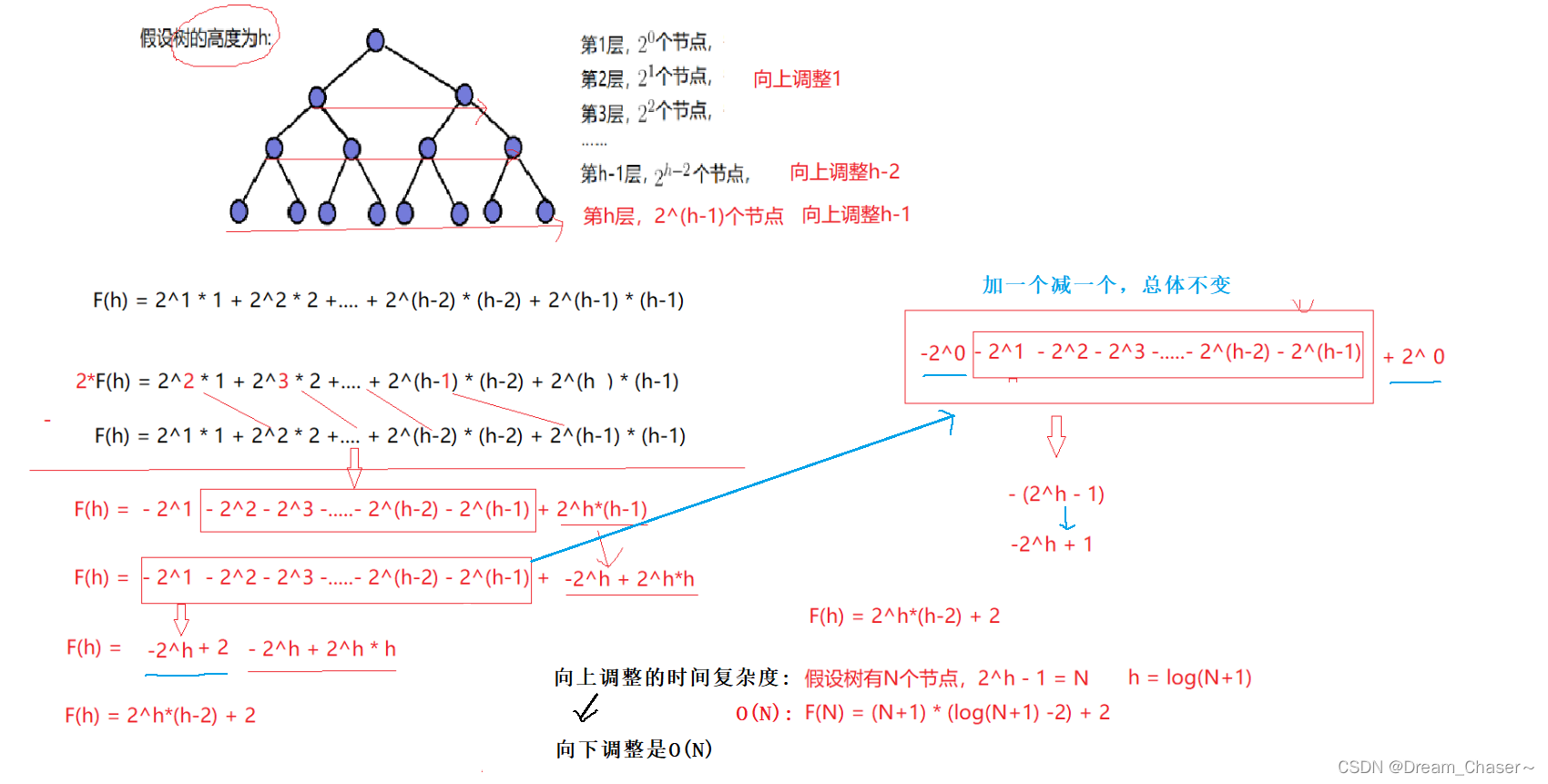
特别注意:向下调整(父节点下标是0)

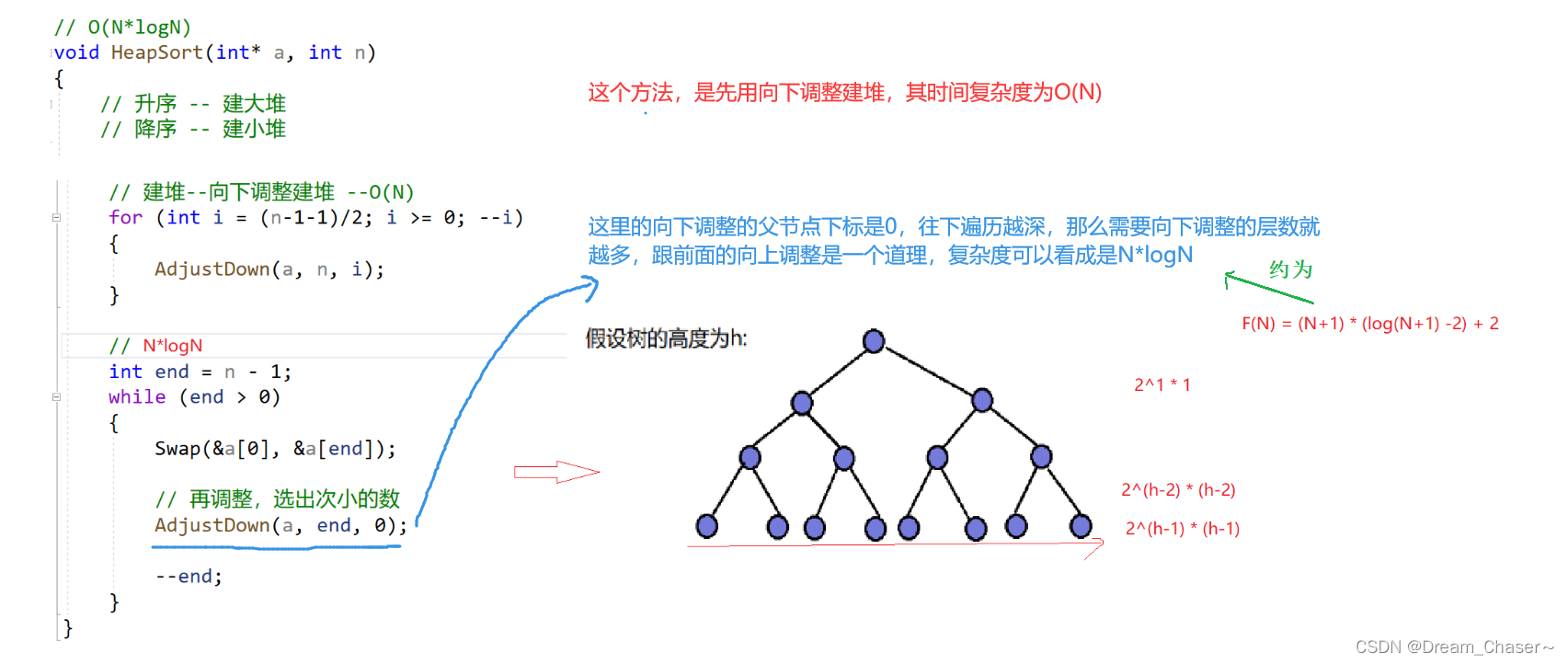
4.1.3向下调整建堆(动图)

动图解析：

向下调整的最终结果:

排序：

这个向下调整的排序结果，跟上面先向上调整，再经过向下调整的排序结果是一样的，跟上面的向下调整的排序思路也是一样的，只是刚开始数据的顺序不一样。

向下调整算法建堆的时间复杂度: O(N)=N - log(N+1)

因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明( 时间复杂度本来看的是近似值，多几个节点不影响最终结果) ：

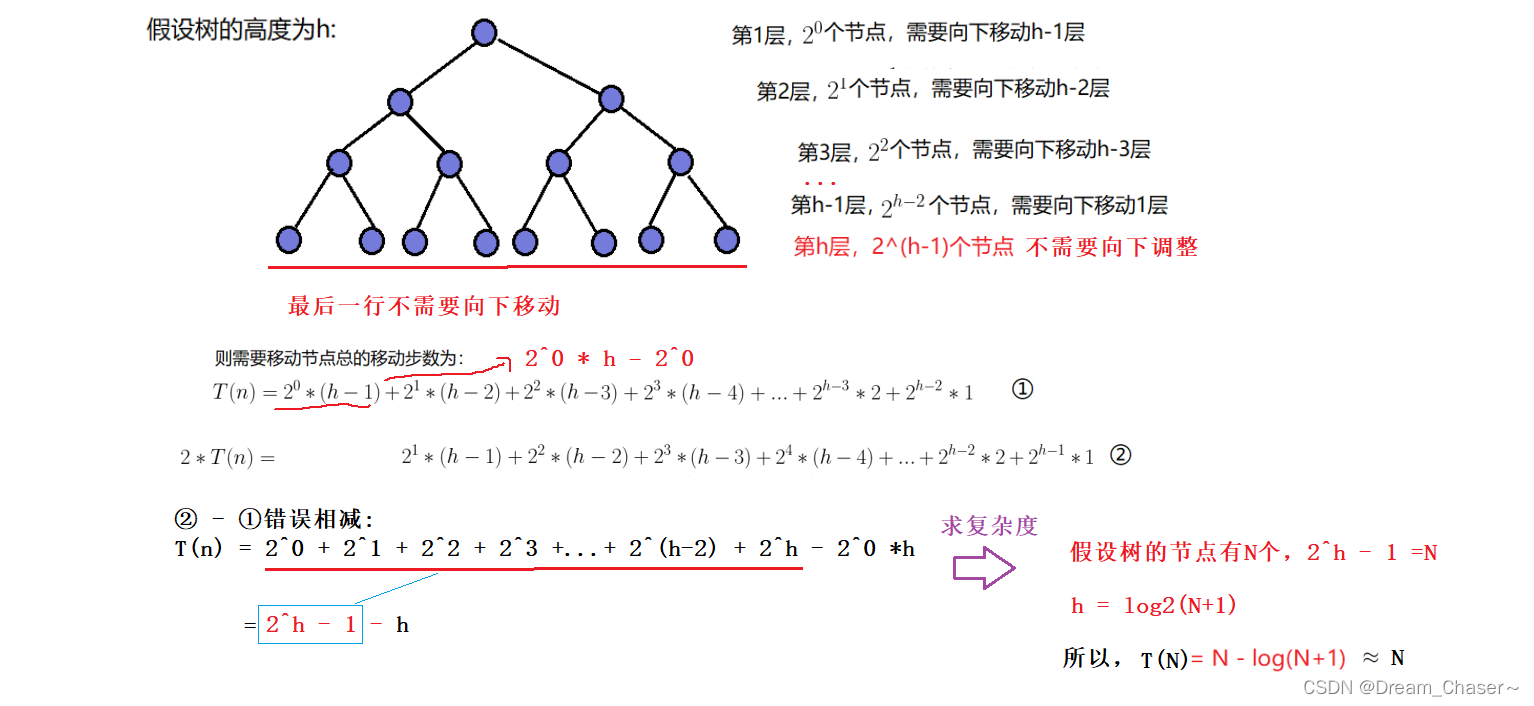因此：建堆的时间复杂度为O(N)。

4.2TOP-K问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决，基本思路如下：

数值间的转换关系:

1G= 1024MB

1024MB = 1024*1024KB

1024*1024KB= 1024*1024*1024Byte 约等于10亿Byte

解决思路:

把这个N建成大堆，PopK次，即可找出最大的前K个有些场景，但是有特殊情况上面的思路解决不了，比如N非常大,假设N是10亿，K是100,解决方法：数据多，数据存在磁盘文件中

具体步骤：

1. 用数据集合中前 K 个元素来建堆

前k个最大的元素，则建小堆
前k个最小的元素，则建大堆

2. 用剩余的 N-K 个元素依次与堆顶元素来比较，不满足则替换堆顶元素

将剩余 N-K 个元素依次与堆顶元素比完之后，堆中剩余的 K 个元素就是所求的前 K 个最小或者最大的元素

4.2.1生成随机数并写入文件

这段代码的目的是生成10000个0到999999之间的随机数，并将它们写入"data.txt"文件中，每个数占一行

void CreateNDate()
{
	// 造数据
	int n = 10000;//并将其赋值为10000,这个变量表示要生成的随机数据的数量
	srand(time(0));//初始化随机数生成器,返回当前时间的秒数，用于生成不同的随机数序列。
	const char* file = "data.txt";//这个变量表示要写入的文件名
	FILE* fin = fopen(file, "w");
	if (fin == NULL)//函数以写入模式打开文件。如果文件打开失败，会输出错误信息并返回
	{
		perror("fopen error");
		return;
	}

	for (size_t i = 0; i < n; ++i)
	{//rand()函数用于生成随机数，%操作符用于限制随机数的范围。
		int x = rand() % 1000000;//循环从0到n-1，每次迭代生成一个随机数x，范围在0到999999之间。
		fprintf(fin, "%d\n", x);//使用fprintf(fin, "%d\n", x)将随机数写入文件。
							    //fprintf()函数用于格式化输出，将随机数写入文件的新行。
	}

	fclose(fin);//使用fclose(fin)关闭文件，确保数据写入完成并释放相关资源。
}

执行：

生成10000个随机数并且范围在0~999999之间

4.2.2建立小堆并比较元素进行合理替换

该函数的目的是从"data.txt"文件中读取数据，并按照从大到小的顺序打印出前k个最大的数。

void PrintTopK(int k)
{
	const char* file = "data.txt";//声明一个指向常量字符的指针file，并将其赋值为"data.txt"。这个变量表示要读取的文件名。
	FILE* fout = fopen(file, "r");//使用fopen(file, "r")函数以读取模式打开文件。如果文件打开失败，会输出错误信息并返回。
	
	if (fout == NULL)
	{
		perror("fopen error");
		return;
	}
	
	//使用malloc(sizeof(int) * k)函数动态分配一个能容纳k个整数的内存空间，
	int* kminheap = (int*)malloc(sizeof(int) * k);
	//返回的指针赋值给kminheap。如果内存分配失败，会输出错误信息并返回。
	if (kminheap == NULL)
	{
		perror("malloc error");
		return;
	}

	for (int i = 0; i < k; i++)
	{//使用循环从文件中读取前k个整数，并将它们存储在kminheap数组中。fscanf()函数用于从文件中读取格式化输入。
		fscanf(fout, "%d", &kminheap[i]);
	}

	// 建小堆
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(kminheap, k, i);
	}

	int val = 0;//声明一个整数变量val，用来存储从文件中读取的下一个整数
	while (!feof(fout))//使用循环从文件中读取剩余的整数，并与小堆的根节点比较。
		//如果读取的整数大于小堆的根节点，则将其替换为根节点，并重新调整小堆。
	{
		fscanf(fout, "%d", &val);
		if (val > kminheap[0])
		{
			kminheap[0] = val;
			AdjustDown(kminheap, k, 0);
		}
	}
	//使用循环打印小堆中的元素，即前k个最大的数
	for (int i = 0; i < k; i++)
	{
		printf("%d ", kminheap[i]);
	}
	//最后，在打印完所有元素后，输出一个换行符
	printf("\n");
}

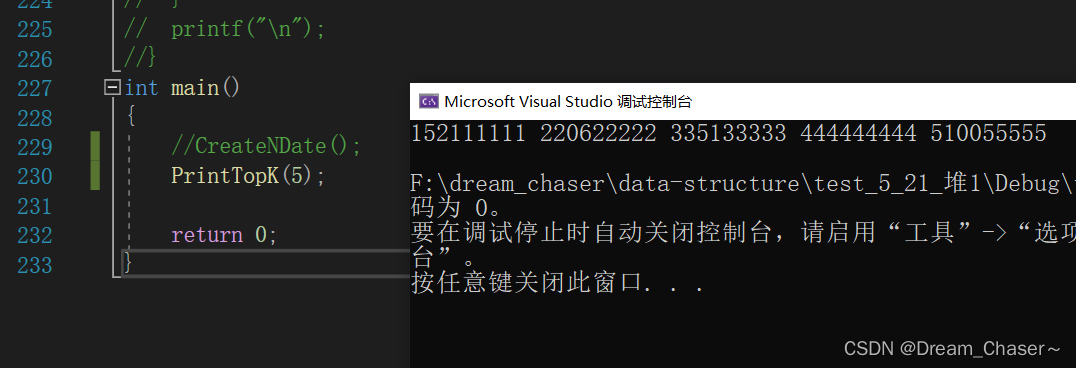
我们执行一下，看看情况如何：

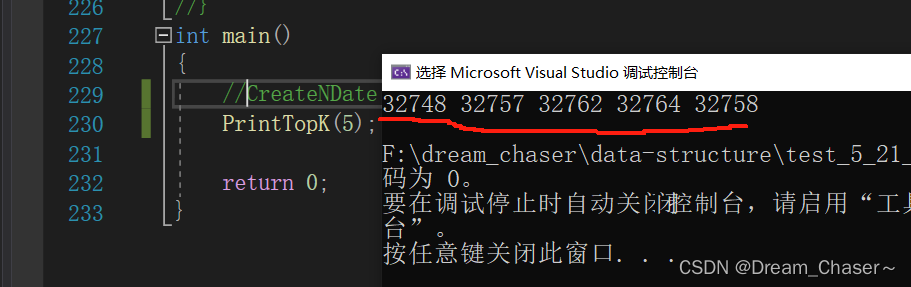
可以看到，这些数据并不好一眼看出建的是小堆的数据，我们可以手动来验证一下，打开文本文件:

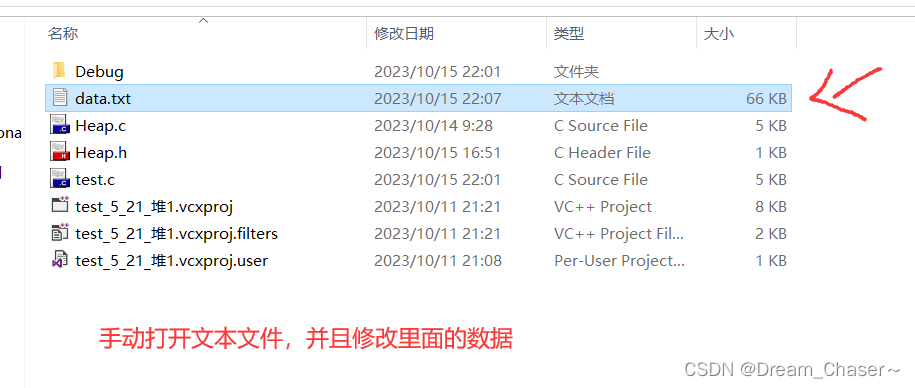
修改的数据明显一点，一眼就可以看出数据大小。

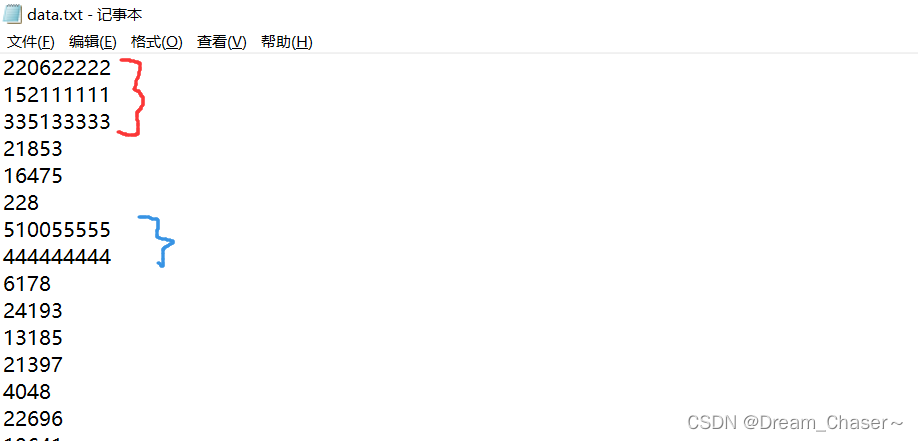排序执行：

5.总代码

test.c

#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"
#include<time.h>

//int main()
//{
//	HP hp;
//	HeapInit(&hp);
//	//int a[] = { 65,100,70,32,50,60 };
//	int b[] = { 100,90,80,70,60,50 };
//	for (int i = 0; i < sizeof(b) / sizeof(int); ++i)
//	{
//		HeapPush(&hp, b[i]);
//	}
//	while (!HeapEmpty(&hp))
//	{
//		int top = HeapTop(&hp);
//		printf("%d\n", top);
//		HeapPop(&hp);
//	}
//	return 0;
//}

//弊端:1.先有一个堆，太麻烦。2.空间复杂度+拷贝数据
//void HeapSort(int* a, int n)
//{
//	HP hp;
//	HeapInit(&hp);
//	//N * logN
//	for (int i = 0; i < n; i++)
//	{
//		HeapPush(&hp,a[i]);
//	}
//	//N * logN
//	int i = 0;
//	while (!HeapEmpty(&hp))
//	{
//		int top = HeapTop(&hp);
//		a[i++] = top;
//		HeapPop(&hp);
//	}
//	
//	HeapDestroy(&hp);
//}
//
//
//int main()
//{
//	int a[] = { 7,8,3,5,1,9,5,4 };
//	HeapSort(a, sizeof(a) / sizeof(int));
//
//	return 0;
//}

//void HeapSort(int* a, int n)
//{
//	//建堆 -- 向上调整
//	/*for (int i = 1; i < n; i++)
//	{
//		AdjustUp(a, i);
//	}*/
//	//建堆  -- 向下调整
//	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
//	{
//		AdjustDown(a, n, i);
//	}
//
//	int end = n - 1;
//	while (end > 0)
//	{
//		Swap(&a[0], &a[end]);
//
//		//再调整
//		AdjustDown(a, end, 0);
//
//		--end;
//	}
//}
//int main()
//{
//	int a[] = { 7,5,3,1,1,9,5,4 };
//	HeapSort(a, sizeof(a) / sizeof(int));
//
//	return 0;
//}
//
//
//这段代码的目的是生成10000个0到999999之间的随机数，并将它们写入"data.txt"文件中，每个数占一行
void CreateNDate()
{
	// 造数据
	int n = 10000;//并将其赋值为10000,这个变量表示要生成的随机数据的数量
	srand(time(0));//初始化随机数生成器,返回当前时间的秒数，用于生成不同的随机数序列。
	const char* file = "data.txt";//这个变量表示要写入的文件名
	FILE* fin = fopen(file, "w"); // 这个地方, 不要写单引号
	if (fin == NULL)//函数以写入模式打开文件。如果文件打开失败，会输出错误信息并返回
	{
		perror("fopen error");
		return;
	}

	for (size_t i = 0; i < n; ++i)
	{//rand()函数用于生成随机数，%操作符用于限制随机数的范围。
		int x = rand() % 1000000;//循环从0到n-1，每次迭代生成一个随机数x，范围在0到999999之间。
		fprintf(fin, "%d\n", x);//使用fprintf(fin, "%d\n", x)将随机数写入文件。
							    //fprintf()函数用于格式化输出，将随机数写入文件的新行。
	}

	fclose(fin);//使用fclose(fin)关闭文件，确保数据写入完成并释放相关资源。
}

//该函数的目的是从"data.txt"文件中读取数据，并按照从大到小的顺序打印出前k个最大的数。
void PrintTopK(int k)
{
	const char* file = "data.txt";//声明一个指向常量字符的指针file，并将其赋值为"data.txt"。这个变量表示要读取的文件名。
	FILE* fout = fopen(file, "r");//使用fopen(file, "r")函数以读取模式打开文件。如果文件打开失败，会输出错误信息并返回。
	
	if (fout == NULL)
	{
		perror("fopen error");
		return;
	}
	
	//使用malloc(sizeof(int) * k)函数动态分配一个能容纳k个整数的内存空间，
	int* kminheap = (int*)malloc(sizeof(int) * k);
	//返回的指针赋值给kminheap。如果内存分配失败，会输出错误信息并返回。
	if (kminheap == NULL)
	{
		perror("malloc error");
		return;
	}

	for (int i = 0; i < k; i++)
	{//使用循环从文件中读取前k个整数，并将它们存储在kminheap数组中。fscanf()函数用于从文件中读取格式化输入。
		fscanf(fout, "%d", &kminheap[i]);
	}

	// 建小堆
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(kminheap, k, i);
	}

	int val = 0;//声明一个整数变量val，用来存储从文件中读取的下一个整数
	while (!feof(fout))//使用循环从文件中读取剩余的整数，并与小堆的根节点比较。
		//如果读取的整数大于小堆的根节点，则将其替换为根节点，并重新调整小堆。
	{
		fscanf(fout, "%d", &val);
		if (val > kminheap[0])
		{
			kminheap[0] = val;
			AdjustDown(kminheap, k, 0);
		}
	}
	//使用循环打印小堆中的元素，即前k个最大的数
	for (int i = 0; i < k; i++)
	{
		printf("%d ", kminheap[i]);
	}
	//最后，在打印完所有元素后，输出一个换行符
	printf("\n");
}


int main()
{
	//CreateNDate();
	PrintTopK(5);

	return 0;
}

Heap.h

#pragma once

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;//有效数据个数
	int capacity;//容量
}HP;

//向上调整
void AdjustUp(HPDataType* a, int child);
//向下调整
void AdjustDown(int* a, int n, int parent);

//堆的初始化s
void HeapInit(HP* php);
// 堆的销毁
void HeapDestroy(HP* php);
// 堆的插入
void HeapPush(HP* PHP, HPDataType x);
// 堆的删除
void HeapPop(HP* php);
// 取堆顶的数据
HPDataType HeapTop(HP* php);
// 堆的判空
bool HeapEmpty(HP* php);
// 堆的数据个数
int HeapSize(HP* php);

Heap.c

void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->capacity = php->size = 0;
}

void HeapDestroy(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}
void Swap(HPDataType* a1, HPDataType* a2)
{
	HPDataType tmp = *a1;
	*a1 = *a2;
	*a2 = tmp;
}
void Swap1(HPDataType* n1, HPDataType* n2)
{
	HPDataType tmp = *n1;
	*n1 = *n2;
	*n2 = tmp;
}
void Swap2(HPDataType* x1, HPDataType* x2)
{
	HPDataType tmp = *x1;
	*x1 = *x2;
	*x2 = tmp;
}



void AdjustUp(int* a, int child)//AdjustUp
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] < a[parent])//小堆< /大堆 >
		{
			Swap1(&a[child], &a[parent]);

			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{		//先判断是否越界的情况下，再判断两个孩子的大小；
		if (child + 1 < n && a[child] > a[child + 1])//假设左孩子小
		{
			child++;
		}

		if (a[child] < a[parent])
		{
			Swap2(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{	//如果空间不够则扩容
		int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, newCapacity * sizeof(HPDataType));
		if (tmp == NULL)
		{
			perror("malloc fail\n");
			return;
		}
		php->a = tmp;
		php->capacity = newCapacity;
	}

	php->a[php->size] = x;
	php->size++;
	AdjustUp(php->a, php->size - 1);
}


void HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));

	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;

	AdjustDown(php->a, php->size, 0);
}


HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));

	return php->a[0];
}

bool HeapEmpty(HP* php)
{
	assert(php);

	return php->size == 0;
}

int HeapSize(HP* php)
{
	assert(php);

	return php->size;
}

本篇文章到此结束，如有错误，欢迎更正，感谢来访！