目录
- 1. 二分查找
- 2. 补充:二进制运算
- 2.1 十进制与二进制的相互转换
- 2.1.1 十进制转二进制
- 2.1.2 二进制转十进制
- 2.2 机器数 真值
- 2.3 原码 补码 反码
- 2.4 二进制的加减乘除
- 2.5 移位运算
1. 二分查找
思想: 有序数组,从中找值
实现:
-
while 循环:时间复杂度:log(n)
public static int binarySearch01(int[] arr, int target) { int i = 0; int j = arr.length - 1; // <= 是因为目标值可能在 0 或 arr.length - 1 索引处 while (i <= j) { // 用移位运算防止溢出 int mid = (i + j) >>> 1; if ( target < arr[mid]) { j = mid - 1; } else if (arr[mid] < target){ i = mid + 1; } else { return mid; } } return -1; }优化:把 j 只作为一个右边界,不能指向目标值
public static int binarySearch02(int[] arr, int target) { int i = 0; int j = arr.length; // 这里如果使用 i <= j,会导致查找不存在的元素的时候出现死循环 while (i < j) { int mid = (i + j) >>> 1; if (arr[mid] > target) { j = mid; } else if (arr[mid] < target){ i = mid + 1; } else { return mid; } } return -1; }分析: 往左查找的消耗是往右查找消耗的 1/2,不均衡。(因为往右查找需要比较两次 if)
优化:平均两侧查找消耗public static int binarySearch04(int[] arr, int target) { int i = 0; int j = arr.length; while (1 < j - i) { int mid = (i + j) >>> 1; if (target < arr[mid]) { j = mid; } else { // 这里不能 + 1了,如果目标值就在中间,就找不到了 i = mid; } } if (arr[i] == target) { return i; } return -1; }利用 api 写个二分查找,找到目标值就返回索引 + 数组,找不到就插入再返回
public static Map<Integer, int[]> binarySearch05(int[] arr, int target) { int i = Arrays.binarySearch(arr, target); Map<Integer, int[]> res = new HashMap<>(); if (0 < i) { res.put(i, arr); return res; } int targetIndex = abs(i + 1); int[] arr0 = new int[arr.length + 1]; System.arraycopy(arr, 0, arr0, 0, targetIndex); arr0[targetIndex] = target; System.arraycopy(arr, targetIndex, arr0, targetIndex + 1, arr.length - targetIndex); res.put(targetIndex, arr0); return res; } -
Arrays.binarySearch包含多种类型的数据,这里看 int 的:
binarySearch0的返回值 = - 插入点 - 1
为什么不直接返回 -插入点?答:为了防止插入点为0出现歧义public static int binarySearch(int[] a, int key) { return binarySearch0(a, 0, a.length, key); } private static int binarySearch0(int[] a, int fromIndex, int toIndex, int key) { int low = fromIndex; int high = toIndex - 1; while (low <= high) { int mid = (low + high) >>> 1; int midVal = a[mid]; if (midVal < key) low = mid + 1; else if (midVal > key) high = mid - 1; else return mid; // key found } return -(low + 1); // key not found. } -
二分查找返回最左/最右的索引(相同元素情况)
/** * @Desc falg = -1 返回最左索引,flag = 1 返回最右索引 */ public static int binarySearchLeftOrRight(int[] arr, int target, int flag) { int i = 0; int j = arr.length - 1; int index = -1; while (i <= j) { int mid = (i + j) >>> 1; if (target < arr[mid]) { j = mid - 1; } else if (arr[mid] < target) { i = mid + 1; } else { index = mid; if (1 == flag) { i = mid + 1; } else { j = mid - 1; } } } return index; } -
优化: 二分查找返回最左/最右的索引(相同元素情况)
/** * @param flag = -1 返回最左索引, = 1 返回最右索引 * @return int 存在,返回对应索引,不存在,返回 - 插入点 - 1 */ public static int binarySearchLeftOrRight(int[] arr, int target, int flag) { int i = 0; int j = arr.length - 1; while (i <= j) { int mid = (i + j) >>> 1; if (flag == 1 ? target < arr[mid] : target <= arr[mid]) { j = mid - 1; } else { i = mid + 1; } } int index = flag == 1 ? i - 1 : i; if (target == arr[index]) { return index; } return - index - 1; }
2. 补充:二进制运算
2.1 十进制与二进制的相互转换
2.1.1 十进制转二进制
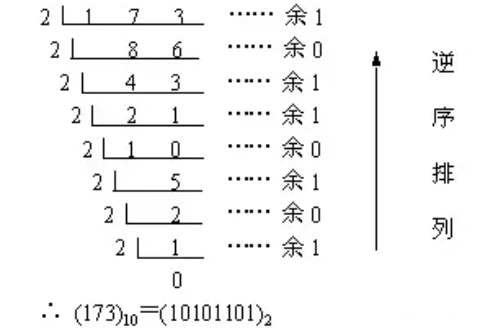
- 方法:短除法
- 整数:
逆序排列
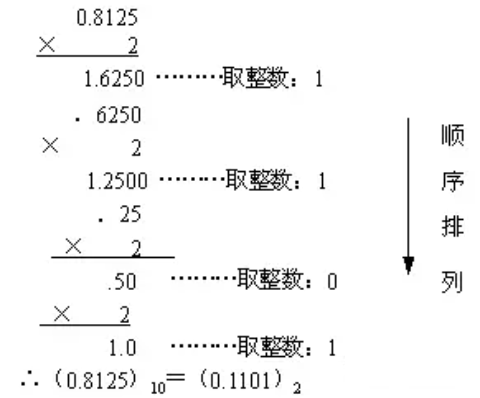
- 小数:
顺序排列
原则: 一直转换到小数部分清零为止
- 整数:
思考: 有些小数部分是无法清零的该怎么处理?
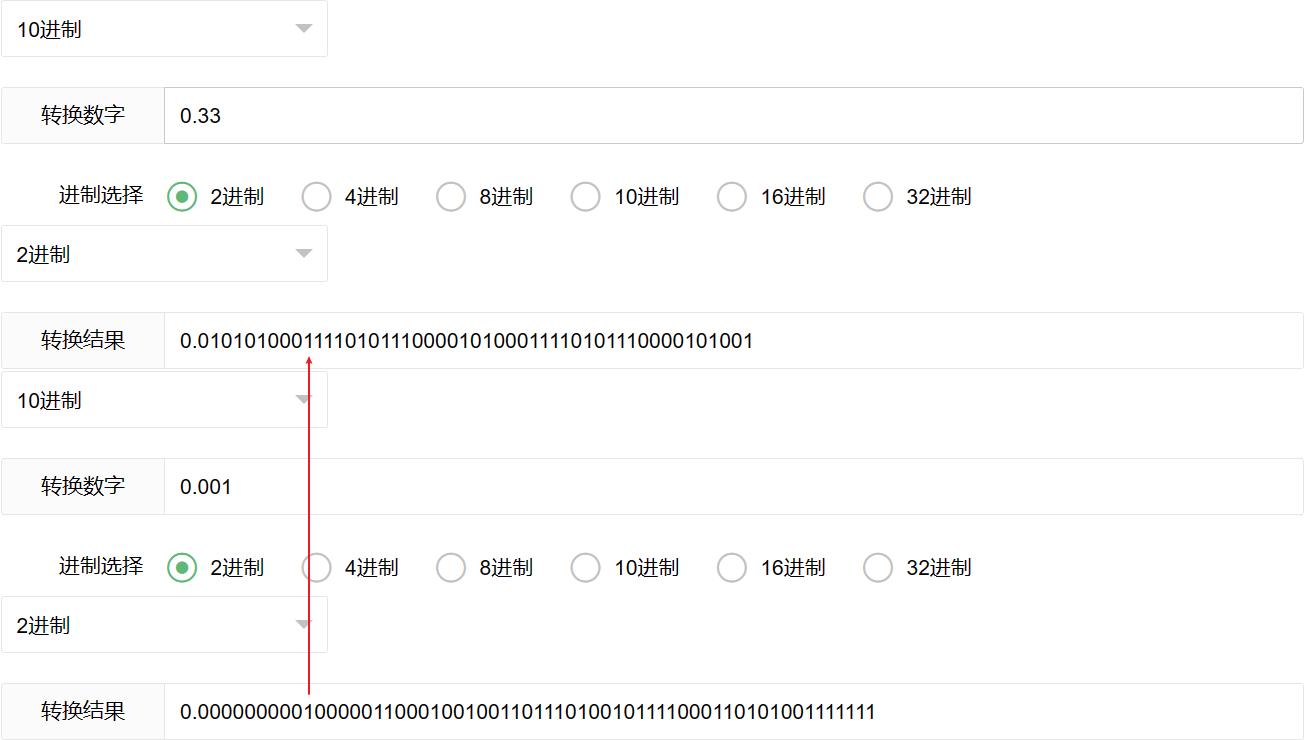
这时候就要引入误差/精度了,比如说:0.33转换成二进制,误差小于1‰,那么我假设转换后的结果为 x,那么要求就是: |x - 0.33| < 1‰,即 0.319 < x < 0.331。
那么如何快速计算出结果呢?
进制转换工具
所以 x 取 0.0101010001 就OK了
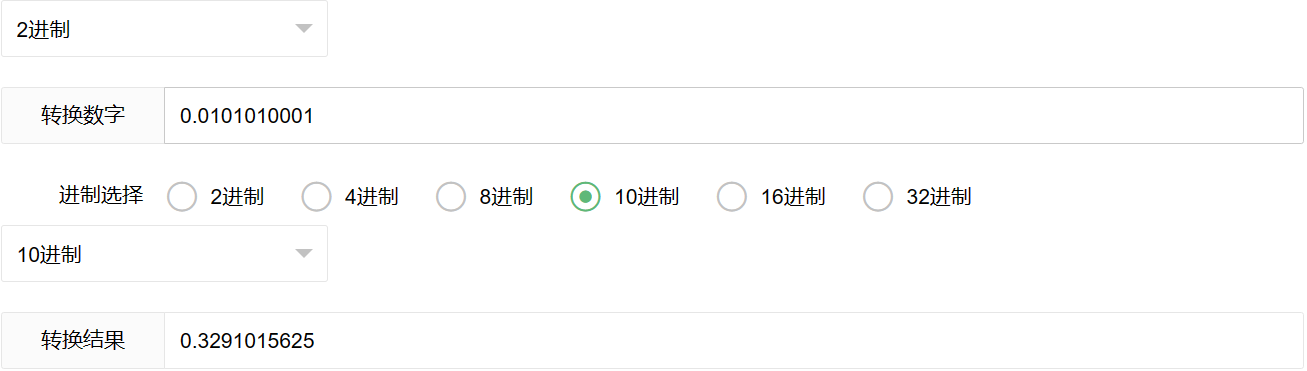
验证一下:
没问题。
2.1.2 二进制转十进制
- 整数:10101101 → 173
向右减权1*2^7 + 0*2^6 + 1*2^5 + 0*2^4 + 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0 - 小数:0.1101 → 0.8125
向右减权1*2^-1 + 1*2^-2 + 0*2^-3 + 1+2^-4
2.2 机器数 真值
机器数: 数字在计算机中的二进制表示形式。在计算机中,数字以二进制形式存储和处理。机器数的最高位是符号位,用于表示数字的正负。正数的符号位为0,负数的符号位为1。机器数的大小受到计算机字长的限制,字长决定了机器数的表示范围。
// 不同位的计算机中表示 5
00000101 # 8位
00000000 00000000 00000000 00000101 # 32位
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000101 # 64位
64位计算机能一次读8byte,32位能一次读 4byte,可通过 cmd 输入
systeminfo查看计算机参数
比如某机器的机器数大小是 2 byte,那么它存储数字 5 的机器数就是:0000 0101,最左边的 0 表示正数,其表示 -5 的机器数就是 1000 0101
真值: 带符号位的机器数对应的真正数值,可以通过将机器数转换为十进制数来获得。
比如:机器数 1000 0101 的真值是 -5,0000 0101 的真值是 5。
2.3 原码 补码 反码
原码: 最高位表示符号位,其余位表示数值的绝对值,和机器数一个意思。
反码: 正数的反码和原码相同,负数的反码是在其原码的基础上,符号位不变,其余各位取反。
比如:正数+5的反码和原码都是00000101,负数-5的反码是11111010 。
补码: 正数的补码和原码相同,负数的补码是在其反码的基础上加1。
比如:正数+5的补码和原码都是00000101,负数-5的补码是11111011。
小结一下:对于正数:原码 = 反码 = 补码;对于负数:反码 = 原码标志位不变,其余取反(1变成0,0变成1),补码 = 反码 + 1。
补充:负数的补码转原码
- 先取反
- 然后 + 1
2.4 二进制的加减乘除
加法: 正数 + 负数 我们放到减法里面说
- 方法:从右往左加,逢二进一
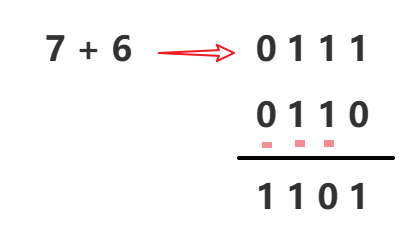
减法:
- 方法:都换成补码,然后相加,相加的结果就是答案
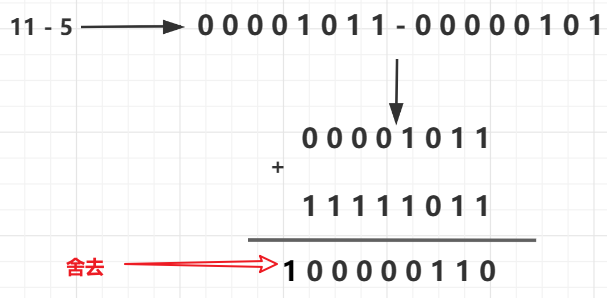
因为我们是在 8 位二进制里面做加减,所以超出(溢出)的 1 要舍去
乘法:
- 正数:与十进制一样,按位相乘,然后相加
- 负数:摘掉标志位,然后相乘,最后根据两个符号位来判断正负
除法:
- 正数:正数:与十进制一样,按位相除(如果被除数的最高位小于除数的最高位,则除法运算结束。被除数的剩余位数即为余数)
- 负数:负数取补码,然后相除
注意:进制负数除法的结果可能是有限的,也可能是无限循环的。在实际计算中,可能需要根据具体情况进行舍入或截断
2.5 移位运算
二进制移位运算:
<<左移:将一个数的二进制表示向左移动指定的位数,右侧用0填充

可以把<<看做是*2操作>>右移:将一个数的二进制表示向右移动指定的位数,正数高位用0填充,负数高位用1填充

可以把>>看做是/2操作,一直右移,正数会变成 0,负数会变成 -1(为了保证它是负数,所以会补个 1)>>>无符号右移位,不管正数还是负数,高位都用0补齐
注意事项1: 在做移位运算的时候要考虑当前类型的大小,如下:
声明一个 int 整型 -11、11 -11(int) >>> 2 : 原二进制:11111111111111111111111111110101 二进制: 111111111111111111111111111101 十进制: 1073741821 11(int) << 31 : 原二进制: 1011 二进制: 10000000000000000000000000000000 十进制: -2147483648 11(int) << 32 : 原二进制: 1011 二进制: 1011 十进制: 11注意事项2: Java 中会将最高位看做符号位!,所以当数值 > 2^31 的时候,最高位会被当做符号位 1,从而编程负数。
public static void main(String[] args) { int i = (int) pow(2, 31); int j = 1; System.out.println(i); System.out.println(Integer.toBinaryString(i)); System.out.println(i + j); System.out.println(Integer.toBinaryString(i + j)); System.out.println( (i + j) / 2 ); System.out.println( (i + j) >>> 1); }