一、前言
还记得在很久以前不知道什么时候,看到过一个TA的面经,里面提到了四元数和万向锁,当时自己也查了一些资料,但是看的也是云里雾里,恰巧这两天学校的动画原理课讲到了这,打算整理一下做个小结。
二、方位的表达方式
方位的表达方式有很多种,它们各有优缺点,所以每种方式都不能算是很完美,包括四元数也是,但四元数的提出是为了解决方位的插值问题,所以只需要它有这个优点就够了。我们本篇主要探讨的问题也正是方位的插值问题。
以下是常用的方位表示形式
矩阵形式
Fixed Angle形式(参考世界坐标系)
Euler Angle形式(参考局部坐标系)
角度位移形式(Angle and Axis)
四元数形式
1.矩阵形式
熟悉图形变换的我们知道,用矩阵可以表示旋转,并且旋转矩阵一定是正交矩阵,所以旋转矩阵有一个很好的性质就是自身的逆等于自身的转置。那么矩阵自然也可以用在方位的表达中。但如果用矩阵的方位表达形式进行插值呢?下图举一个例子为绕Z轴的旋转矩阵,假设我们从θ=90°旋转到θ=-90°。
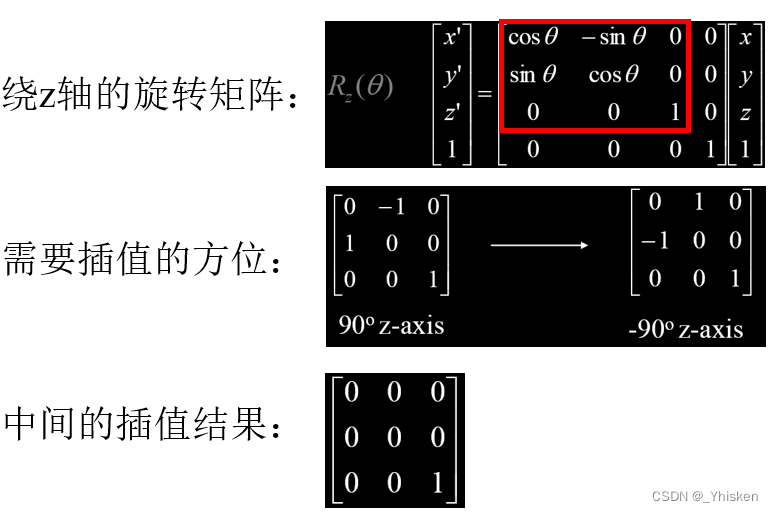
那么得到初始状态的方位矩阵和最终状态的方位矩阵如图所示,当进行中间插值时我们发现出现了问题。得到的插值结果明显不是一个旋转矩阵,也失去了旋转矩阵特有的正交性。所以对于关键帧的方位插值我们显然不能直接使用矩阵形式。
2.Fixed Angle形式(参考世界坐标系)
Fixed Angle其实就是以世界坐标为参考系下进行的方位表达,世界坐标系静止不动由此得到不同方位唯一的表示方法。Fixed Angle进行方位表达时按照固定顺序围绕世界坐标系的坐标轴旋转3次,最常用的为x,y,z顺序(θx,θy,θz)。在插值时需要对三个角度分别进行插值。当然,无论什么形式,我们最终都是要转换成矩阵形式在计算机中计算的,Fixed Angle当然也不例外。
接下来我们看一个例子,看看Fixed Angle能不能完美的实现方位的插值。
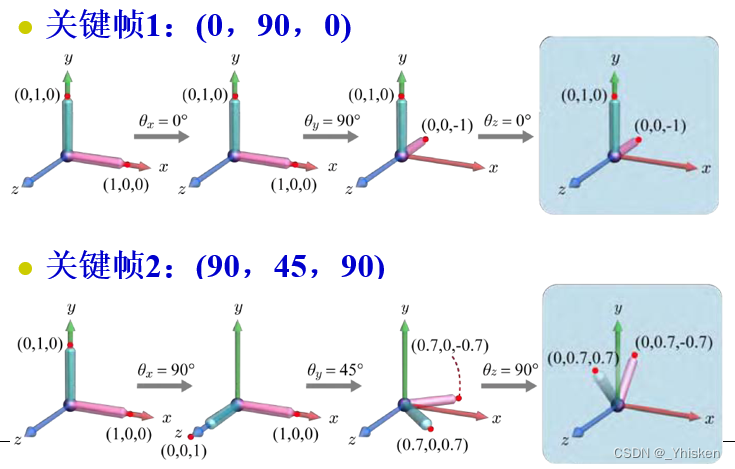
如上图关键帧1和关键帧2,我们选取关键帧1为初始状态,关键帧2为终止状态,那么我们的理想情况是进行插值之后,关键帧1可以平滑的过度到关键帧2的姿态。那么实际情况是不是这样呢?我们取中间帧看一下就知道了。
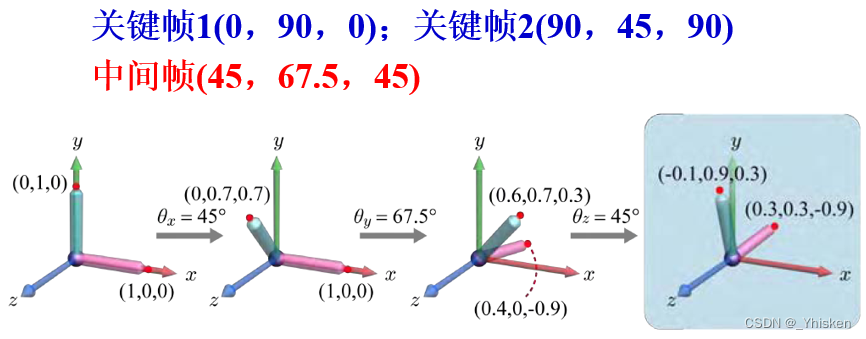
可以看到取中间帧时,物体在三个方向上的旋转角度分量分别是45°,67.5°,45°。也就是说在插值的过程中物体并不是仅仅由绕x轴旋转就从关键帧1过度到关键帧2的,它总会在中间 “扭” 一下。这种现象被称为“死锁”或“万向锁”。之所以被称为万向锁,是因为在万向节装置中,当两个旋转轴重合时,万向节会损失一个方向的自由度,如下图。
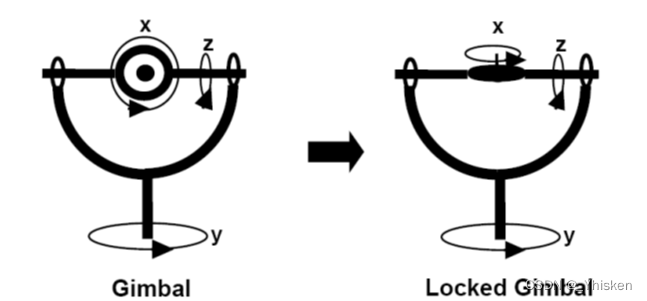
对于上面的例子,Fixed Angle解决死锁的方案是将关键帧1(0, 90, 0)表示为(90, 90, 90),这样经过插值之后中间帧就是(90, 67.5, 90),但显然这样做起来很麻烦,并且无法保证方位表达的唯一性。
3.Euler Angle形式(参考局部坐标系)
Euler Angle,也就是欧拉角。本质上和Fixed Angle其实是一个东西,只不过Fixd Angle是以世界坐标为参考系,而欧拉角是以物体自身为参考系。
简单地说,就是将物体局部坐标系与世界坐标系重合;世界坐标系静止不动,局部坐标系与物体绑定,然后以局部坐标系为参考,对物体进行旋转(每次旋转时,局部坐标系随物体一起旋转)。
既然说了Fixed Angle和Euler Angle本质上是一样的只是参考系不同,那么我们就完全可以把它们之间互相转换,它们完全是逆向等价的。

4.角度位移形式(Angle and Axis)
欧拉旋转定理
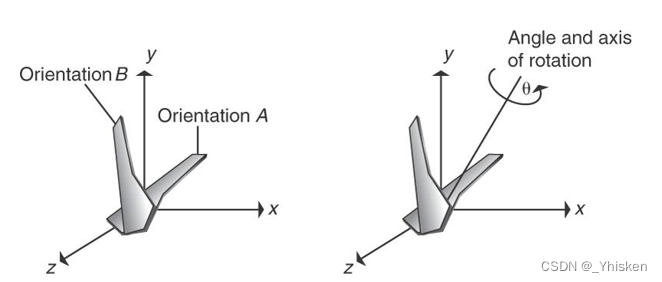
某个物体的两个空间朝向之间,存在唯一的、简单稳定的、绕某一空间轴的旋转变换。
角度:θ , 旋转轴(单位向量):(Ax, Ay, Az)
这很好想,我们知道旋转肯定会产生一个圆环面,那么面就一定有一个法向量,也就是旋转轴对于的方向。
Angle and Axis对方位的表示是使用一个旋转轴(单位向量)和一个角度值来表示物体的朝向,如(θ, Ax, Ay, Az)。插值方法则是对旋转轴和旋转角度分别进行插值计算。
当然了,和其它方法一样,Angle and Axis仍然需要把插值后的结果转换成矩阵形式在计算机里表示。角度位移形式转换为矩阵的公式如下。

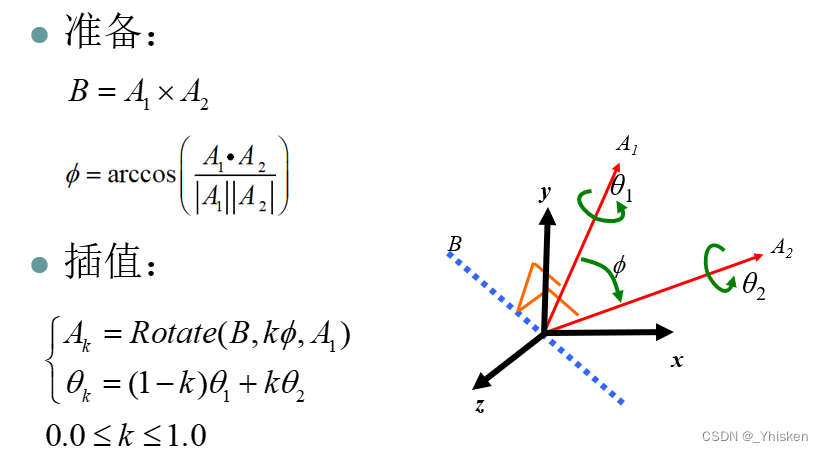
同样的,我们举一个例子,上图所示A1单位向量为初始状态,现在要通过变换把它变为A2单位向量的最终状态。根据欧拉旋转定理,我们可以求出唯一旋转轴B,只需要A1xA2也就是叉乘就可以了,知道了旋转角度,旋转轴,单位向量,我们自然可以对旋转的角度Φ(由arccos得到)进行插值。同时也就可以对单位向量自身的旋转θ进行插值,如上图所示。
显然Angle and Axis不会产生死锁问题。但有一个问题就是Angle and Axis不适合级联表示。比如由初始状态,首先旋转(θ1, Ax1, Ay1, Az1),然后旋转(θ2, Ax2, Ay2, Az2),我们很难知道它相当于由初始状态旋转了多少。
三、四元数
1.用复数表示二维旋转
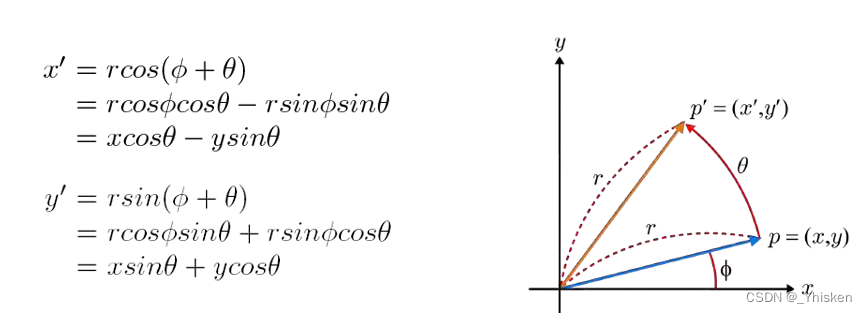
学过线性代数的我们应该很容易就能写出这个旋转的方程表达式。可以很容易的看到在二维平面内逆时针旋转θ,x和y对应的系数关系。
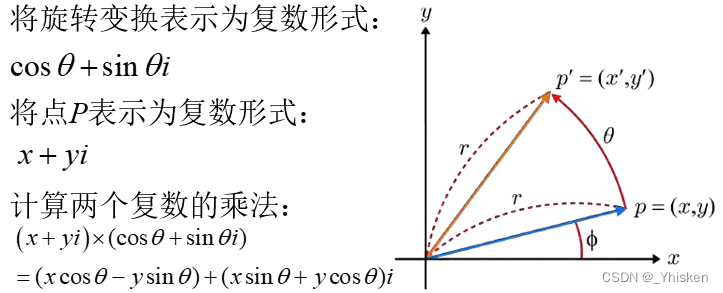
而如果将xy平面转为复数的二维平面,我们就可以把旋转表示成为两个复数的乘法,如上图所示。这时我们发现,复数乘法结果得到的实部就是旋转后的x坐标x',得到的虚部就是旋转后的y坐标y'。 于是我们发现,我们完全可以用复数表示二维平面内的旋转。
将旋转角度θ表示为复数形式:cosθ+sinθi
将二维平面上的点表示为复数形式:x+yi
二者相乘后的结果表示旋转后的点坐标。实部为x坐标,虚部为y坐标。
2.四元数基本概念
四元数顾名思义就是由一个实部和三个虚部构成的。
例如四元数 (a, b, c, d) = a + bi + cj + dk
(1)加减法
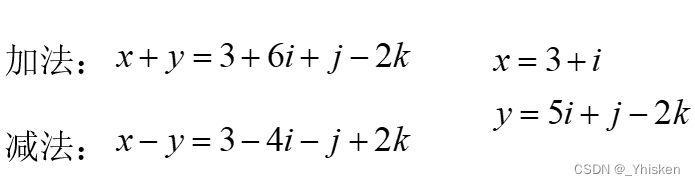
加减法遵循复数,对应实部,虚部相加减的规则。
(2)乘法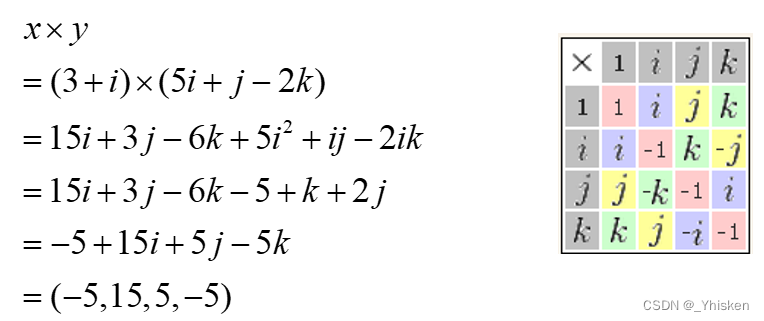
乘法满足分配律,但不满足交换律。 上图右为i,j,k对应的乘积结果表。
(3)点乘
四元数的点乘可以直接当成四维向量的点乘,对应位相乘再加和即可。
(4)其它基本概念
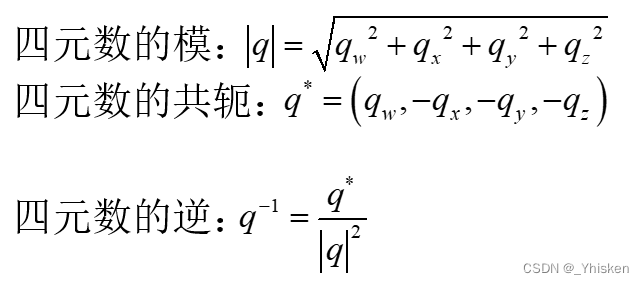
3.四元数表示三维空间旋转
那么如何把四元数对应到三维空间的旋转呢
现在假设已知:
三维空间中一点v=(vx,vy,vz),绕单位轴向量u=(ux,uy,uz)旋转θ度。
我们需要先对点和旋转角度进行处理,把它们转化位四元数。
将点v转化为四元数:p=(0, vx,vy,vz),
将旋转参数转化为单位四元数q:![]()
那么计算公式:![]()
最后提取旋转变换的结果:p’的实部为0,p’的虚部为旋转后的结果。
总结:
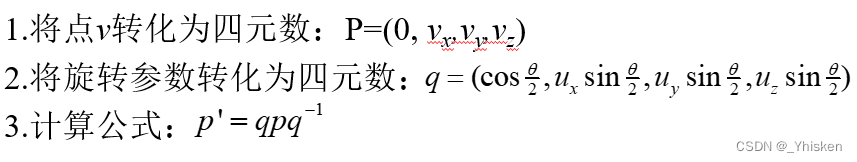
总的来说,单位四元数相当于四维空间中的一个单位球体。它上面的每一个点定义了三维空间中的一个旋转变换。
4.四元数和其他形式的互相转化
(1)四元数转为矩阵

(2)Fixed Angle转为四元数

(3)四元数转为Fixed Angle

5.四元数的优点
(1)结合律表示级联变换
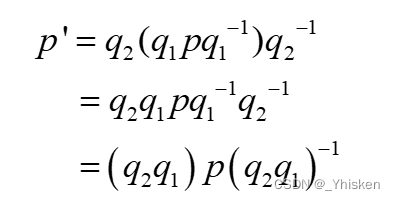
先对p进行q1变换,再进行q2变换,等价于把q1q2合起来一起做变换如上图所示。
(2)适合插值
对于三维空间中的两个方位,首先,将它们表示为四元数形式:
q1= (qx1 , qy1 , qz1 , qw1)
q2= (qx2 , qy2 , qz2 , qw2)
然后,对这两个四元数进行插值即可。
四、四元数插值需要考虑的问题
1.插值点选取
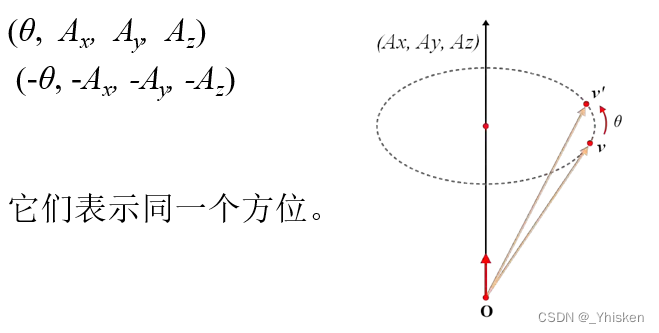
对于上图所示的情况,对单位向量θ,旋转(θ, Ax, Ay, Az) 和 对单位向量-θ旋转l (-θ, -Ax, -Ay, -Az)表示的方位是相同的。并且,两个单位四元数q和-q,它们也表示同一个旋转方位。
证明如下:

2.线性插值问题
对于下图插值公式
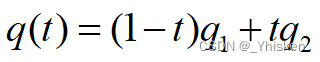
表示旋转的四元数必须是单位长度的: |q|=1。
其次,插值后的四元数不是单位长度的,需要对插值结果进行归一化。如下图所示
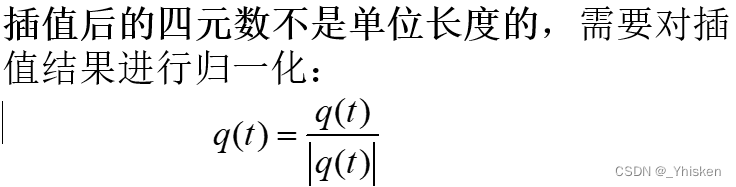
3.球面线性插值
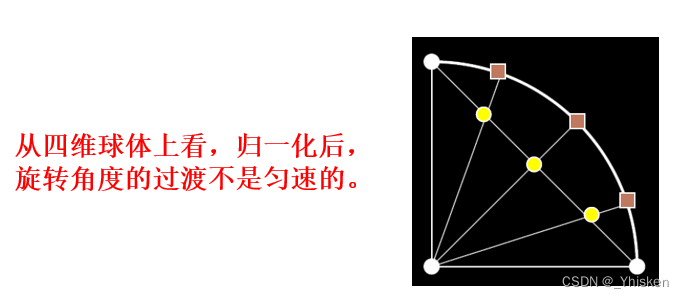
但仍然有问题,我们线性插值得到的结果经过归一化映射到球面上之后我们会发现,角度的变化其实并不是均匀的,显然我们不能对最终的值直接进行线性插值,而是要对角度进行球面线性插值,经过推导,我们可以得到如下图的球面线性插值公式。
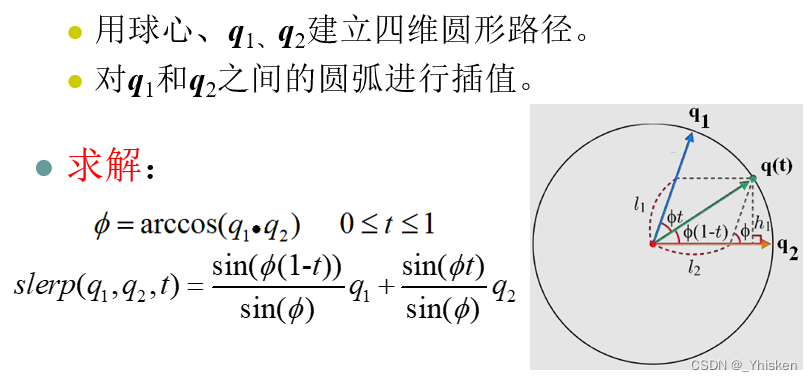
球面线性插值的特性
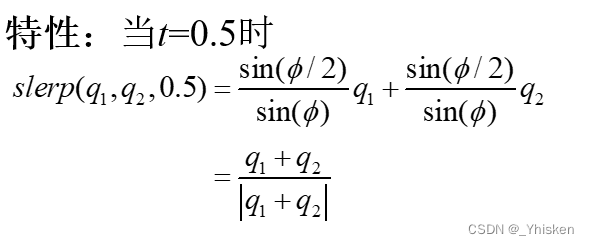
4.Bezier球面线性插值
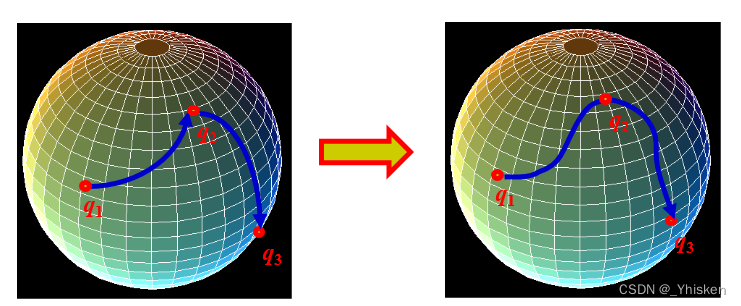
对于多个四元数方位的过渡动画,球面线性插值存在一阶不连续问题。也就是方位过度形成的曲线并不连续,或者说并不平滑。这个问题我们显然很熟悉了,我们完全可以用Bezier曲线去进行平滑的过度。
我们需要根据给定的一系列四元数,在四维球面上构建分段三次Bezier样条线,沿着样条线进行四元数插值即可。
五、结语
本文从比较High Level的层面上总结了一下各种表达方位的方式,涉及介绍较多,公式推导较少,关于一些详细的公式推导可以参考其它文章,有很多大佬写了很多非常好的推导过程可以参考,有兴趣的朋友可以自行学习。
三维旋转:欧拉角、四元数、旋转矩阵、轴角之间的转换 - 知乎 (zhihu.com)【Unity编程】欧拉角与万向节死锁(图文版)-CSDN博客
在学习GAMES101的时候,我曾记得闫令琪老师说过的一句话,我们学东西分为Why,What,How这么几个步骤,How这个步骤往往是花费时间最多的,但是往往其实是最不重要的。我同样觉得,我们着重学习的应该是这些提出这些想法的创意和解决问题的思路,而不单单是公式的推导,当然并不是说推导不重要,而是我常常在想,如果把学完的知识全部忘掉,我应该剩下什么,我觉得那就是最重要的东西,对我而言,那就是解决问题思考问题的能力和对未知的好奇心。