2.1随机变量
强化学习中会经常用到两个概念: 随机变量、 观测值。
本书用大写字母表示随机变量,小写字母表示观测值,避免造成混淆。

下面我们定义概率质量函数(probability mass function,缩写 PMF)和概率密度函数(probability density function,缩写 PDF)
- 概率质量函数(PMF)描述一个离散概率分布——即变量的取值范围 X 是个离散
集合。
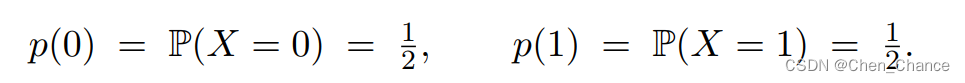
- 概率密度函数(PDF)描述一个连续概率分布——即变量的取值范围 X 是个连续集合。
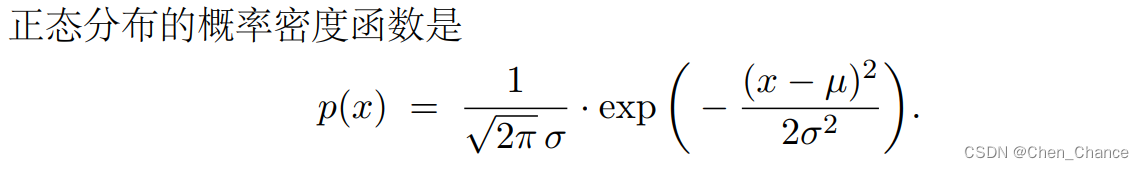
注意,跟离散分布不同,连续分布的 p(x)不等于 P(X = x)。概率密度函数有这样的性质:
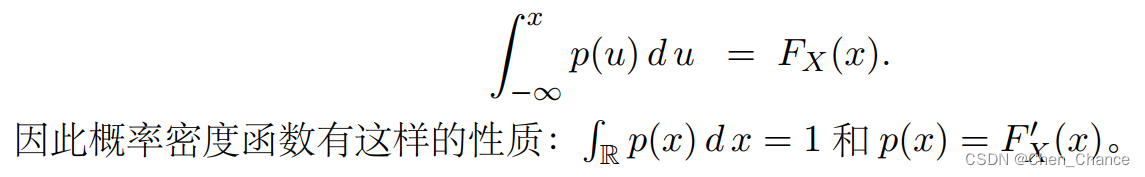
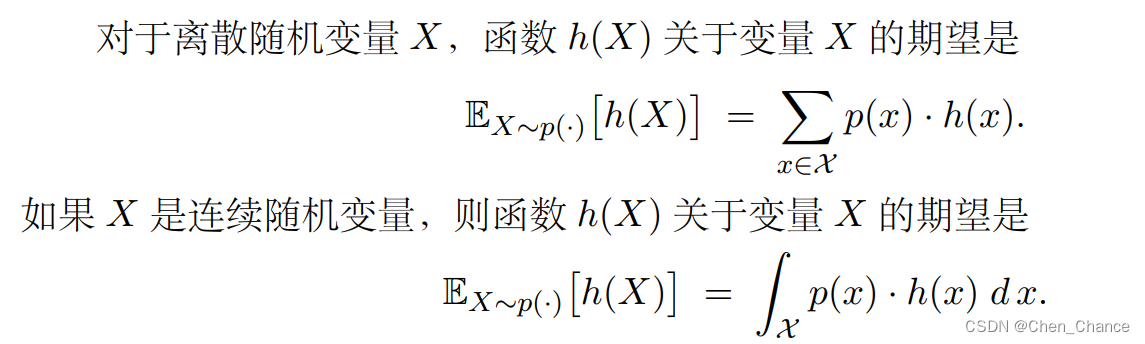

2.2蒙特卡洛估计
蒙特卡洛(Monte Carlo)是一大类随机算法(randomized algorithms)的总称,它们通过随机样本来估算真实值。本节用几个例子讲解蒙特卡洛算法。
2.2.1 例一:近似 π \pi π 值


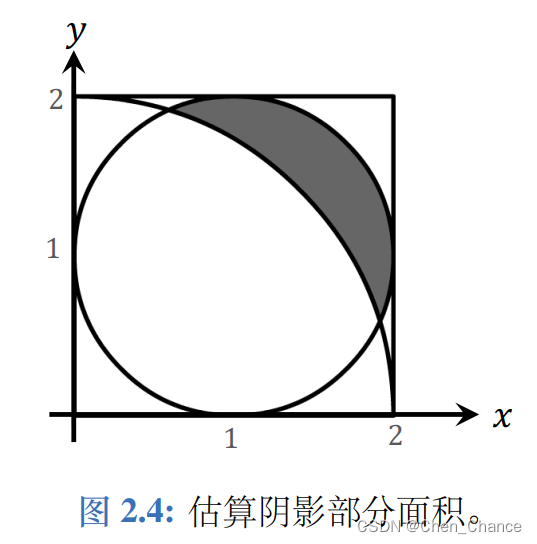
2.2.2 例二:估算阴影部分面积

2.2.3 例三:近似定积分

一元函数的定积分

多元函数的定积分

举例讲解多元函数的蒙特卡洛积分

2.2.4 例四:近似期望
蒙特卡洛还可以用来近似期望,这在整本书中会反复应用。

下面介绍一种更好的算法。既然我们知道概率密度函数 p(x),我们最好是按照 p(x)
做非均匀抽样,而不是均匀抽样。按照 p(x) 做非均匀抽样,可以比均匀抽样有更快的收敛。具体步骤如下:

注 如果按照上述方式做编程实现,需要储存函数值 f(x1), · · · , f(xn)。但用如下的方式做编程实现,可以减小内存开销。
q
n
=
1
n
∑
i
=
1
n
f
(
x
i
)
q_n=\frac{1}{n}\sum\limits_{i=1}^nf(x_i)
qn=n1i=1∑nf(xi)
初始化
q
0
=
0
q_0=0
q0=0
从
t
=
1
到
n
从t=1到n
从t=1到n
q
n
=
(
1
−
1
t
)
⋅
q
t
−
1
+
1
t
⋅
f
(
x
t
)
q_n=(1-\frac{1}{t})\cdot q_{t-1}+ \frac{1}{t} \cdot f(x_t)
qn=(1−t1)⋅qt−1+t1⋅f(xt)
2.2.5 例五:随机梯度
我们可以用蒙特卡洛近似期望来理解随机梯度算法


在这个描述中,作者提到了经验风险最小化(empirical risk minimization)问题以及在神经网络训练中使用的随机梯度下降(SGD)方法。这些方法常用于机器学习中的模型训练,特别是在深度学习中。
让我对这个描述进行进一步解释:
- 经验风险最小化问题:在机器学习中,我们通常试图训练一个模型(例如,神经网络),以便它在未见的数据上表现良好。为了实现这一目标,我们定义一个损失函数(例如,交叉熵损失),该损失函数度量模型的预测与真实标签之间的误差。经验风险最小化问题的目标是找到能够最小化在训练数据集上的损失函数的模型参数。
- 训练数据集 X:在描述中,训练数据集 X 包含 n 个样本数据点,其中每个数据点 x_i 是一个输入样本。
- 替代概率密度函数 p(x):在实际应用中,样本的真实概率密度函数 p(x) 通常是未知的,难以精确建模。因此,通常会使用一个离散的概率质量函数来代替真实的概率密度函数。在这种情况下,作者使用了一个均匀概率分布,即假设每个样本数据点被选中的概率都相等,这是一种常用的假设。
- 最小批 SGD:为了训练神经网络,通常使用随机梯度下降(SGD)的变种,例如最小批随机梯度下降。在每一轮迭代中,最小批 SGD 从训练数据集 X 中均匀随机抽取 B 个样本,其中 B 是所谓的批量大小。然后,对这些样本计算损失函数的梯度,并使用该梯度来更新神经网络的参数 w。这个过程迭代进行多次,直到满足停止条件(通常是达到一定的迭代次数或达到损失函数的收敛)。
总之,这段描述强调了在深度学习中的模型训练过程,其中采用经验风险最小化来优化模型参数,而代替真实的概率密度函数使用均匀概率分布,同时使用最小批 SGD 来提高训练效率。这是深度学习中常见的训练方法之一。