Technology-Dependent LogicOptimization, part 1

序言

如图所示是现代工业流程中对于一个高层次的抽象描述如何到最后的芯片的流程图，其中逻辑综合作为一个非常重要的部分，主要被分为两个阶段：

1. 工艺无关的优化(technology-independent optimization)

工艺无关的优化主要是通过一些抽象的cost function或者constraint对电路进行优化，例如网表的节点数、depth长度等，这篇博客里面不作详细讲解。

2. 工艺相关的优化(technology-dependent optimization)

工艺相关的优化是指利用库单元的具体的信息作为constraint进行优化，例如library cell的delay、power、area等，所有的优化都是基于具体且真实的工艺信息进行的。

本片博客的主要目的是介绍在工艺相关的优化过程中，一些常用的timing optimization方法，主要涉及ASIC芯片设计。

preliminaries (预备知识)

想要弄清楚工艺相关的优化方法，必须先学习了解有关时序分析的基础，这里会涉及到较多的公式，用心理解透了会对于timing的分析更进一步。

Gate Delay Models (delay 模型)

这里我们将会介绍三种常用的delay models，它们都是通过线性或者双线性方程来计算一个gate的pin-to-pin delay，需要注意的是，这里并没有考虑到FPGA中的Look-Up-Table based delay model.

假定给定一个gate，我们通过公式：
$$\delta (p,g)$$
定义输入 $p$ 到输出 $g$ 的delay，这也是被我们所熟知的arc delay，即工艺相关的cell的delay。

如下图所示，通过$c_g$来表示output $g$ 的累计电容，也就是我们常说的 $capacitance$($cap$)

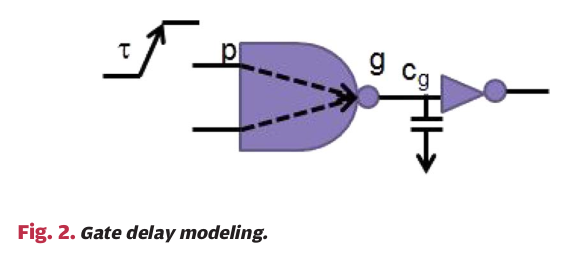
关于 $cap$ 是如何计算的，其实从前面的叙述中可以看出，$cap$ 是一个累计电容，它被定义为output $g$ 的所有扇出pin的所有input pin 的$capacitance$之和和连接到output $g$ 的所有wire load之和。

其中的 $g$ 的驱动电容被定义为：
$${\lambda }_g$$
${\lambda }_g$ 是g在不影响信号完整性或延迟规格的情况下可以驱动的最大电容。

了解了一些基本的timing相关的知识后，接下来会介绍常用的delay model，由于不同的mapper可能会选取不同的delay model，只有了解了背后的原理才能对后续的mapper有更加进一步的了解，一下delay model对于delay的计算逐渐精确。

• LIDM

首先介绍最简单的delay model是与负载无关的延时模型，即 $load-independentdelaymodel(LIDM)$，其中
$$\delta (p,g)=\alpha (p,g)$$
其中 $\alpha (p,g)$ 表示该gate固有的delay，没有考虑到任何的负载。

• LDDM

接下来介绍更加实际且使用的$load-dependentdelaymodel(LDDM)$：
$$\delta (p,g)=\alpha (p,g)+\beta (p,g)c_g$$
其中 $\beta (p,g)$ 从输入引脚p到g的电弧的负载系数，该种delay model中，不仅考虑到了改gate的固有delay，同时也考虑到了output g 的负载。

• ISDDM

最后介绍 input-slew-dependent delay model (ISDDM)，
$$\begin{gathered} \tau (h)=a(h)+b(h)c_h \\ \delta (p,g)=\alpha (p,g)+\beta (p,g)c_g+\tau (h)(k(p,g)+v(p,g)c_g) \end{gathered}$$
在这种情况下，pin-to-pin delay $\delta (p,g)$ 不仅取决于改gate的固有$delay$， 还取决于output $g$ 的负载load $c_g$ 以及 input 输入端口时钟翻转时间(slew, transition time) $\tau$。

其中，gate-dependent 系数 $\alpha$、$\beta$、a、b、k、v 通过第一次收集输入转换和输出负载值范围内的延迟和输出转换值来确定，然后在该数据上拟合上述线性和双线性形式（例如通过最小二乘法）。

determined by first gathering delay and output slew values for a range of input slew and output load values (e.g., using a circuit simulator such as SPICE) and then fitting the aforementioned linear and bilinear forms on this data (e.g., by the method of least squares).

在工业库中，ISDDM 是常用的时序模型，但是在大部分关于timing optimization的学术研究中，常用的时序模型是 LIDM 或者LDDM。

Timing analysis (时序分析)

不管使用哪一种 delay model，对于从一个电路的 primary input(PI) 或者寄存器的 $output$ 到这个电路的 primary ouput(PO) 或者寄存器的输入端的路径而言，这一条$path$的 $delay$ 等于所有的 $gate$ 的$delay$ 以及 $wire$ 的 $delay$ 之和。

整个电路的 $delay$ 等于所有这些路径中 $delay$ 最大的那一条路径。

对于 primary inputs 给定一个 arrival time A， 会通过计算这一条路径上的所有的 gate pin的arrival time得到一个forward delay;
同样的，对于 primary output，给定一个 required time，也会通过计算该条路径上每一个 gate pin的 require time得到一个backward delay，

slack of a pin/pad (a pad is a PI or aPO) 是require time和arrival time之间的差值。如果说一个pin或者pin的slack是负(negative)的，那么这条路径被称为critical的。timing优化的主要目的就是通过优化电路使得output port或者register input满足 required time的约束 (constraint)，是的电路变为non-critical。

这里有一个概念叫做 $ϵ$-criticality，一个pin/pad被称作为$ϵ$-criticality的前提是它的slack在最小的slack范围内。有一些timing optimization 算法会用来专门识别和优化$ϵ$-criticality pin/pad 。