数据结构与算法--并查集结构
- 1 岛问题
- 2 并查集结构
1 岛问题
一个矩阵中只有0和1两种值,每个位置都可以和自己的上、下、左、右 四个位置相连,如果有一片1连在一起,这个部分叫做一个岛,求一个矩阵中有多少个岛?
【举例】
001010
111010
100100
000000
这个矩阵中有三个岛
coding
package com.chao;
/**
* @author Mrchao
* @version 1.0.0
* @date 2023-10-15
*/
public class CountIslandTest {
public static void main(String[] args) {
int[][] m = {
{0, 0, 1, 0, 1, 0},
{1, 1, 1, 0, 1, 0},
{1, 0, 0, 1, 0, 0},
{0, 0, 0, 0, 0, 0}
};
System.out.println(countIsland(m));
}
public static int countIsland(int[][] m) {
if (m == null || m[0] == null) {
return 0;
}
int M = m.length;//行数
int N = m[0].length;//列数
int ret = 0;
/**
* 遍历一遍岛屿 碰到 1 则进行一次感染过程
*/
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
if (m[i][j] == 1) {
ret++;
infect(m, i, j, M, N);
}
}
}
return ret;
}
/**
* 二维数组 m 中与 m[i][j]直接相邻 或间接相邻的点 全部修改为 2
*
* @param m
* @param i
* @param j
* @param M 二维数组行数
* @param N 二维数组的列数
*/
public static void infect(int[][] m, int i, int j, int M, int N) {
if (i < 0 || i >= M || j < 0 || j >= N || m[i][j] != 1) {
return;
}
m[i][j] = 2;
infect(m, i - 1, j, M, N);
infect(m, i + 1, j, M, N);
infect(m, i, j - 1, M, N);
infect(m, i, j + 1, M, N);
}
}
时间复杂度 O ( M ∗ N ) O(M * N) O(M∗N)
2 并查集结构
并查集对外提供的操作 :
-
集合的合并 合并两个集合 形成一个更大的集合
-
集合的查询 判断两个元素是否在同一个集合中
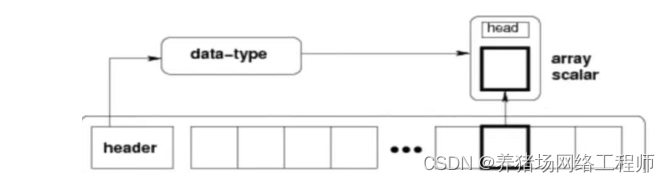
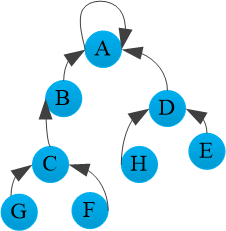
如图所示
public class UnionFindTest {
// 并查集中的元素
public static class Element<V> {
public V value;
public Element(V value) {
this.value = value;
}
}
public static class UnionFindSet<V> {
public Map<V, Element<V>> elementMap;// key 某个具体的值 value key 对应的元素
public Map<Element<V>, Element<V>> fatherMap;// key 并查集中的某个元素 value : 该元素的父 当前元素向上指的元素
public Map<Element<V>, Integer> sizeMap;// key 代表元素 value 该集合中元素的个数
public UnionFindSet(List<V> list) {
elementMap = new HashMap<>();
fatherMap = new HashMap<>();
sizeMap = new HashMap<>();
for (V v : list) {
Element<V> element = new Element<>(v);// 创建元素
elementMap.put(v, element);
fatherMap.put(element, element); // 当前每个节点的父都是自己
sizeMap.put(element, 1); // 每个集合中的元素的个数都是 1
}
}
/**
* 给定一个元素一直往上找 把代表元素返回
*
* @param e
* @return
*/
private Element<V> findHead(Element<V> e) {
Stack<Element<V>> path = new Stack<>();
// 没有找到父 就一直找
while (e != fatherMap.get(e)) {
path.push(e);
e = fatherMap.get(e);
}
// 到此找到了 父元素
// 把沿途遍历过的所有的元素都挂在当前的父元素上
while (!path.isEmpty()) {
fatherMap.remove(path.pop(), e);
}
return e;
}
/**
* 判断 两个值是否在同一个集合中
*
* @param v1
* @param v2
* @return
*/
public boolean isSameSet(V v1, V v2) {
if (elementMap.containsKey(v1) && elementMap.containsKey(v2)) { // v1 v2 初始化过
return findHead(elementMap.get(v1)) == findHead(elementMap.get(v2));
}
return false;
}
/**
* 将两个值合并为一个集合
*
* @param v1
* @param v2
*/
public void union(V v1, V v2) {
if (elementMap.containsKey(v1) && elementMap.containsKey(v2)) { // 被初始化过
Element<V> fHead = findHead(elementMap.get(v1));
Element<V> sHead = findHead(elementMap.get(v2));
if (fHead != sHead) { // 不在同一个集合中 才进行合并
// 数据较少的集合的顶端挂在数据较多的数据的顶端的底下
Element<V> big = sizeMap.get(fHead) >= sizeMap.get(sHead) ? fHead : sHead;
Element<V> small = big == fHead ? sHead : fHead;
fatherMap.put(small, big);
sizeMap.put(big, sizeMap.get(fHead) + sizeMap.get(sHead));
sizeMap.remove(small);
}
}
}
}
}