《图》
- 图的存储(顶点和边)
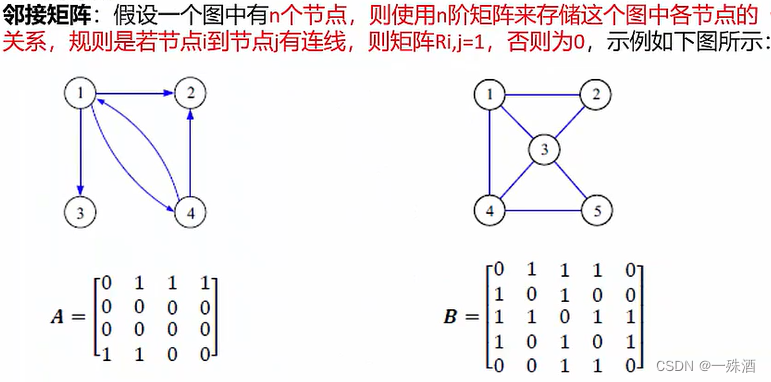
- 邻接矩阵:适合边数较多的图,不易造成浪费
- 无向图:不分方向;对称矩阵
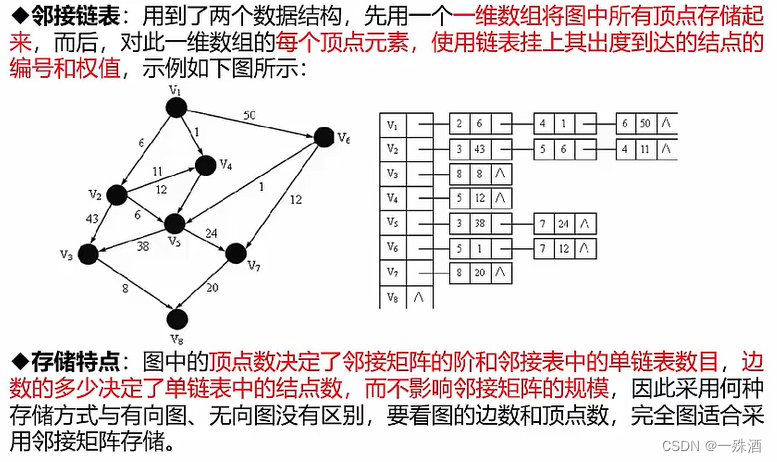
- 邻接链表:顶点,边——>(编号,权值);无值为空“∧”
- 邻接链表顶点的表结点 ——> 出度
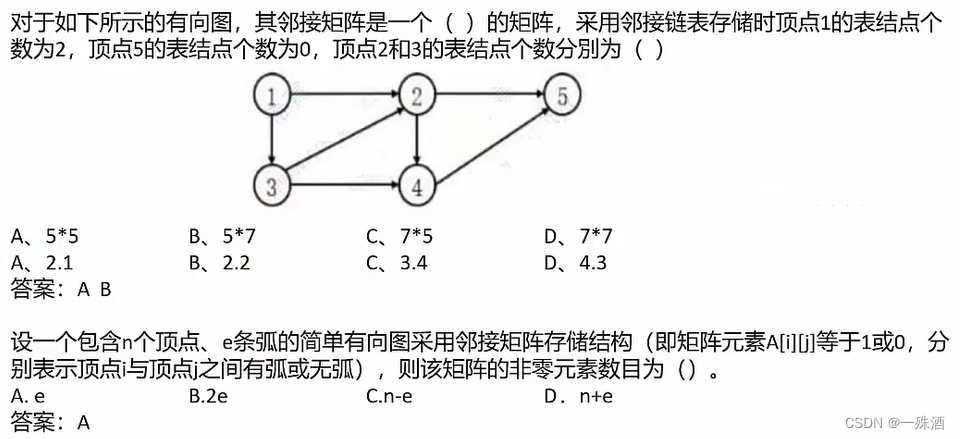
- A[ i ] [ j ] 等于1或0 ——> i 和 j 之间存在弧
- e 条弧,有向图则有 e 个非零元素(i ——> j),无向图则有 2e 个(i ——> j;j ——> i)
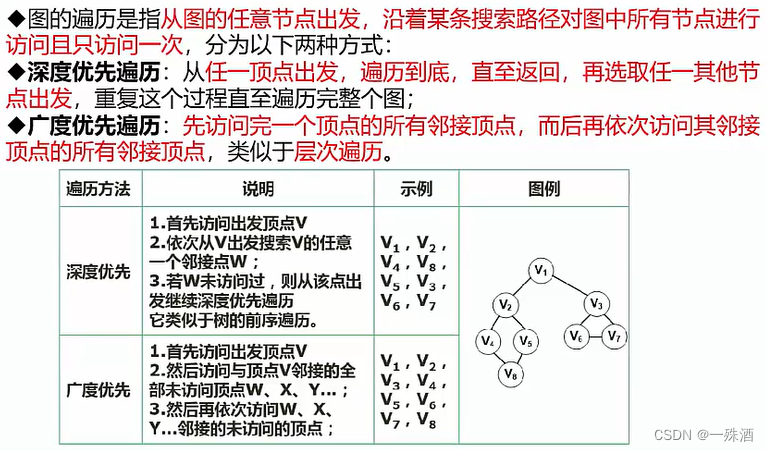
- 图的遍历
- 图的遍历序列不唯一,树的遍历序列唯一
- 深度优先遍历:某一顶点出发,遍历到底(下层),再返回
- 广度优先遍历:某一顶点出发,访问所有邻接顶点(同层),遍历到底——>层次遍历
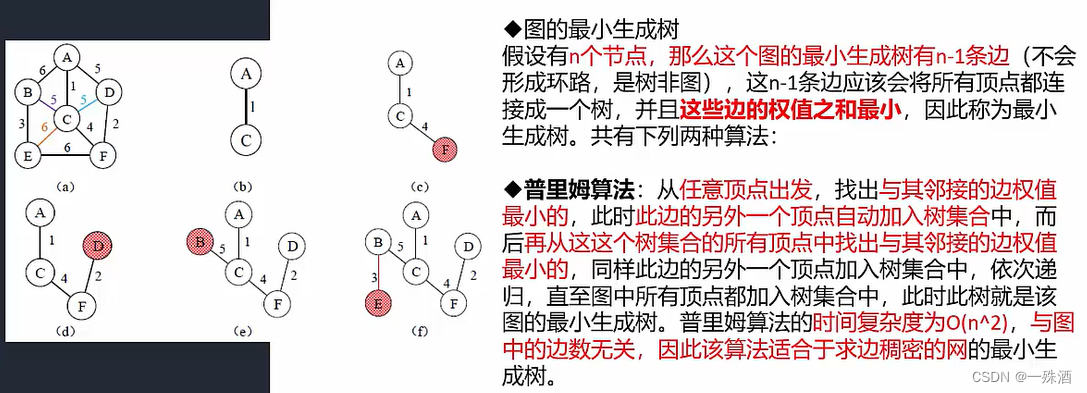
- 图的最小生成树
- n个节点,图的最小生成树有 n -1 条边,不能形成环——>形成树,边的权值之和最小
- 普里姆算法:
- 从顶点出发,依次寻找权值最小的邻接边
- 时间复杂度为O(n^2)
- 与图的边数无关;适用于边稠密的最小生成树
- A(1,5,6)——> AC(4,5,6)——> ACF(2,5,6)——> ACFD()——> ACFD B(3,6)——> ACFDB E()
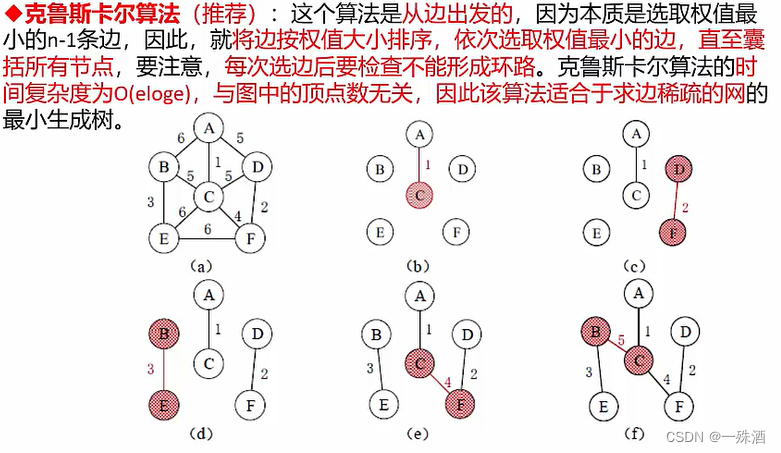
- 克里斯卡尔算法:
- 从边出发,依次寻找权值最小的邻接边
- 时间复杂度为O(eloge)
- 与图的顶点数无关;适用于边稀疏的网的最小生成树
- AC(1)——> DF(2)——> BE(3)——> CF(4)——> BC(5)
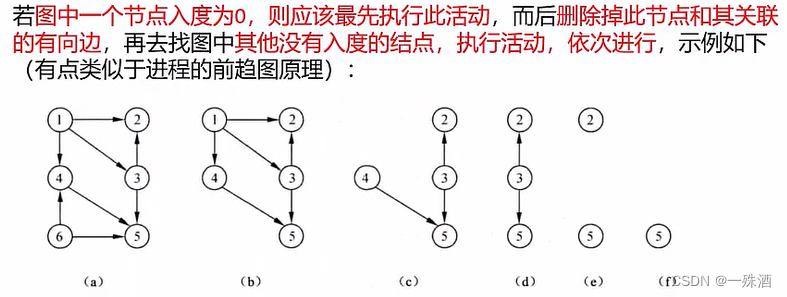
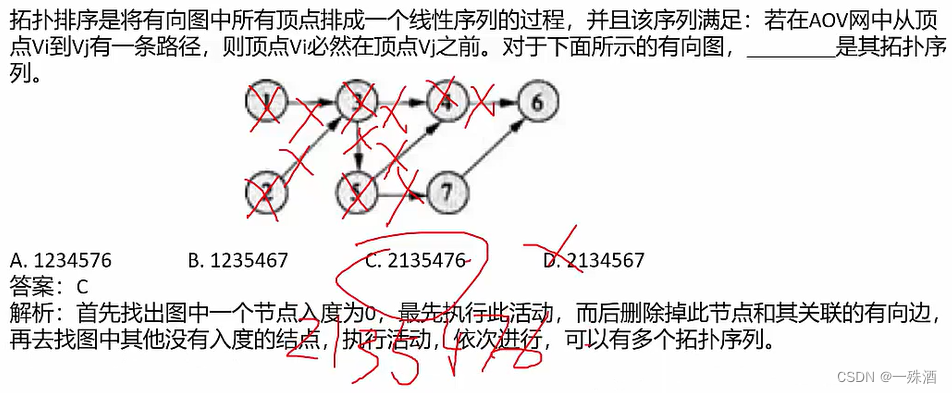
- 拓扑序列
- 找到在图里面按照顺序执行的序列,不依赖于其他事务;类似进程的前趋图原理
- 删除入度为0的节点及与其相关的有向边
- 序列不唯一
《顺序查找》
- 从头到尾查找,符合返回,否则失败
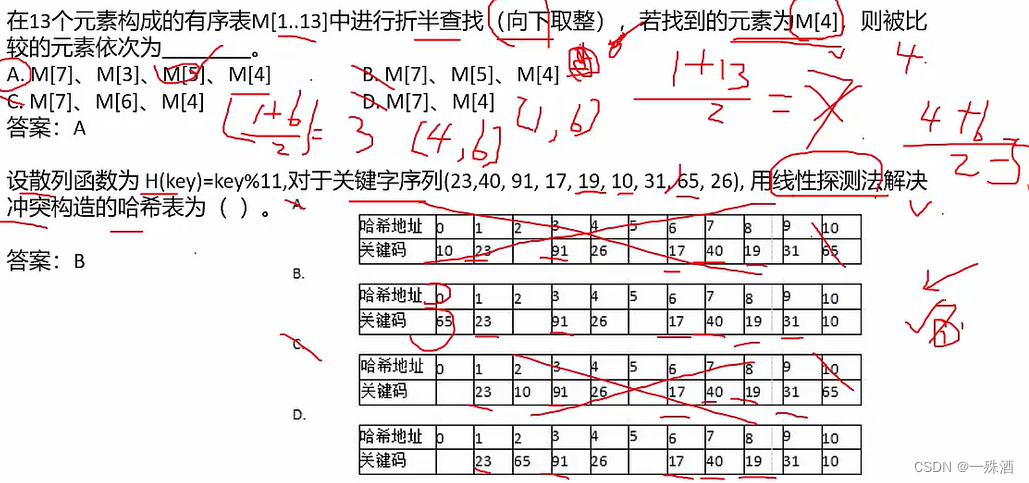
《折半查找》
- 只适用于待查找序列中的元素是有序排序的情况
- 每次查找取中间值,舍弃上次中间值序列
- 中间值为小数时,要向下取整
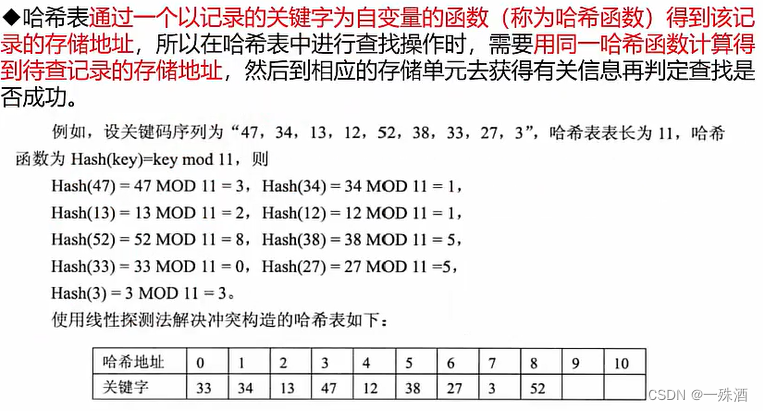
《哈希表》
- Hash(key)= key mod 表长
- 一个地址只能存储一个记录
- 哈希函数产生冲突解决方法
- 多个关键字执行同一个哈希函数时,产生相同的地址/结果,则产生了冲突
- 线性探测法:执行后取得的地址依次+1,直到可存储到尚未存储关键字的哈希地址中;
- 只有 [ 0,10 ],没有11,则形成了一个环,则 65 的哈希地址 10 + 1 ——> 0