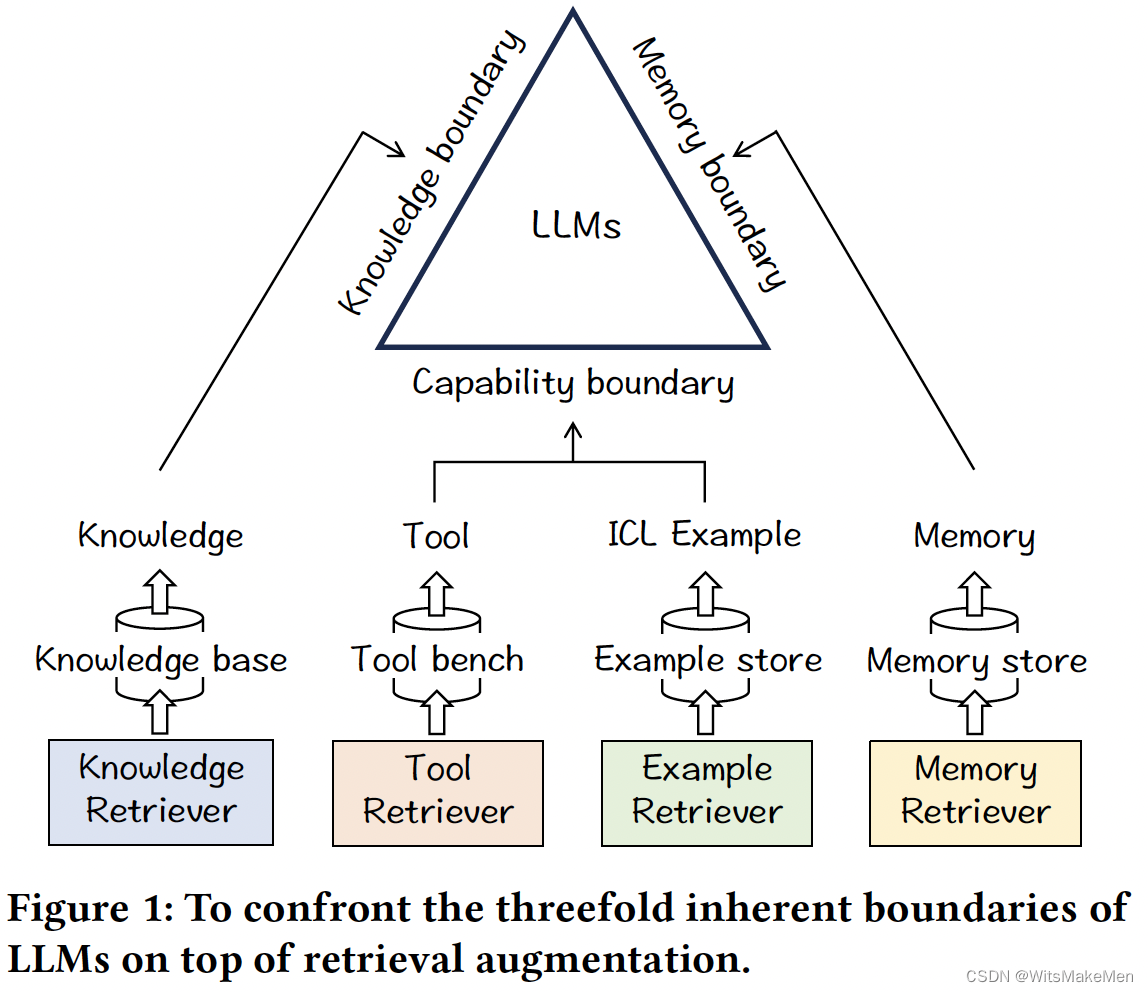
文章目录
- 线性回归回顾
- 逻辑回归

Hi,你好。我是茶桁。
上一节课,在结尾的时候咱们预约了这节课一开始对上一节课的内容进行一个回顾,并且预告了这节课内容主要是「逻辑回归」,那我们现在就开始吧。
线性回归回顾
在上一节课中,我们定义了model,loss函数以及求导函数。最后我们用for循环来完成了求导过程。本节课一开始,咱们先来对上一节课的代码做一次优化,优化后的代码也会上传到课程代码仓库内。
此部分代码依然在08.ipynb中。
首先,我们将之前的model重新更名为linear, 以便知道我们这个函数是要做什么的。接着,我们把for循环内对w和b的偏导封装为一个函数,便于我们之后调用:
def optimize(w, b, x, y, yhat, pw, pb, learning_rate):
w = w + -1 * pw(x, y, yhat) * learning_rate
b = b + -1 * pb(x, y, yhat) * learning_rate
return w, b
然后我们将整个for循环封装一下:
def train(model_to_be_train, target, loss, pw, pb):
w = np.random.random_sample(size = (1, 2))# w normal
b = np.random.random()
learning_rate = 1e-5
epoch = 200
for i in range(epoch):
for batch in range(len(rm)):
# batch trainning
index = random.choice(range(len(rm)))
rm_x, lstat_x = rm[index], lstat[index]
x = np.array([rm_x, lstat_x])
y = target[index]
yhat = model_to_be_train(x, w, b)
loss_v = loss(yhat, y)
batch_loss.append(loss_v)
w, b = optimize(w, b, x, y, yhat, pw, pb, learning_rate)
if batch % 100 == 0:
print('Epoch: {} Batch: {}, loss: {}'.format(i, batch, loss_v))
return model_to_be_train, w, b
在最后呢,我们可以在调用函数之前,导入所需第三方库,然后将之前的数据处理在执行函数前获取并处理一遍:
import matplotlib.pyplot as plt
import random
import pandas as pd
import numpy as np
from sklearn.datasets import fetch_openml
dataset = fetch_openml(name='boston', version=1, as_frame=True, return_X_y=False, parser='pandas')
data = dataset['data']
target = dataset['target']
columns = dataset['feature_names']
dataframe = pd.DataFrame(data)
dataframe['price'] = target
rm = dataframe['RM']
lstat = dataframe['LSTAT']
model, w, b = train(linear, target, loss, partial_w, partial_b)
为什么我们每次都要随机取一个数字呢?
你也可以把所有的x全部输入进去,所有的y全部输入进去。但是实际上在整个场景下,比方说我们有很多的训练数据,每个训练数据都有一个x,有一个y。
loss函数本来写的是i属于所有的N,y_i减去yhat_i的平方。但是现在如果把所有的x和所有的y在真实的场景下输入进去的话,假设现在x有100万个或者200万个,输入进去之后整个求解过程可能loss函数这个程序加载都加载不出来,会非常非常慢。
所以在实际的工作中,假如说i属于D: ∑ i ∈ D \sum_{i \in D} ∑i∈D,D就是distribution的意思,就是随机取一些数据,然后再把随机取的一些数据求解。这样的话每一次就可以保证它可以运行。
但是这样的一个区别是什么?
每次把所有的x和y都输入进去,这种梯度下降方式中loss下降是一个很顺滑的样子,这个叫做BGD。
还有一种情况就是咱们课上用的这种剃度下降方式,每次随机取了一个随机值,叫随机剃度下降,就随机取一个数字做梯度下降,简称SGD。这个loss下降就会上下波动很厉害。如我们上面展示的图。
再下来呢还有一种,它是取这两者之间,每次不是取一个,是取了多个。我们把这个叫做MBGD。
这是三种梯度下降方式。在实际的工作中SGD用的最多,因为可以快速的进行梯度下降学习。
我们可以将代码修改一下:
batch_size = 10
for i in range(epoch):
...
for batch in range(len(rm) // batch_size):
indices = np.random.choice(range(len(rm)))
rm_x, lstat_x = rm[indices], lstat[indices]
x = np.array([rm_x, lstat_x])
y = target[indices]
...
关于这一部分内容,这里仅仅是提一下,在后面的课程中,我们还会更详细的来讲解。
我们在循环中,将原来的次数50替换成了epoch, epoch在机械学习里边指的是运行了整整一遍。
在第二个循环内,里面是rm个东西,每次都是随机取,我们随机取了多少次呢?取了rm个。也就是说平均每个样本会被取样一次。
这就是数据量大的好处,当数据量很大的时候,有个别的点没有取到或者说有个别的点取了多次其实对最终的效果是不影响的。
也就是说因为数量很大,所以一两次的变化,一两个数值取的少了或者取的多了,其实不是非常影响。
我们把每次epoch的batch打出来,我们来看一下:
def train(...):
...
losses = []
for i in range(epoch):
batch_loss = []
for batch in range(len(rm)):
...
batch_loss.append(loss_v)
...
losses.append(np.mean(batch_loss))
return model_to_be_train, w, b, losses
model, w, b, losses = train(linear, target, loss, partial_w, partial_b)
plt.plot(losses)
plt.show()
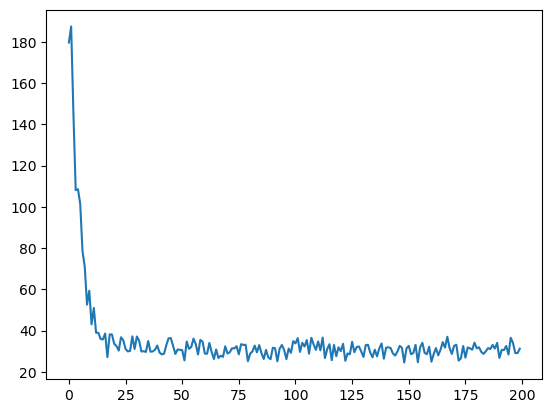
那如果是上面我们更改的代码,使用了batch_size控制之后,图形就完全不一样。
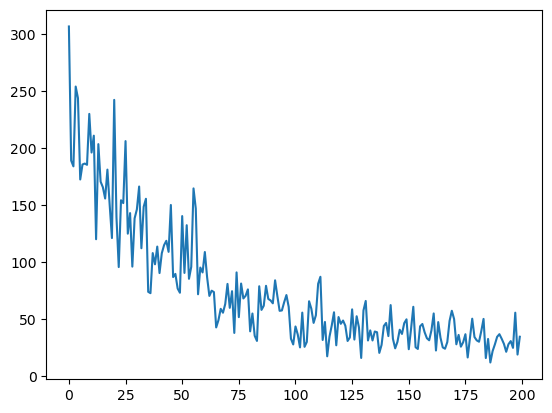
可以看到,这个loss下降还是挺明显的。
这个时候,我们假设知道一组的rm等于19,lstat等于7。而此时其实已经有了w和b,求到最终的w和b,就能够有一个预测值了。
predicate = model(np.array([19, 7]), w, b)
print(predicate)
---
Epoch: 0 Batch: 0, loss: 46.17245060319155
...
Epoch: 199 Batch: 0, loss: 0.2053457975383563
我们在这个实例中,只用了两个最显著的特征,如果把x的维度变多一些,其实就会更加接近了。
好,这个线性回归的过程,其中包括线性函数的定义,为什么要用线性函数,loss函数的意义,梯度下降的意义就都讲完了。
这个内容是我从斯坦福大学的参考书上弄过来的。
除了定义一个这样一个平方值的loss,可以定一个绝对值loss,都是一样的,都可以实现找到最优值。
只不过这个二次方的这个loss对于结果, 它的惩罚会更大一些。
经过这一段代码的洗礼,对于之前的那个数学式子应该能看的更明白一些了。
逻辑回归
我们讲完了线性回归,下面再跟大家来讲一下逻辑回归。
逻辑回归是什么?假如还是如上那个问题,前面代码都没变。当然,库需要再导入一遍:
import random
import pandas as pd
import numpy as np
from sklearn.datasets import fetch_openml
dataset = fetch_openml(name='boston', version=1, as_frame=True, return_X_y=False, parser='pandas')
现在咱们要变一个问题场景, 我们先打印一下np.percentile(), 这是要求百分位,比方说我们填入一下target, 其实我们数据预处理的时候知道,就是dataframe['price']:
print(np.percentile(target, 66))
我们写入一个target, 其实就是price,然后我们在后面写了一个66,也就是说,我们将这里所有的price,也就是房价,做了一次排序,然后,我取从0到100中的第66%个位置的数值, 就是大于2/3的房价。同样的,如果我这里填了一个50,那么就是取最中间的那个值。
输出的结果为23.53, 是23万美金。还是比较便宜,23万美金折合100多万。
好,现在我们来做一个判断:
greater_then_most = np.percentile(target, 66)
dataframe['expensive'] = dataframe['price'].apply(lambda p: int(p > greater_then_most))
print(dataframe[:20])
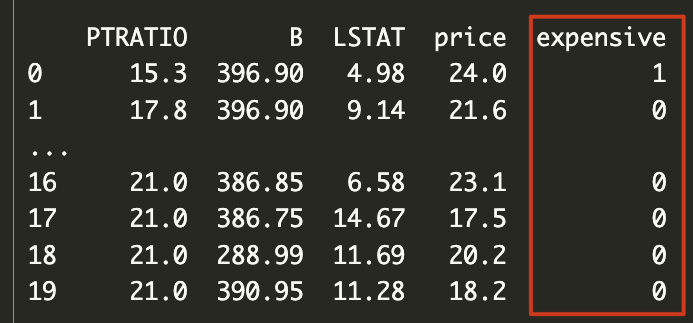
我们定义了一个expensive, 在dataframe中加入了这个特征。这个特征在房价大于2/3房价的时候int为1, 否则为0。
做了这样一件事之后,就是问这个房子是不是贵房子,如果是1,就是贵房子,0就不是贵房子。根据我们添加的特征来进行判断。
那接着呢,问题发生了改变。我们不知道这个房子的price, 现在需要进行预测这个房子是不是属于一个高档小区。在预测中,假如是1, 就表示是高档小区,0就表示不是高档小区。现在要根据它的一些特征来猜测它是不是高档小区。
我们刚刚其实已经知道,所谓的高档小区其实是和价格有一定关系的。
假如说现在咱们有一个问题要求解,现在要有一个模型能够预测它到底是1还是0,或者我们要预测是开心还是难过,咱们现在只要做一件事情就可以,就是把我们期望目标标成1, 把另外那个相对的目标标成0。
如果我们能够拟合一个函数,这个函数的输出要么是1,要么是0,我们让这个模型的值越接近于实际的值就可以了。

比方说刚刚回顾完的线性回归,给定的(x, y)里边,y这个值它是一个实数。如果现在变成了0、1。比方说1就是happy,0就是sad。或者还是用咱们之前定义的:1就是expensive,0就是not expensive。
把1和0认为是概率,如果是概率的话,1就是100%是,0就100%不是。
那么咱们之前的model输出的是实数\in R, 这次需要的model就是输出的是0~1。这个模型的任务就变成了如果x给定的是1,那么model输出最后要尽可能的接近1。
怎么样才能让我们的model输出是0到1之间呢?有一个方法,一个函数叫做logistic函数, logistic function:
J
(
θ
)
=
−
∑
i
(
y
(
i
)
l
o
g
(
h
θ
(
x
(
i
)
)
)
+
(
1
−
y
(
i
)
)
l
o
g
(
1
−
h
θ
(
x
(
i
)
)
)
)
\begin{align*} J(\theta)=-\sum_i(y^{(i)}log(h_{\theta}(x^{(i)}))+(1-y^{(i)})log(1-h_{\theta}(x^{(i)}))) \end{align*}
J(θ)=−i∑(y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i))))
这个函数其实在复杂系统里面是一个很重要的函数, 人们其实是期望获得一种导数,数学家们研究的是这个:y’ = y(1-y), 就是y的导数等于y乘以1-y。研究完了之后发现有一种函数就满足这个特征:
f
(
x
)
=
1
1
+
e
−
x
\begin{align*} f(x) = \frac{1}{1+e^{-x}} \end{align*}
f(x)=1+e−x1
这个函数的值画出来,就是这个样子:
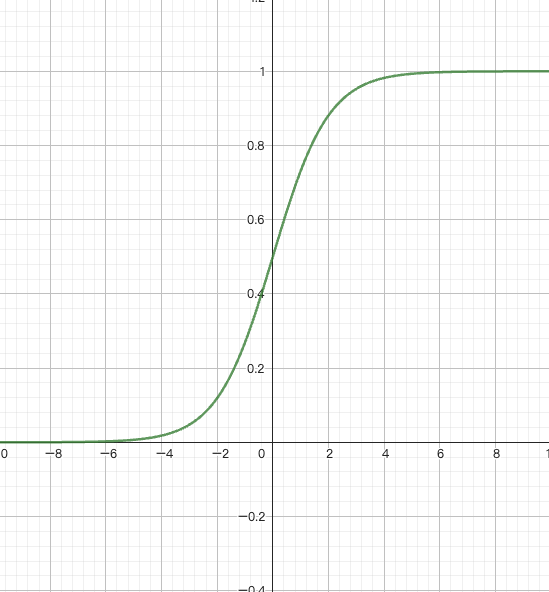
值全部是从0到1之间,中间与y轴交点为0.5。
给大家讲一下这个原理,逻辑函数原本是想研究y’=y(1-y),求解出来有这样一个函数满足这样的特征:f(x) = 1/1+e^{-x}。那我们这里需要注意一下,这个特征以后会有大用。把它的图形画出来呢,就是如上图这样的一种函数, 这个函数值就是在0~1之间。
为什么我们要用逻辑函数来做概率预测呢?首先第一个原因就是因为它的值本身输出就是0~1之间,天然的适合做概率这块,第二,他还处处可导, 逻辑函数它是处处可导的。
所以我们就可以用这个函数来进行分类,可以把原来的模型f(x)=wx+b, 这整个模型写成:
f
(
x
)
=
1
1
+
e
−
(
w
x
+
b
)
\begin{align*} f(x) = \frac{1}{1+e^{-(wx+b)}} \end{align*}
f(x)=1+e−(wx+b)1
原来的f(x)拟合的是等于wx+b, 现在把这个f(x)变成如上式的样子。这个输出的就变成0-1了,就能够让它的值在0到1之间变换。
这就是为什么我们把这种方法叫做逻辑回归的原因。就是它是在回归曲线上加了一个逻辑函数,所以我们称其为逻辑回归。
加上逻辑函数虽然输出的值是0~1之间,但其实是在做分类。越接近于1就越近于一类,越近于0就越近于另一类。逻辑回归本质上就是在做分类。
接着,咱们来上代码给大家详细的讲解一遍。
其实我们整个代码和之前实现的线性回归非常的像,唯一的区别是我们需要一个叫做sigmoid的函数,也就是逻辑函数。
def sigmoid(x):
return 1/(1+np.exp(-x))
我们来把这个函数画出来看看是什么样的:
plt.plot(sigmoid(np.linspace(-10, 10)))
plt.show()
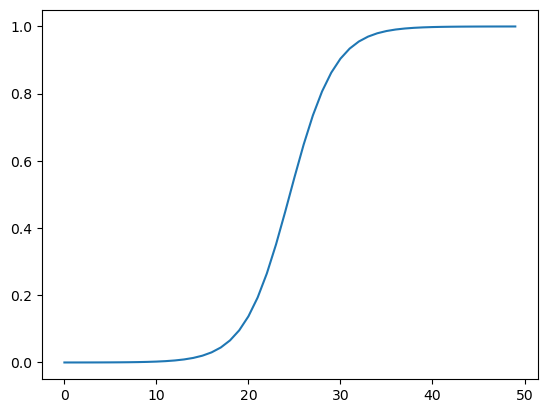
其实, 机器学习是个很简单的问题。机器学习其实是计算机里面最简单的几个部分,哪些比这更复杂呢?第一个、编译器原理,还有程序设计语言与自动机,还有计算机图形学,复杂系统,还有计算复杂性,操作系统。其实这些都比
深度学习复杂的多。
为什么我们现在深度学习用的多,就是因为深度学习简单。所以我说这些题外话是想告诉大家,在学习这个的时候不要有什么顾虑和负担,放松一点,放开膀子撸起袖子干就完了。
好,我们现在把model写出来:
def model(x, w, b):
return sigmoid(np.dot(x, w.T) + b)
那么来看, 我们现在如果要预测, 给一个rm和lstat输入进去, 一个RM和LSTAT的值输入进去。
我们先来看一下真实的值是怎样的:
rm = dataframe['RM']
lstat = dataframe['LSTAT']
target = dataframe['expensive']
epoch = 200
for i in range(epoch):
for b in range(len(rm)):
index = random.choice(range(len(rm)))
x = np.array([rm[index], lstat[index]])
y = target[index]
print(x, y)
这个呢就是我们在训练时候每个给的数据,每次给他给一组数据,然后给它的这个值到底是0还是1。 我们期望的是求解一组(w,b),能够让它输入x的时候也能得到0或者1。就它真实的时候是0,期望的是这一组输入进去之后,根据(w,b)运行完了之后也是0。这个就是我们的目标。
假如已经获得线性回归了,然后要通过线性回归加一些东西想实现0和1的分类。之前我们在线性回归那里是不是先定义了一个loss函数?把loss函数定义清楚之后再对loss求偏导就可以了。那这里也是一样,需要定义loss,只要把loss定义出来之后给loss求偏导就可以了,和之前一模一样。
现在的问题就转变成,咱们怎么求loss呢?
我们的目标给定如果是0那么yhat也要是0。y是1的时候yhat也得是1。如果y等于1的情况下,yhat等于0,就意味着错的很厉害啊。相对的,y等于1,yhat等于0也同样是错的很厉害。
那么,如果y等于1的时候,yhat等于0.9, 错的就比较少。yhat等于1的时候,错误就是0,也就是没错误。
那么我们就可以写-log(yhat), 把这个写出来就是这样一个函数:当它越接近于0的时候,loss值会接近于无穷大, 当它接近于1的时候, loss会接近于0。
当y等于1的时候,loss可以等于-log(yhat)。如果y等于0,lose值就越接近于无穷大。这个时候loss就可以写成-log(1-yhat)。
那么现在这里就出现一个问题,也是通常面试时候的一个高频题:为什么在逻辑回归里,loss函数不直接写成1-yhat?
就是,如果y等于1的情况下,loss函数不直接写成1-y, 当y等于0的时候,loss不直接写成y。
因为这样会导致这条线呈现出一个直线,所有的偏导结果都是一致没有发生变化。
就好比有一个孩子考试成绩特别差,假如现在的目标是等于1,他的成绩特别特别差,0.001。现在的这个梯度还是比较小,他考特别好的时候这个梯度还是一样。
但是我们知道,梯度代表了接下来的变化方向和力度。这个就是我们为什么要用这个的原因。
当然,其实还有一些概率上的解释,这里就不继续延展着讲了。
对于上面讲的,当y=1和y=0的两个不同的loss函数,可以做一个归纳,写成一个loss函数:
l o s s = − ( y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ) loss = - (ylog\hat y + (1-y) log(1-\hat y)) loss=−(ylogy^+(1−y)log(1−y^))
为什么能够变成这样呢?我们来分析一下,如果y=0的时候,那ylog(yhat)就等于0,也就是说仅剩下(1-y)log(1-yhat), 反过来,当y=1的时候,等式后面部分就等于0,仅剩下ylog(yhat)。
那下面,我们就来完成代码来实现:
def loss(yhat, y):
return -np.sum(y*np.log(yhat) + (1-y)*np.log(1-yhat))
lose函数求解出来之后,对于(w,b)怎么求偏导呢?
那么其实式子就可以变成:
−
(
y
l
o
g
σ
(
w
x
+
b
)
+
(
1
−
y
)
l
o
g
σ
(
1
−
(
w
x
+
b
)
)
)
−
(
y
l
o
g
σ
(
w
1
x
1
+
w
2
x
2
+
b
)
+
(
1
−
y
)
l
o
g
σ
(
1
−
(
w
1
x
1
+
w
2
x
2
+
b
)
)
)
\begin{align*} & -(ylog \sigma (wx+b) + (1-y)log \sigma (1-(wx+b))) \\ & -(ylog \sigma (w_1x_1+w_2x_2+b) + (1-y)log \sigma (1-(w_1x_1+w_2x_2+b))) \end{align*}
−(ylogσ(wx+b)+(1−y)logσ(1−(wx+b)))−(ylogσ(w1x1+w2x2+b)+(1−y)logσ(1−(w1x1+w2x2+b)))
那么对其求偏导, 一系列推导完成后就可以变成:
∂
l
o
s
s
∂
w
i
=
∑
(
y
^
−
y
)
x
i
\begin{align*} \frac{\partial loss}{\partial w_i} & = \sum(\hat y - y) x_i \end{align*}
∂wi∂loss=∑(y^−y)xi
我们来完成其函数代码,和线性部分一样,包含对w和b求导两部分:
def partial_w(x, y, yhat):
return np.array([np.sum((yhat-y) * x[0]), np.sum((yhat-y) * x[1])])
def partial_b(x, y, yhat):
return np.sum((yhat - y))
那接下来我们干嘛?上节课的内容还有印象吗?接下来我们要给w,b随机值对吧?
w = w = np.random.random_sample((1,2))
b = np.random.random()
接着我们修改上面实现过的对真实值的实现代码, 删掉我们曾经打印的(x,y),然后利用我们实现的loss函数和偏导函数来计算预测值。
rm = dataframe['RM']
lstat = dataframe['LSTAT']
target = dataframe['expensive']
learning_rate = 1e-5
epoch = 200
losses = []
for i in range(epoch):
batch_loss = []
for batch in range(len(rm)):
index = random.choice(range(len(rm)))
x = np.array([rm[index], lstat[index]])
y = target[index]
# print(x, y)
yhat = model(x, w, b)
loss_v = loss(yhat, y)
w = w + -1 * partial_w(x, y, yhat) * learning_rate
b = b + -1 * partial_b(x, y, yhat) * learning_rate
if batch % 100 == 0:
print('Epoch: {}, Batch: {}, loss:{}'.format(i, batch, loss_v))
losses.append(np.mean(batch_loss))
执行完之后,我们可以看到loss在慢慢的变小。
现在我们在数据中随机取一些数据,比如说我们去100个吧,用于去预测,检验我们的模型:
random_test_indices = np.random.choice(range(len(rm)), size=100)
for i in random_test_indices:
print('RM:{}, STAT:{}, TARGET:{}, PRE:{}'.format(rm[i], lstat[i], target[i], model(np.array([rm[i], lstat[i]]), w, b)))
---
RM:6.425, STAT:12.03, TARGET:0, PRE:[0.15662289]
...
RM:5.0, STAT:31.99, TARGET:0, PRE:[4.87033539e-06]
...
RM:8.247, STAT:3.95, TARGET:1, PRE:[0.9623407]
...
RM:7.686, STAT:3.92, TARGET:1, PRE:[0.95077171]
我随机展示了一些数据,我们从这里能看到,预测值内有的值偏向0,有的值甚至比1还要大。对比前面的TARGET真实值来看,预测的大部分还是准确的。
不过这个时候还是有问题,我们做这个预测的初衷是为了要做分类,也就是到底是0还是1,那PRE值到底是什么,怎么分类呢?咱们就要牵扯到一个东西:dicision boundary。
也就是决策的边界,咱们假定为0.5,让我们拿到的预测值去和这个边界值做对比,大于它的就是1,小于的就是0:
dicision_boundary = 0.5
predicate_label = int(predicate > decision_boundary)
有了这个之后,我们需要更改下我们之前的代码:
random_test_indices = np.random.choice(range(len(rm)), size=100)
decision_boundary = 0.5
for i in random_test_indices:
x1, x2, y = rm[i], lstat[i], target[i]
predicate = model(np.array([x1, x2]), w, b)
predicate_label = int(predicate > decision_boundary)
print('RM:{}, LSTAT:{}, EXPENSIVE:{}, Predicated:{}'.format(x1, x2, y, predicate_label))
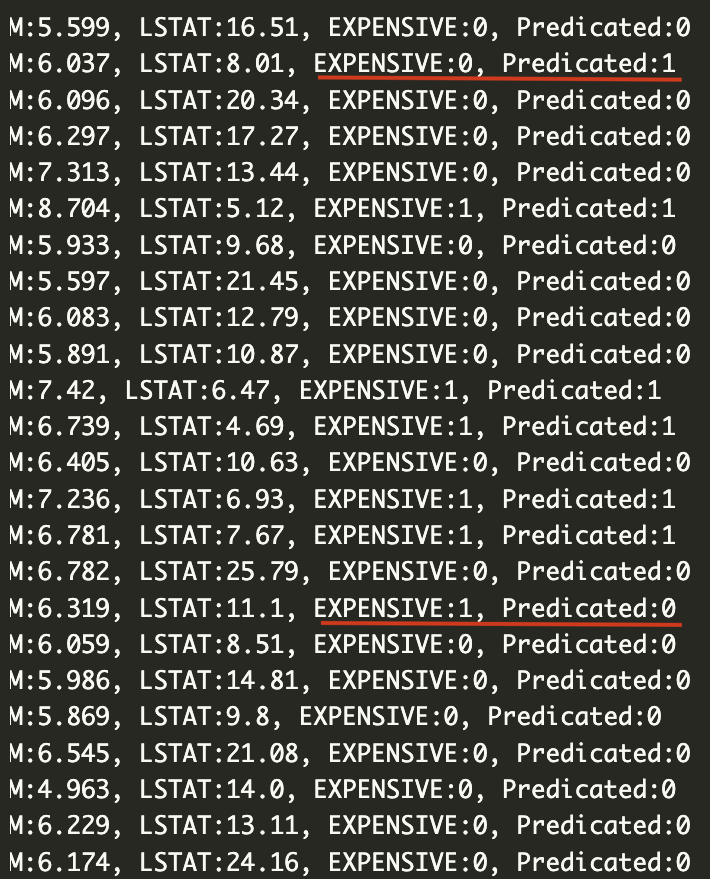
更改完之后我们执行,和真实值进行对比,我们发现整个预测的还算事准确。当然也有部分预测错误的。
现在这个模型能够预测出来了,根据两个值能够预测出来它到底属于一个高档房子,还是不属于一个高档房子。但是我们会发现其实还有算错的地方。那么现在要问,如何衡量模型的好坏?以下就是我们要继续研究的问题:
- accuracy 准确度
- precision 精确度
- recall 召回率
- f1, f2 score
- AUC-ROC 曲线
这些就是我们用于衡量模型的一些指标,通过这个,我们要引出一个非常重要的概念,就是过拟合和欠拟合(over-fitting and under-fitting)。我们可以说,整个机器学习的过程,就是在不断的进行过拟合和欠拟合的调整。那么这些呢,就是我们下面课程的内容了。
目前来讲,我们学习了监督学习里面最重要的线性回归和逻辑回归,接下来什么我们要去学的LSTM,CNN等等,其实都是为了提高这个准确度所要做的事情。
也就是,现在我们发现虽然模型还是稍微有一些错误,这个时候就需要一起来再研究一下如何衡量模型的好坏。只有知道了如何衡量模型的好坏,才知道怎么样去调整它,怎么去优化它。
好,那下节课记得不见不散。