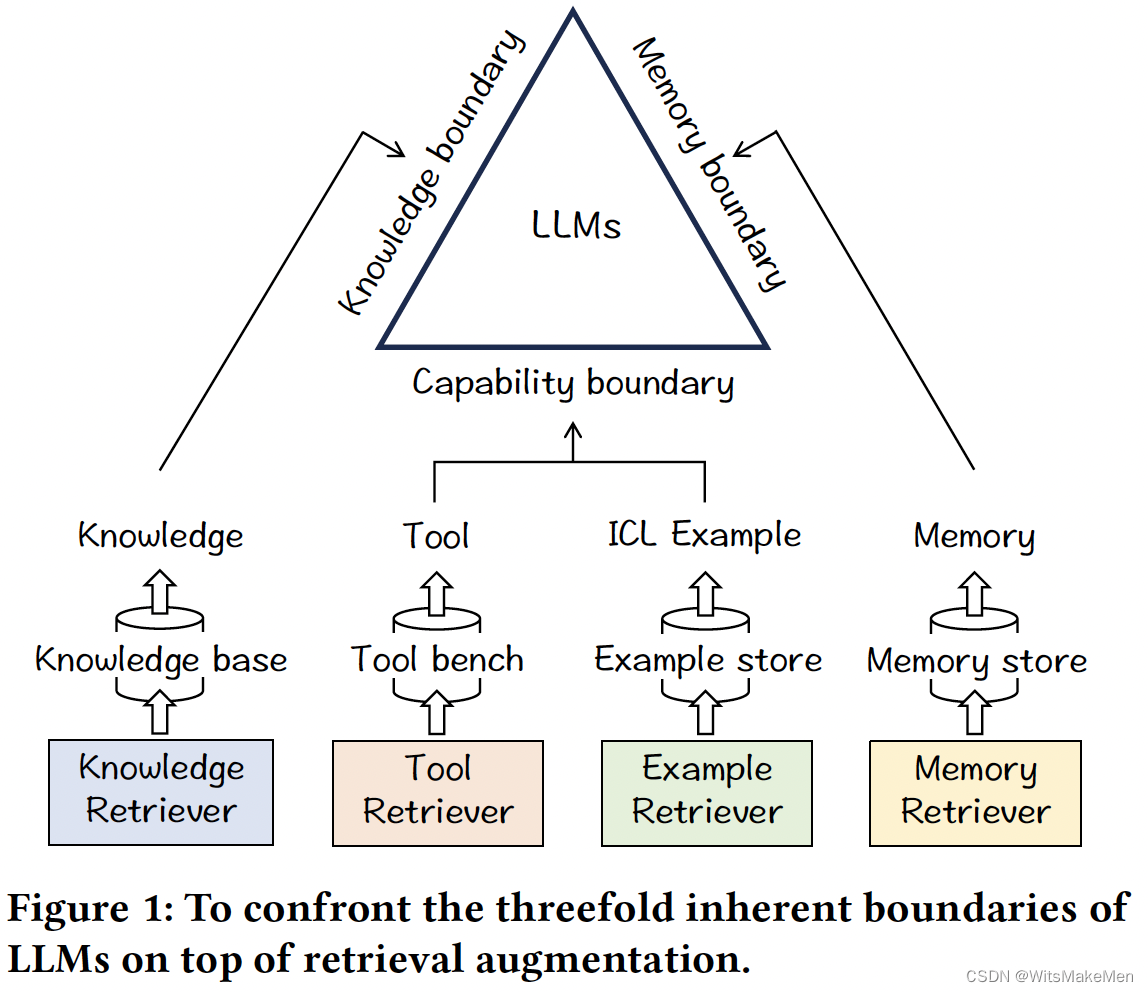
有种走法，因为需要向上走m步，向右走n步。

显然分子分母分别算出，再相除不太可能，那么分别求出分子和分母的质因子相乘的形式。分子存入up数组中，分母存入down数组中，数组中的元素对应之差final_数组即代表分子分母相除后的质因子相乘的形式。与博客相似：码蹄集2218--阶乘的质因子_sweet_Mary的博客-CSDN博客

再利用高精度*低精度求得最终的结果。与博客相似：码蹄集2197--个数统计_sweet_Mary的博客-CSDN博客

代码如下：

#include<bits/stdc++.h> 
using namespace std;

int up[100010];//分子
int down[100010];//分母
int final_[100010];//分子-分母
int m,n;
int max_up;//记录因子最大值--分子
int max_down;//记录因子最大值--分母
int max_final;
int a[100010];


//寻找因子
void change(int a[],int num,int& max_up_or_down){
    int temp=num;
    for(int i=2;i*i<=temp;i++){
        if(temp%i==0){
            while(temp%i==0){
                a[i]++;
                max_up_or_down=max(max_up_or_down,i);
                temp/=i;
            }
        }
    }
    if(temp!=0 and temp!=1){
        a[temp]++;
        max_up_or_down=max(max_up_or_down,temp);
    }

}

//高精度*低精度
//a*num==>c
void multiply(int num,int& len_){
    int c[100010]={0};
    for(int i=0;i<len_;i++){
        c[i]+=a[i]*num;
        if(c[i]>=10){
            c[i+1]=c[i]/10;
            c[i]%=10;
        }
    }
    while(c[len_]){
        if(c[len_]>=10){
            c[len_+1]+=c[len_]/10;
            c[len_]%=10;
        }
        len_++;
    }
    memcpy(a,c,sizeof(c));
}



int main( )
{   
    cin>>m>>n;
    for(int i=m+1;i<=m+n;i++){
        change(up,i,max_up);
    }
    for(int i=1;i<=n;i++){
        change(down,i,max_down);
    }
    for(int i=2;i<=max_up;i++){
        final_[i]=up[i]-down[i];
        if(final_[i]!=0){
            max_final=max(max_final,i);
        }
    }
    a[0]=1;
    int len_=1;
    for(int i=2;i<=max_final;i++){
        while(final_[i]){
            multiply(i,len_);
            final_[i]--;
        }
    }
    for(int i=99,k=1;i>=0;i--,k++){
        cout<<a[i];
        if(k==10){
            cout<<endl;
            k=0;
        }
    }
    return 0;
}