72. 编辑距离 - 力扣（LeetCode）

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数  。你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

 

编辑距离的应用场景：DNA的编辑，大段大段的DNA，找到几个关键的节点，做插入做替换，可能就能得到目标DNA了

>>思考和分析：

首先，对这个问题做一个定义，然后把这个问题进行分解。怎么分解呢？考虑它的最后一步，此题我们就考虑S1和S2的末尾字符是否相同，相同的话，我该怎么处理？不相同的话，插入删除替换这三种操作又会进入到什么问题思考？ 

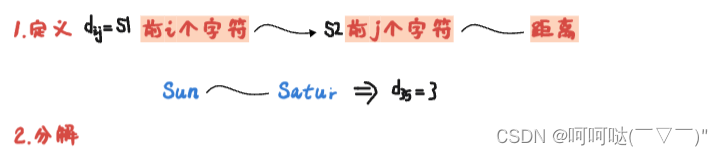
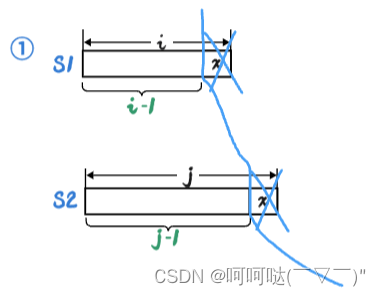
1.S1和S2的末尾字符相同，意味着可以剥离出去相同的，如图蓝色的线表示将x剥离出去。那么剩下要考虑的是S1的前i-1个字符如何编辑才能得到S2的前j-1个字符的问题(O_O)?

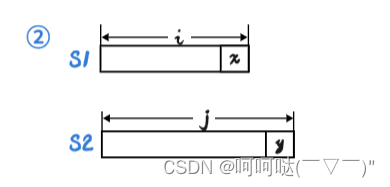
if(S1[i-1] == S2[j-1])
        dp[i][j] = dp[i-1][j-1];

2.S1和S2的末尾字符是不相同的，到底是插入，是删除，还是替换？

问题思考(O_O)?：如果我要进行插入操作，我是对谁进行操作？

其实是对S1操作，也只能对S1进行操作，也就是我认为S2的末尾是y，S1的末尾不是y，选择把y给插到S1的末尾。因为可能 S1的这 i 个字符 跟 S2的 j-1 个字符 其实是具有高度的相似性的，就是S1末尾缺了一个y。所以我选择插入

dp[i][j] = dp[i][j-1]+1;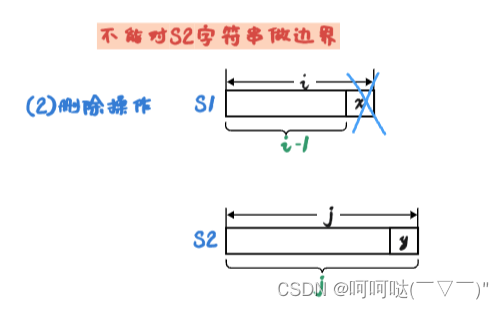

若执行删除操作，也只能对S1操作，我把S1的末尾给删掉，意味着 S1的前i-1个字符 和 S2的前j个字符 是具有高度的相似性的。就是仅仅因为S1的末尾多了个x，所以我把x删掉

dp[i][j] = dp[i-1][j]+1;

若执行替换操作，可能出现的场景。那可能是认为 S1的前i-1个字符 和 S2的前j-1个字符 具有高度的相似性，仅仅是S1的末尾字符是x，S2的末尾字符是y，只要把这个x换成y，就可以达到最优解！（一定要强调是对S1进行的操作）

dp[i][j] = dp[i-1][j-1]+1;

综上，可以得出这样的递推式：

if(S1[i-1] == S2[j-1])
    dp[i][j] = dp[i-1][j-1];
else
    dp[i][j] = min(dp[i][j-1]+1,dp[i-1][j]+1,dp[i-1][j-1]+1);

问题思考(O_O)?：我到底是进行插入、删除还是替换操作呢？比如说背包问题，我这件物品到底是放还是不放呢？其实对于算法而言，它当时并不知道，只知道按照这个方式进行分解就可以了，总之就是这么两种方式分解，没有什么别的选择方案！对于此题也是一样，要么插入、要么删除、要么替换，在这三种方案里面选一个，编辑距离选一个代价最小的，就可以了！

class Solution {
public:
    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
        for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
        for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
        for (int i = 1; i <= word1.size(); i++) {
            for (int j = 1; j <= word2.size(); j++) {
                if (word1[i - 1] == word2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1];
                }
                else {
                    dp[i][j] = min({dp[i - 1][j], dp[i][j - 1],dp[i - 1][j - 1]}) + 1;
                }
            }
        }
        return dp[word1.size()][word2.size()];
    }
};

文章和图文参考b站视频：

[轻松掌握动态规划]6.编辑距离_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1sA411B73r/?spm_id_from=333.880.my_history.page.click