强化学习概念

• Terminologies（术语）
  • State s：环境的一个状态
  • Agent ：代理
  • Action a：动作
  • Environment：代理外的其他东西
  • Reward r：反馈，代理从环境中收到的数值
  • Policies π(a|s)：策略是代理根据state来决定action
  • State transition p(s’|s,a)：状态转移函数
  • Trajectory：序列是代理和环境交互过程中的一系列状态和动作组成
• Return and Value
  • Return：回报，衡量当前时刻局势的好坏，未来的回报没当前汇报重要
    $$U_t=R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+\dots$$
  • Action-Value Function：近似Ut，依据动作
    $$Q_{\pi }(s_t,a_t)=\mathbb{E}[U_t|s_t,a_t]$$
  • Optimal action-value function:
    $$Q^{\ast }(s_t,a_t)=\max Q_{\pi }(s_t,a_t)$$
  • State-Value Function：近似Ut，依据策略
    $$V_{\pi }(s_t)={\mathbb{E}}_A[Q_{\pi }(s_t,A)]$$
• Value-based learning.对选择的动作进行评分
  • Deep Q network (DQN) for approximating Q*(s, a).
  • Learn the network parameters using temporal different (TD).
• Policy-based learning.计算选择某动作的概率
  • Policy network for approximating π(a | s).
  • Learn the network parameters using policy gradient.
• Actor-critic method. (Policy network value network.
  Example: AlphaGo

Model-Free

Value-based learning

DQN

• 目标：最大化return
• 问题：如果我们知道价值函数Q^*，什么是最好的action？
• 挑战：Q^*是什么？
  • 使用神经网络Q去近似Q^*
• 时间差分学习(temporal-difference learning)

Definition: Optimal action-value function.

• Q*(s_t, a_t) = max_πE[U_t|S_t = s_t, A_t = a_t].
• DQN: Approximate Q*(s, a)using a neural network (DQN).
• Q(s, a; w)is a neural network parameterized by w.
• Input: observed state s.
• Output: scores for every actien a ∈ A.

Step1：观察状态St和动作At。
Step2：预测值函数：V(St, At) = f(St, At; w)，其中f是具有参数w的值网络。
Step3：对值网络进行微分：∇w V(St, At) = ∇w f(St, At; w)。
Step4：环境提供新的状态St+1和奖励Rt。
Step5：计算TD目标：Yt = Rt + γ * maxa Q(St+1, a; w)，其中γ是折扣因子，Q是动作值函数。
Step6：执行梯度下降来更新参数：w’ = w - α * (V(St, At) - Yt) * ∇w f(St, At; w)，其中α是学习率。
Step7：更新值网络的参数：w = w’。

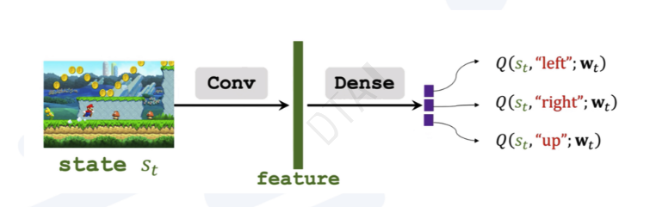
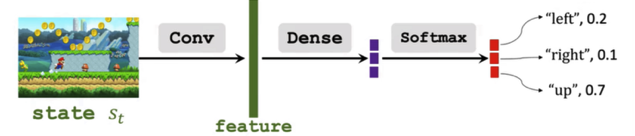
State-based learning

策略函数π(a | s)是一个概率密度函数，它接受一个状态（state）作为输入，并输出代理（agent）可以采取所有动作（action）的概率。例如：

π(left | s) = 0.2
π(right | s) = 0.1
π(up | s) = 0.7

类似于基于价值的学习，我们可以使用神经网络来近似这个策略函数。

使用策略网络（π(a | s; θ)）来逼近策略函数π(a | s)。
θ表示神经网络的可训练参数。

步骤：

• Algorithm: Policy Gradient with Approximate Policy Gradient Theorem

  • Step1：Observe the state st.
  • Step2：Randomly sample action at according to the policy network π(at | st; θ).
  • Step3：Compute the estimated action-value Q(st, at).
  • Step4：Differentiate the policy network: ∇θ π(at | st; θ).
  • Step5：Compute the (approximate) policy gradient: g(at, θ) = Q(st, at) * ∇θ π(at | st; θ).
  • Step6：Update the policy network parameters: θ’ = θ + β * g(at, θ).

• 算法：使用近似策略梯度定理的策略梯度方法

• Step1：观察状态st。
• Step2：根据策略网络π(at | st; θ)随机采样动作at。
• Step3：计算估计的动作值Q(st, at)。
• Step4：对策略网络进行微分：∇θ π(at | st; θ)。
• Step5：计算（近似）策略梯度：g(at, θ) = Q(st, at) * ∇θ π(at | st; θ)。
• Step6：更新策略网络的参数：θ’ = θ + β * g(at, θ)。

蒙特卡洛近似

• 利用大数定理，来做期望的近似
  

Actor-Critic Learning

• 目标函数还是状态价值函数（状态的期望），不过值（演员）和概率（评论家）都需要用神经网络去拟合
• 
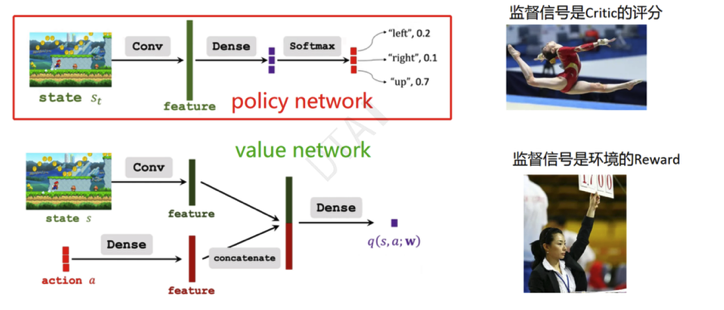
• 步骤：
  • Step1：观察状态 st。
  • Step2：根据策略 r(·, st; θ) 随机采样动作 at。
  • Step3：执行动作 at，并观察新的状态 st+1 和奖励 rt。
  • Step4：使用时序差分（Temporal Difference, TD）更新值网络（value network）的参数 w。
  • Step5：使用策略梯度（policy gradient）更新策略网络（policy network）的参数 θ。

Model-Based

• AlphaGo Zero 使用191917的张量表示一个状态，8个矩阵是白子的格局，8个矩阵是黑子的格局，1个矩阵代表如果该落黑子，表示全部元素等于1，如果该落白子，该矩阵全部元素等于0。

Monte Carlo TreeSearch(MCTS)-AlphaGo

• 假设此时已经训练好了策略网络T(a l s;θ)和价值网络v(s;w)。 AlphaGo真正跟人下棋的时候，做决策的不是策略网络或者价值网络，而是蒙特卡洛树搜索(MonteCarloTreeSearch)，缩写MCTS。MCTS不需要训练，可以直接做决策。训练策略网络和价值网络的目的是辅助MCTS。

• 人类玩家通常都会向前看几步；越是高手，看得越远。

• MCTS的基本原理就是向前看，模拟未来可能发生的情况，从而找出当前最优的动作。AlphaGo每走一步棋，都要用MCTS做成千上万次模拟，从而判断出哪个动作的胜算最大。

• 步骤：

  • Step1：选择：观测棋盘上当前的格局，找出所有空位，然后判断其中哪些位置符合围棋规则；每个符合规则的位置对应一个可行的动作。每一步至少有几十、甚至上百个可行的动作；假如挨个搜索和评估所有可行动作，计算量会大到无法承受。虽然有几十、上百个可行动作，好在只有少数几个动作有较高的胜算。选择（Selection）的目的就是找出胜算较高的动作，只搜索这些好的动作，忽略掉其他的动作。
  • Step2：拓展：把第一步选中的动作记作at，它只是个假想的动作。AlphaGo需要考虑这样一个问题：假如它执行动作at，那么对手会执行什么动作呢？AlphaGo可以“推己及人”：如果AlphaGo认为几个动作很好，对手也会这么认为。所以AlphaGo用策略网络模拟对手，根据策略网络随机抽样一个动作。
  • Step3：求值：从状态st+1开始，双方都用策略网络π做决策，在环境中交替落子，直到分出胜负。AlphaGo基于状态sk，根据策略网络抽样得到动作。对手再基于动作，观测到的棋盘上的新状态再根据策略网络抽样得到新动作，直到游戏结束。当这局游戏结束时，可以观测到奖励r。如果AlphaGo胜利，则r=+1，否则r=-1。状态st+1越好，则这局游戏胜算越大。因此，奖励r可以反映出st+1的好坏。此外，还可以用价值网络v评价状态st+1的好坏。价值v（st+1；w）越大，则说明状态st+1越好。
  • Step4：回溯：再第三步求值中，算出了第t+1步某一个状态的价值，记作V（st+1）；每一次模拟都会得出这样一个价值，并且记录下来。模拟会重复很多次，于是第t+1步每一种状态下面可以有多条记录；第t步的动作at下面有多个可能的状态（子节点），每个状态下面有若干条记录。把at下面所有的记录取平均，记作价值Q（at），它可以反映出动作at的好坏。
    给定棋盘上的真实状态st，有多个动作a可供选择。对于所有的a，价值Q（a）的初始值是零。动作a每被选中一次（成为at），它下面就会多一条记录，我们就对Q（a）做一次更新。基于棋盘上真实的状态st，MCTS需要从可行的动作中选出一个，作为at。MCTS计算每一个动作a的分数：

• 原理推导比较多，还没懂，估计后面用不到就不细看了，有用到再回来补一下这部分知识

• 强化学习是机器学习中最难的一部分之一