3.1 Tensor中统计学有关的函数

3.1.1 平均值、总和、累积

1.测试结果1

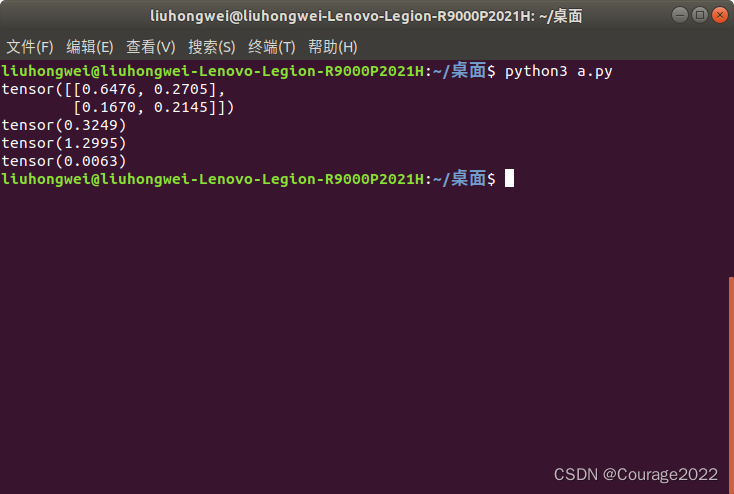
import torch

a = torch.rand(2, 2)

print(a)
print(torch.mean(a,))
print(torch.sum(a))
print(torch.prod(a))

2.测试结果2： $2 \times 3$ 数组对第1维操作

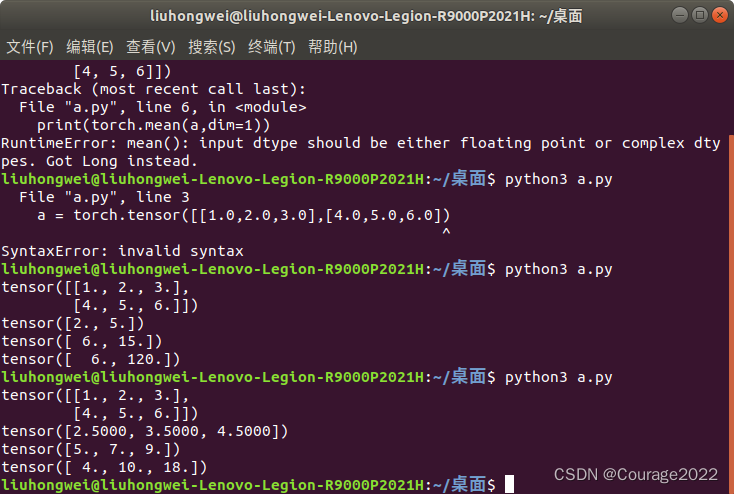
import torch

a = torch.tensor([[1.0,2.0,3.0],[4.0,5.0,6.0]])

print(a)
print(torch.mean(a,dim=1))
print(torch.sum(a,dim=1))
print(torch.prod(a,dim=1))

3.测试结果3： $2 \times 3$ 数组对第0维操作

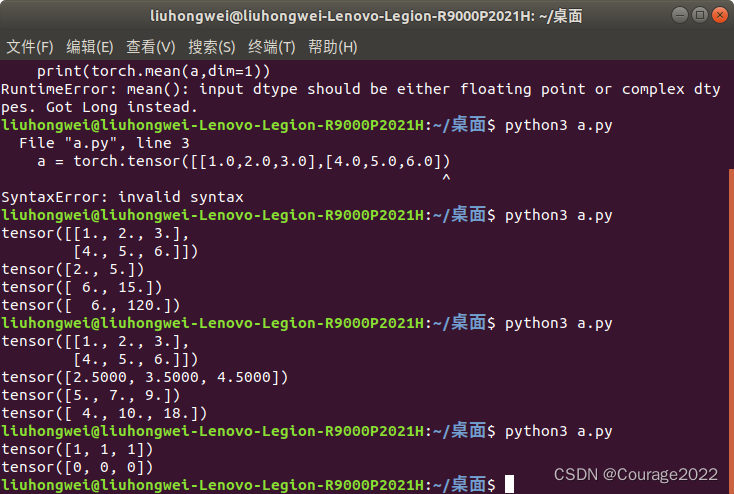
import torch

a = torch.tensor([[1.0,2.0,3.0],[4.0,5.0,6.0]])

print(a)
print(torch.mean(a,dim=0))
print(torch.sum(a,dim=0))
print(torch.prod(a,dim=0))

3.1.2 返回最值排序的索引值

import torch

a = torch.tensor([[1.0,2.0,3.0],[4.0,5.0,6.0]])

print(torch.argmax(a,dim=0))
print(torch.argmin(a,dim=0))

3.1.3 标准差、方差、中间数、众数

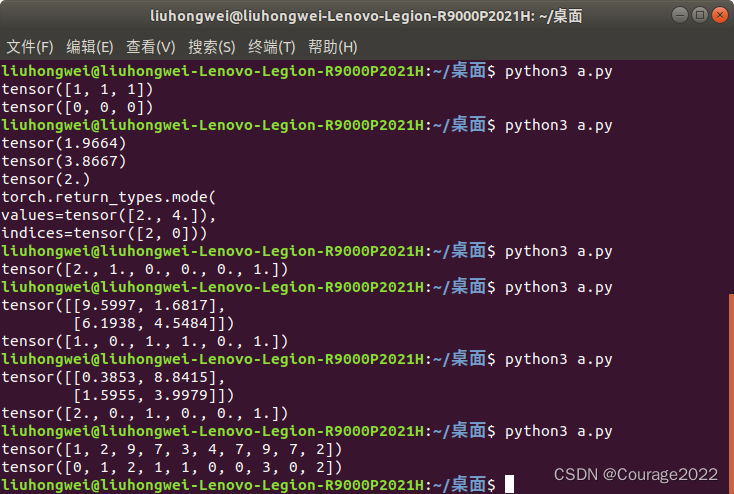
import torch

a = torch.tensor([[1.0,2.0,2.0],[4.0,5.0,6.0]])

print(torch.std(a))
print(torch.var(a))
print(torch.median(a))
print(torch.mode(a))

3.1.4 计算input的直方图

import torch

a = torch.rand(2,2)*10
print(a)
print(torch.histc(a,6,0,0))
第二个参数是指将数据分成几个区间，第三个参数第四个参数默认是0表示以a中最小的值作为初始区间，最大的值作为结束区间。演示结果如下图：

3.1.5 返回频数（只支持一位tensor）

import torch

a = torch.randint(0,10,[10])
print(a)
print(torch.bincount(a))
0出现了..次，1出现了..次.....可以用来统计某一样别样本数量

3.1.6 分布函数torch.distributions

3.1.7 tensor中的随机抽样函数

用随机数种子能够保证每次抽样的结果是一样的：
import torch

torch.manual_seed(1)

mean = torch.rand(1,2)
std = torch.rand(1,2)

print(torch.normal(mean,std))

3.2 tensor中与线性代数有关函数

3.2.1 tensor中的范数运算

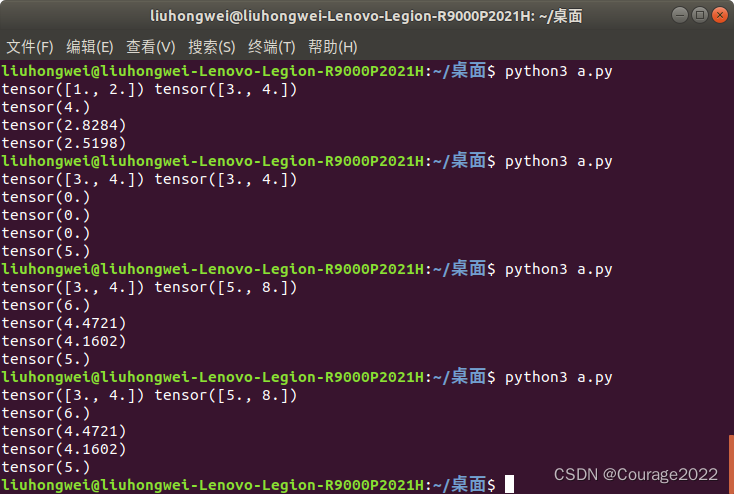
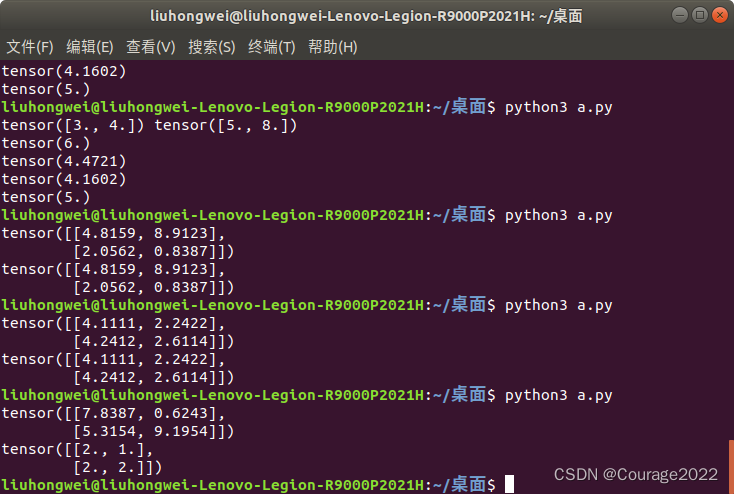
$\sum |a-b|,\sum \sqrt{(a-b)^{2}},\sum \sqrt{(a-b)^{3}}$ norm:平方和相加开根号

import torch

a = torch.tensor([3.0,4.0])
b = torch.tensor([5.0,8.0])

print(a,b)
print(torch.dist(a,b,p=1))
print(torch.dist(a,b,p=2))
print(torch.dist(a,b,p=3))

print(torch.norm(a))

3.2.2 tensor与矩阵分解

3.2.2.1 矩阵分解介绍

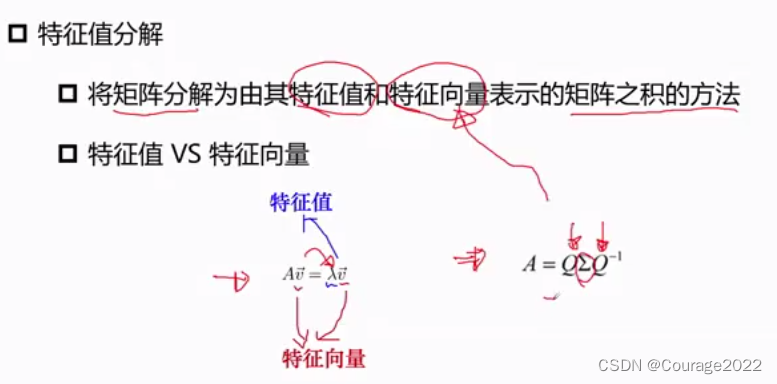
3.2.2.2 EVD分解

考研的时候考过，不细说。 $Q$ 是特征向量矩阵， $\Sigma$ 是特征值矩阵。要求矩阵满秩。

PCA与特征值分解（主成分分析）：通过一个投影矩阵，将原始的 $n \times m$ 维特征矩阵(n个特征m个样本，即每一个样本表示成n维向量)映射到k维（最终结果为 $k \times m$ ）上去（通过投影矩阵 $k \times n$ 来实现映射）来实现降维。

3.2.2.3 SVD分解

        由于EVD分解只针对满秩矩阵且必须是方阵，我们引出了SVD分解，对矩阵形状和秩没有要求。

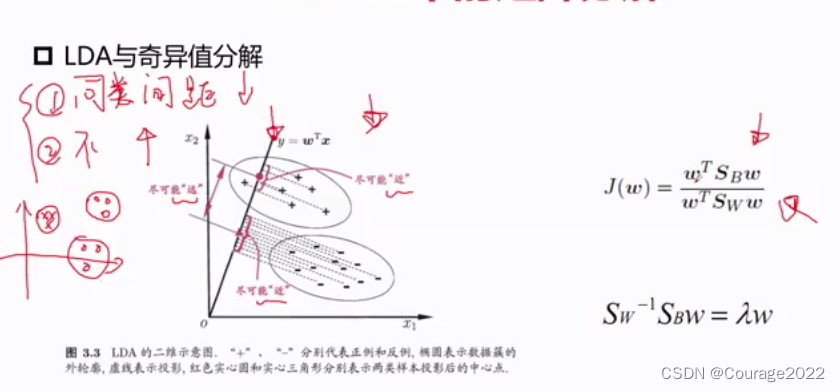
         应用：LDA算法中，主要思想是在"新空间"让同类物体的间隔尽可能小，不同类别物体的间隔尽可能大。

          $S_{B}$ 描述为同类物体的协方差矩阵， $S_{W}$ 描述为不同类物体的协方差矩阵。优化目标是对代价函数求最大值。

3.3 pytorch

3.3.1 Tensor的裁减运算

对tensor中元素进行范围性的约束，一是将数据约束在比较小的范围中网络在参数学习中容易稳定，可以实现类似正则化的功能防止过拟合；二是防止梯度离散/梯度爆炸。
import torch

a = torch.rand(2,2)*10
print(a)

print(a.clamp(1,2))   #将数据处理到1-2之间
 

3.3.2 tensor的索引与数据筛选

3.2.2.1 torch.where

第一个参数是判断条件，如果满足判断条件选择第二个参数的数据，如果不满足选择第三个参数的数据。类似C++中的 a>b?a:b
import torch


a = torch.rand(4,4)
b = torch.rand(4,4)

print(a)
print(b)

out = torch.where(a>0.5,a,b)
print(out)

3.2.2.2 torch.index_select

我们用代码进行分析：
Chapter3 Pytorch与机器学习有关函数（一）

我们初始化了一个 $4\times 4$ 的张量，我们取出了第0、3、2行的数据到张量out中。

3.2.2.3 torch.gather

我们用代码进行分析：
import torch


a = torch.linspace(1,16,16).view(4,4)
print(a)

out  = torch.gather(a,dim=0,index=torch.tensor([[0,1,1,1],[0,1,2,2],[0,1,3,3]]))
print(out)
我们初始化了一个 $4\times 4$ 的张量，分别在第0维上找第 0 1 1 1个数据，即1 6 7 8，然后再取0 1 2 2 个数据......

如果维度更高那么gather怎么用呢？

3.2.2.4 torch.masked_select

import torch


a = torch.linspace(1,16,16).view(4,4)
print(a)

mask = torch.gt(a,8)
print(mask)

out  = torch.masked_select(a,mask)
print(out)

很好理解，不多解释。

3.2.2.5 torch.take

import torch

a = torch.linspace(1,16,16).view(4,4)
print(a)

out = torch.take(a,index = torch.tensor([0,15,13,10]))
print(out)

很好理解，不多解释。

3.3.3 tensor的组合和拼接

3.3.3.1 torch.cat

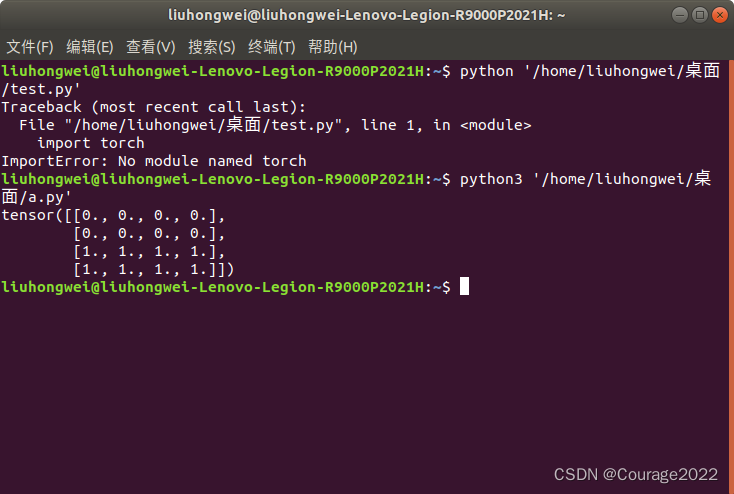
import torch

a = torch.zeros((2,4))
b = torch.ones((2,4))

out = torch.cat((a,b),dim = 0)
print(out)
我们看到我们在第0维上进行了拼接，原来是两个 $2\times 4$ ，拼接完成变成了 $4\times 4$ 的张量。

我们再将维度修改成1，查看其运行结果。

3.3.3.2 torch.stack

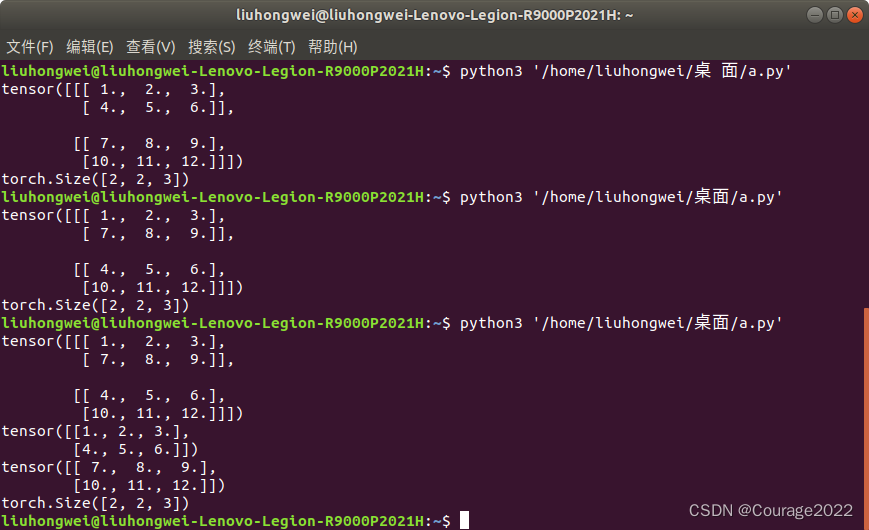
import torch

a = torch.linspace(1,6,6).view(2,3)
b = torch.linspace(7,12,6).view(2,3)

out = torch.stack((a,b),dim = 0)
print(out)
print(out.shape)
         我们来解析一下这个size：

[[[ 1., 2., 3.],         [ 4., 5., 6.]],        [[ 7., 8., 9.],         [10., 11., 12.]]]

        第一维度就有两个数据：[[ 1., 2., 3.], [ 4., 5., 6.]]，[[ 7., 8., 9.], [10., 11., 12.]]

        第二维度也是两个数据[ 1., 2., 3.], [ 4., 5., 6.]

        第三维度是三个数据1，2，3

        因此这个shape是 $2\times 2 \times 3$ 的形式。

        而a是[ [1,2,3] ,[4,5,6]]的 $2\times 3$ 形式，将a和b看作是两个独立的元素在第0维度进行拼接。

        那么如果在第一维度拼接是个什么样的结果呢？
import torch

a = torch.linspace(1,6,6).view(2,3)
b = torch.linspace(7,12,6).view(2,3)

out = torch.stack((a,b),dim = 1)
print(out)

print(out[:,0,:])
print(out[:,1,:])

print(out.shape)
那么如果在第二维度拼接是个什么样的结果呢？
import torch

a = torch.linspace(1,6,6).view(2,3)
b = torch.linspace(7,12,6).view(2,3)

out = torch.stack((a,b),dim = 2)
print(out)

print(out[:,:,0])
print(out[:,:,1])

print(out.shape)

3.3.4 tensor的切片

3.3.4.1 torch.chunk

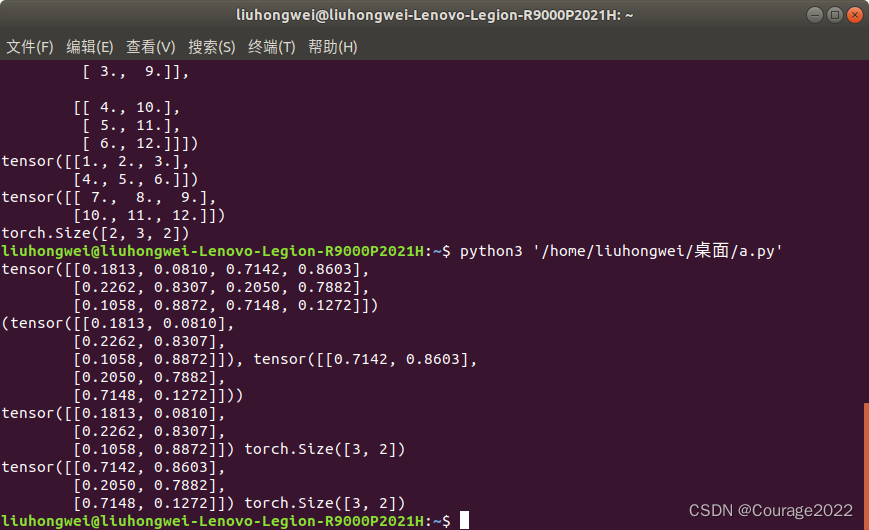
import torch

a = torch.rand((3,4))
print(a)

out = torch.chunk(a,2,dim=1)
print(out)

print(out[0],out[0].shape)
print(out[1],out[1].shape)
        对第一维度进行分割，即

        [[0.1813, 0.0810, 0.7142, 0.8603],
        [0.2262, 0.8307, 0.2050, 0.7882],
        [0.1058, 0.8872, 0.7148, 0.1272]]

        对大括号里面进行分割，我们一个括号选出两个组成新的张量，构成两个 $3\times 2$ 的张量。

3.3.4.2 torch.split

1.和torch.chunk一样的调用方式

import torch

a = torch.rand((3,4))
print(a)

out = torch.split(a,2,dim=1)
print(out)

print(out[0],out[0].shape)
print(out[1],out[1].shape)

2.不平均分割

import torch

a = torch.rand((10,4))
print(a)

out = torch.split(a,3,dim=0)
print(len(out))

for t in out:
	print(t,t.shape)

3.第二种调用方式：传入list列表，指定我们要切分的尺寸

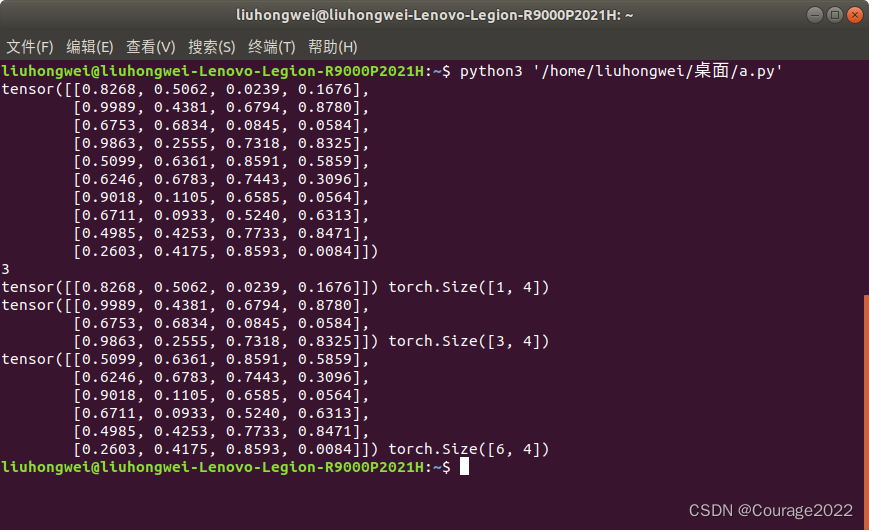
import torch

a = torch.rand((10,4))
print(a)

out = torch.split(a,[1,3,6],dim=0)
print(len(out))

for t in out:
	print(t,t.shape)

3.3.5 tensor的变形操作

3.3.5.1 tensor.reshape

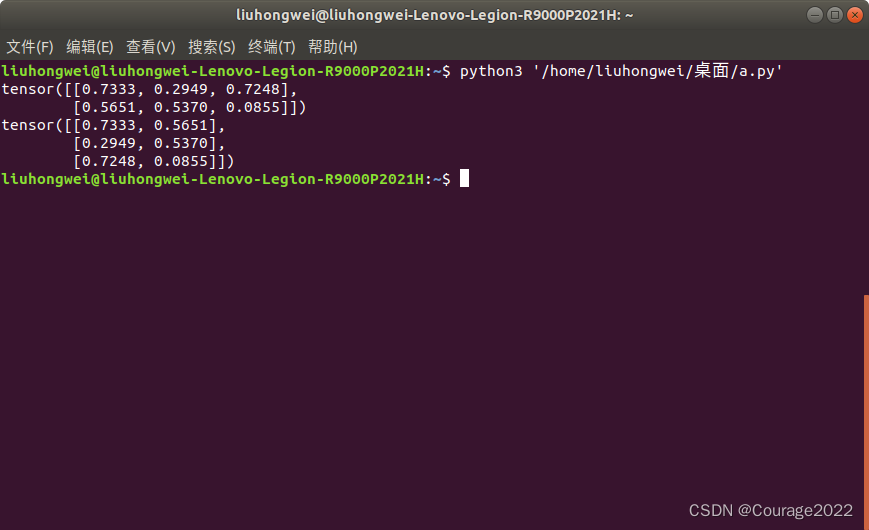
import torch

a = torch.rand((2,3))
print(a)

out = torch.reshape(a,(3,2))
print(out)
简单来说，就是进行了简单的排列组合。

3.3.5.2 torch.t

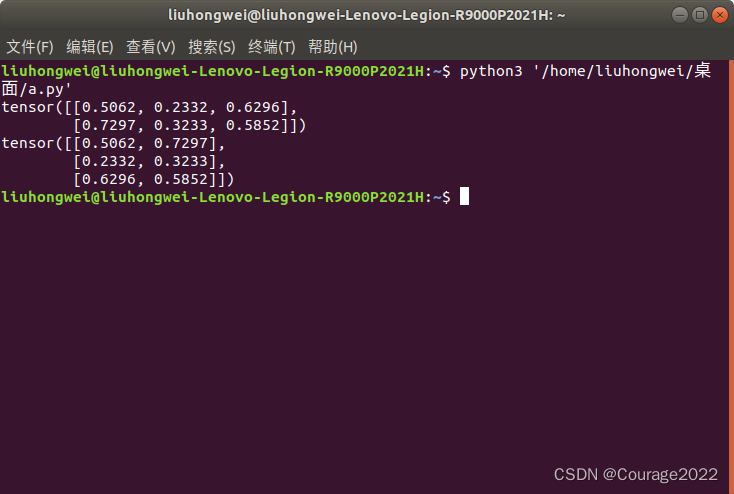
import torch

a = torch.rand((2,3))
print(a)

out = torch.t(a)
print(out)

对张量进行矩阵运算。

3.3.5.3 torch.transpose

1.用transpose求转置

将两个维度相互交换：
import torch

a = torch.rand((2,3))
print(a)

out = torch.transpose(a,0,1)
print(out)
交换a张量的第0维和第一维，相当于求转置。

2.用transpose实现高维交换

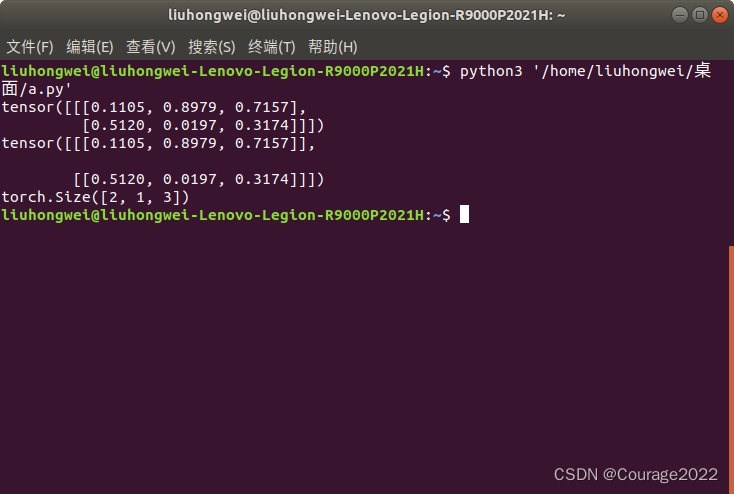
import torch

a = torch.rand((1,2,3))
print(a)

out = torch.transpose(a,0,1)
print(out)
print(out.shape)

3.3.5.4 torch.squeeze

去除维度为1的维度。

import torch

a = torch.rand((1,2,3))
print(a)


out = torch.squeeze(a)
print(out)
print(out.shape)

3.3.5.5 torch.unsqueeze

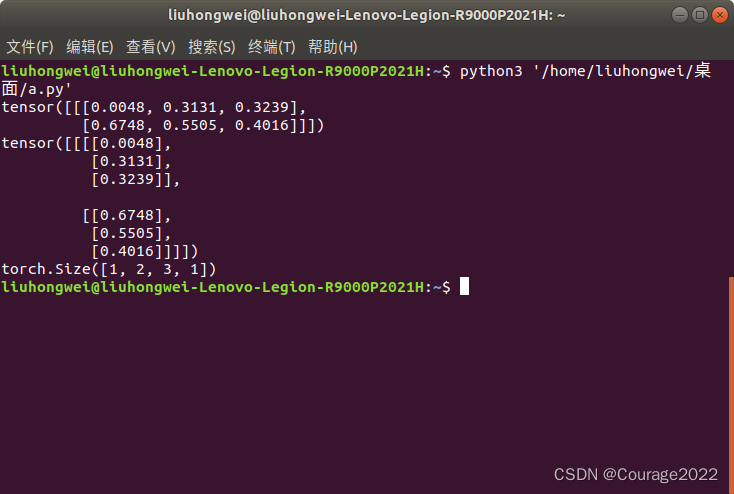
-1表示在最后一个维度进行拓展。

import torch

a = torch.rand((1,2,3))
print(a)


out = torch.unsqueeze(a,-1)
print(out)
print(out.shape)

3.3.5.6 torch.unbind

对维度进行删除，类似于tensor切分的过程：我们会拿到元组，和我们切分拿到的元组类似。
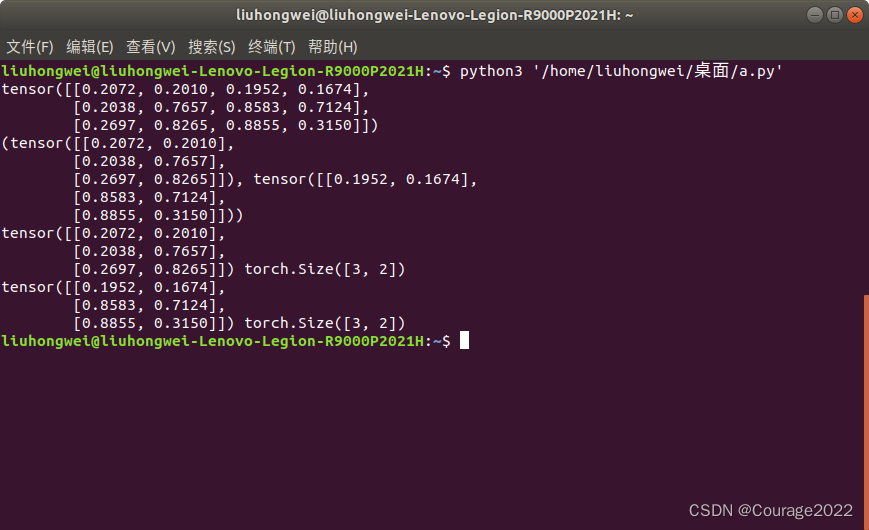
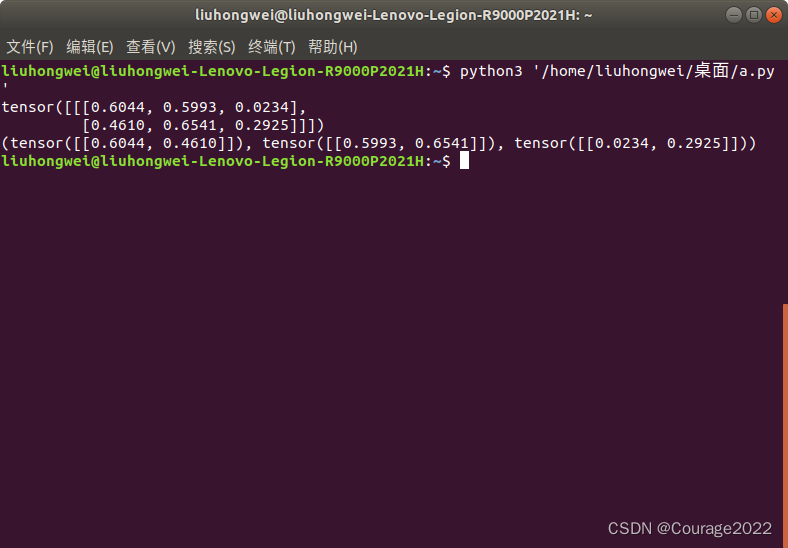
import torch

a = torch.rand((1,2,3))
print(a)


out = torch.unbind(a , dim=1)
print(out)
tensor([[[0.4037, 0.2314, 0.8198], [0.5632, 0.1900, 0.5313]]]) $1 \times 2 \times 3$
(tensor([[0.4037, 0.2314, 0.8198]]), tensor([[0.5632, 0.1900, 0.5313]])) $(1 \times 3 ) * 2$

若对第三维进行切分，结果如下： $(1 \times 2) *3$