前言

最近看了些Open Winding永磁同步电机及其控制策略的文献资料，现做个总结。未来的研究方向也大概率围绕Open Winding开展，期待同行交流学习。

简介

开绕组(Open Winding)电机指把传统的交流电机的三相定子绕组的中性点X/Y/Z打开，这样具有六个接线端子结构的电机即开绕组电机。这样的结构的电机具有高直流电压利用率、更好的容错性能、多电平调制和高转矩密度的优点，因而广泛应用于电动汽车动力系统以及风力发电等场景。

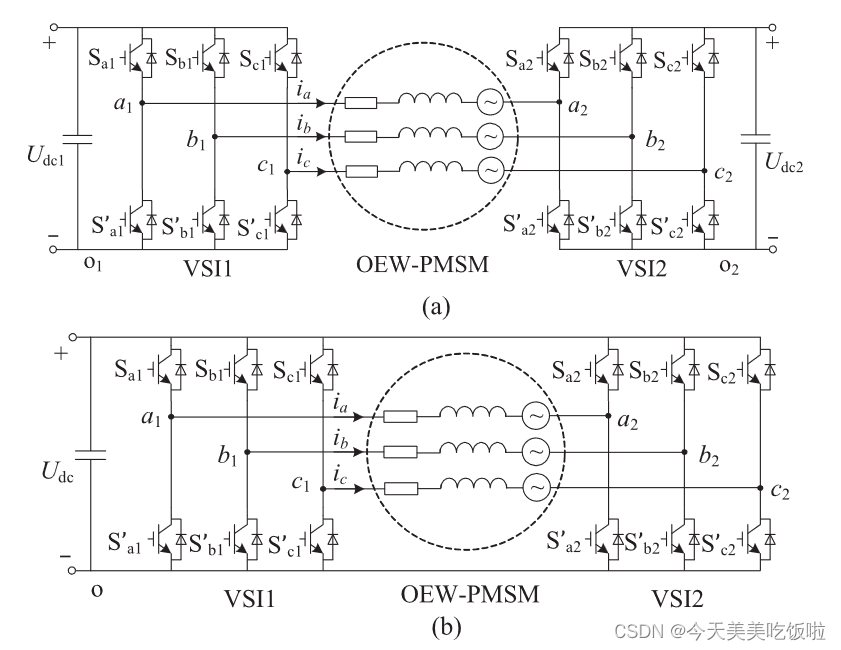
Open Winding电机的驱动拓扑，据逆变器直流侧可以分为隔离直流母线isolated dc bus和共直流母线common dc bus两种类型。

• 隔离直流母线有两个电源，不存在零序通路，因而不必考虑这种拓扑的零序抑制问题。且两个电源的电压等级可以不同，因而存在更多控制的灵活性。缺点在于系统的体积会较共直流母线的拓扑更为庞大。
• 共直流母线的拓扑只有一个电源，存在零序通路，但该种拓扑结构更为简洁，能量密度更高，因而大多数的研究均围绕common dc bus开展，主要研究零序电流的抑制。

从个人观点来看，共直流母线确实更吸引我，至今阅读的文献也都是共直流母线的拓扑，下文提及的Open Winding电机的拓扑均为共直流母线拓扑。

Open Widing电机数学模型

在abc坐标系下Open Winding电机的数学模型与传统的三相电机的数学模型完全相同，唯一不同在于需要考虑零序的影响。因此经park变换到旋转坐标系以后，零序分量不能忽略，必须加以考虑。

旋转坐标系下的电压方程以及转矩方程为：
$\left[\begin{array}{c}{u}_d\\ u_q\\ u_0\end{array}\right]$=$\left[\begin{array}{ccc}p{L}_d+R_s& & \\ & p{L}_q+R_s& \\ & & p{L}_0+R_s\end{array}\right]$$\left[\begin{array}{c}{i}_d\\ i_q\\ i_0\end{array}\right]$+$\left[\begin{array}{c}0\\ {\omega }_e{\psi }_{f1}\\ -3{\omega }_e{\psi }_{f3}sin(3{\theta }_e)\end{array}\right]$

$T_e=\frac{3}{2}{n}_p[i_q{\psi }_{f1}+(L_d-L_q)i_d{i}_q-6i_0{\psi }_{f3}sin(3{\theta }_e)]$

其中，$L_d,L_q,L_0$分别为d/q/0轴的等效电感，$R_s$为每相绕组的等效电阻，${\omega }_e$为电机电旋转角速度，${\psi }_{f1},{\psi }_{f3}$分别为永磁体的磁链的基波分量以及三次谐波分量。记$e_0=-3{\omega }_e{\psi }_{f3}sin(3{\theta }_e)$，称$e_0$为Open Winding电机的零序反电动势。

从转矩方程可以看出，与传统的PMSM电机的转矩方程相比，多出了零序电流的贡献部分，且该部分正比于永磁体磁链的三次谐波以及与三倍电角度的正弦值有关。常规的永磁电机在制造时，通常有意保留永磁体的三次谐波谐波来提高电机的转矩密度，因此${\psi }_{f3}\ne 0$，因此零序电流的存在会显著影响电磁转矩，从而造成转矩脉动。这是共直流母线电压最为显著的问题，因而绝大多数共直流母线开绕组电机的研究均围绕零序电流的抑制开展。

零序模型

从零序电压方程中可以看出，$u_0=R_s{i}_0+L_0\frac{d{i}_0}{dt}+e_0$，因此可以画出零序等效电路。

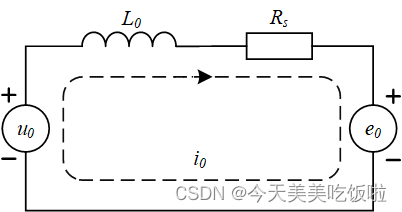
显然零序等效电路中有两个电压源，分别为$u_0,e_0$。其中$u_0$是逆变器经调制施加到OpenWinding电机机端上等效的零序电压(Zero Sequence Voltage,ZSV)，在一些文献中也称为共模电压(Common Mode Voltage, CMV)；$e_0$是电机的零序反电动势，根据dq0坐标系下的电压方程可知，$e_0=-3{\omega }_e{\psi }_{f3}sin(3{\theta }_e)$，是一个与磁链的三次谐波以及三倍电角度正弦值有关的变量。而前文已提到电机制造时会有意保留磁链的三次谐波，因此${\psi }_{f3}\ne 0$，$e_0$不会恒为0。

因此若要达到消除或抑制零序电流$i_0$的效果，只能从共模电压$u_0$入手，施加一定的控制，使得$u_0\approx e_0$，从而抑制零序电流$i_0$。

双逆变器调制

由于Open Winding将电机绕组中性点X/Y/Z打开，可以将ABC三相绕组的一端a1,b1,c1接入逆变器1，而三相绕组的另一端a2,b2,c2接入逆变器2，为了使得电机的正常运行，做到两个逆变器的电压矢量，分别记为$u_{s1},u_{s2}$合称为一个矢量圆$u_s$即可。

根据传统电机电压矢量，两个逆变器的电压矢量可以用下图表示，其中左图为逆变器1的电压矢量$u_{s1}$，右图为逆变器2的电压矢量$u_{s2}$。

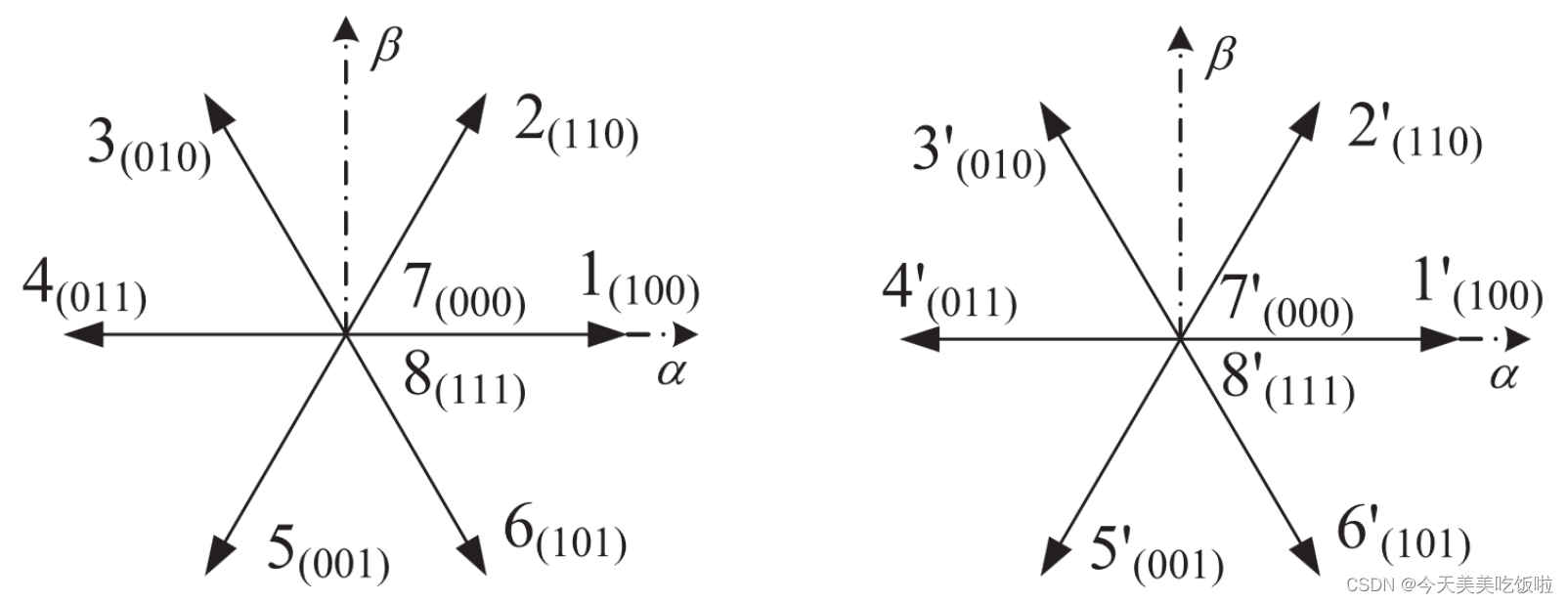
根据开绕组电机的特性，施加到开绕组电机上的合成电压矢量$u_s=u_{s1}-u_{s2}$，即用左图的电压矢量减去有图的电压矢量，得到的结果即双逆变器调制的电压矢量分布，结果如下图所示。

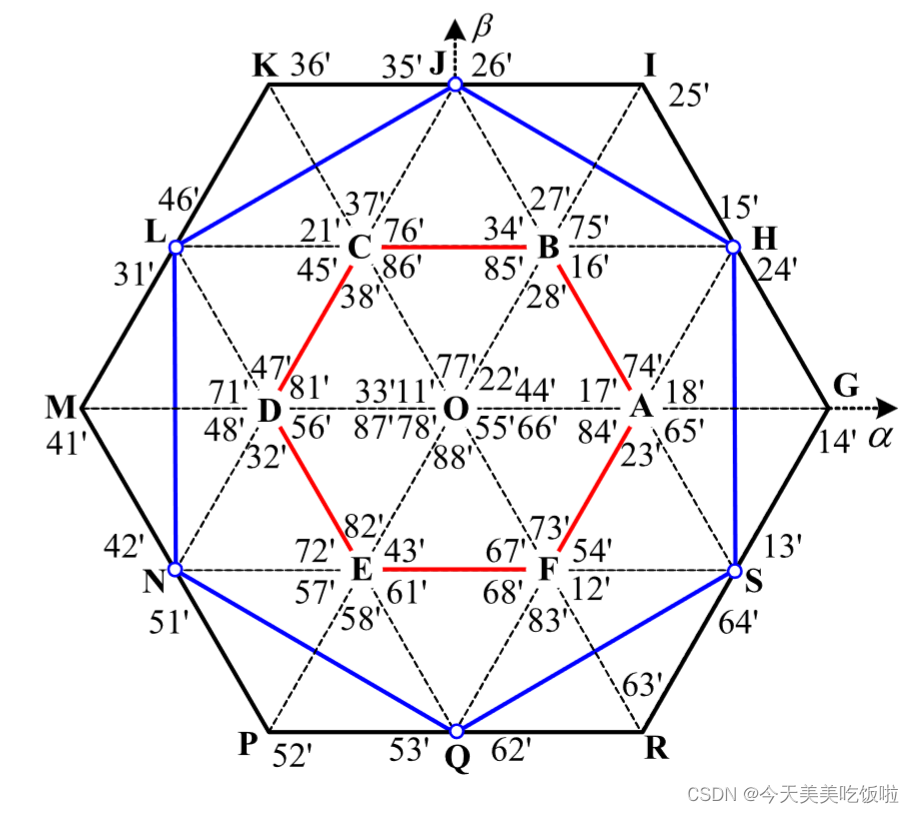
由最终的合成电压矢量图可以看出，双逆变器调制有三种六边形调制方式：

• 六边形ABCDEF，也称为内六边形调制，直流电压利用率最低，几乎不采用该种调制方式
• 六边形HJLNQS，也称为中间六边形调制，120度解耦调制，直流电压利用率较高，且不会因为调制产生共模电压。
• 六边形GIKMPR，也称为最大六边形调制，180度解耦调制，直流电压利用率最高，但会因为调制产生共模电压。

还有其他的调制方式，比如六边形钳位，但相较于前面提及的120度解耦调制与180度解耦调制相比实现方式更为复杂。

零序电流抑制基本思路

回到上文提到的内容，开绕组电机控制的首要目标是抑制零序电流，从零序等效电路模型出发，即需要灵活的控制由逆变器调制引起的共模电压CMV近似跟踪零序反电动势。120度解耦调制不会引入共模电压，即$u_0\equiv 0$，零序电路中只有零序反电动势，具有非常大的零序环流；180度解耦会引入共模电压，但共模电压完全取决于SVPWM调制发波引入，不施加一定的控制，并不能做到$u_0\approx e_0$，同样不能抑制零序环流。

传统的SVPWM只需要根据两相静止坐标系下的$u_{\alpha },u_{\beta }$即可生成SVPWM，为了使得SVPWM调制出的共模电压可控，需要另外引入一个控制变量$u_0$，进而调节零矢量的调节时间，达到调制出的共模电压可控的效果。而这种引入第三个控制变量的SVPWM多用于开绕组电机的零序电流抑制，在多数文献中也称为三维调制。引入的控制变量$u_0$为零序电压指令值，由零序电流控制器产生，通常设置为PI或者PR控制器。