基本原理

连通图中的每一棵生成树，都是原图的一个极大无环子图，即：从其中删去任何一条边，生成树就不在连通；反之，在其中引入任何一条新边，都会形成一条回路。
若连通图由n个顶点组成，则其生成树必含n个顶点和n-1条边。因此构造最小生成树的准则有三条：

1. 只能使用图中的边来构造最小生成树
2. 只能使用恰好n-1条边来连接图中的n个顶点
3. 选用的n-1条边不能构成回路

构造最小生成树的方法：Kruskal算法和Prim算法。这两个算法都采用了逐步求解的贪心策略。

Kruskal算法

核心思想：每次迭代时，选出一条具有最小权值，且连接后图不形成回路，加入生成树。

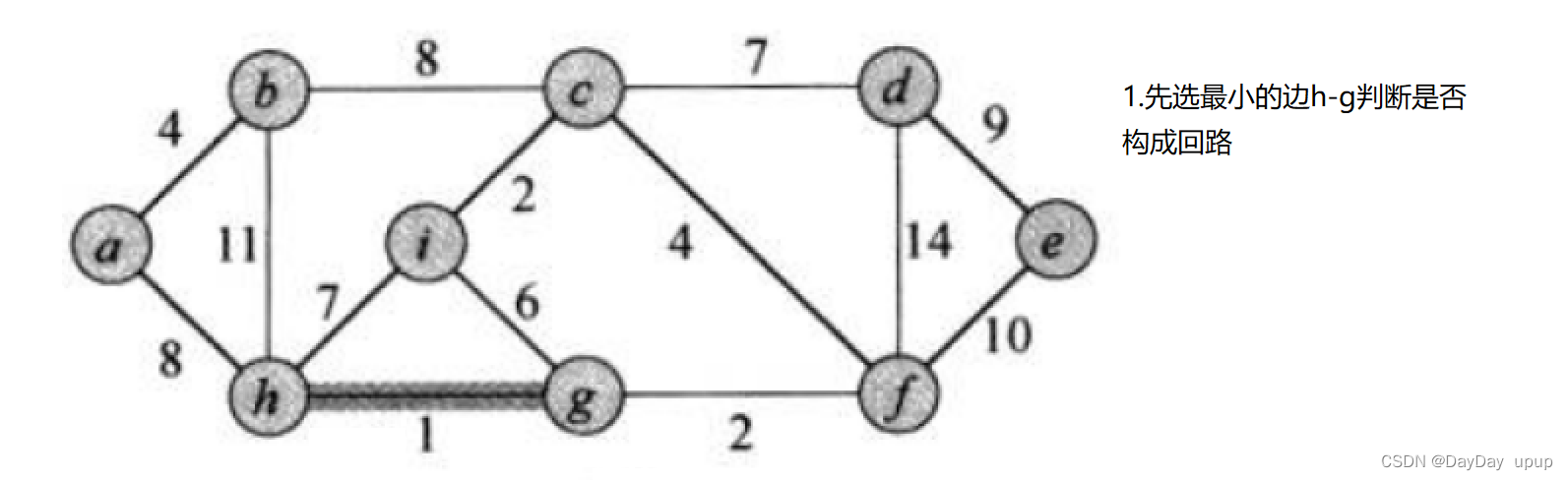
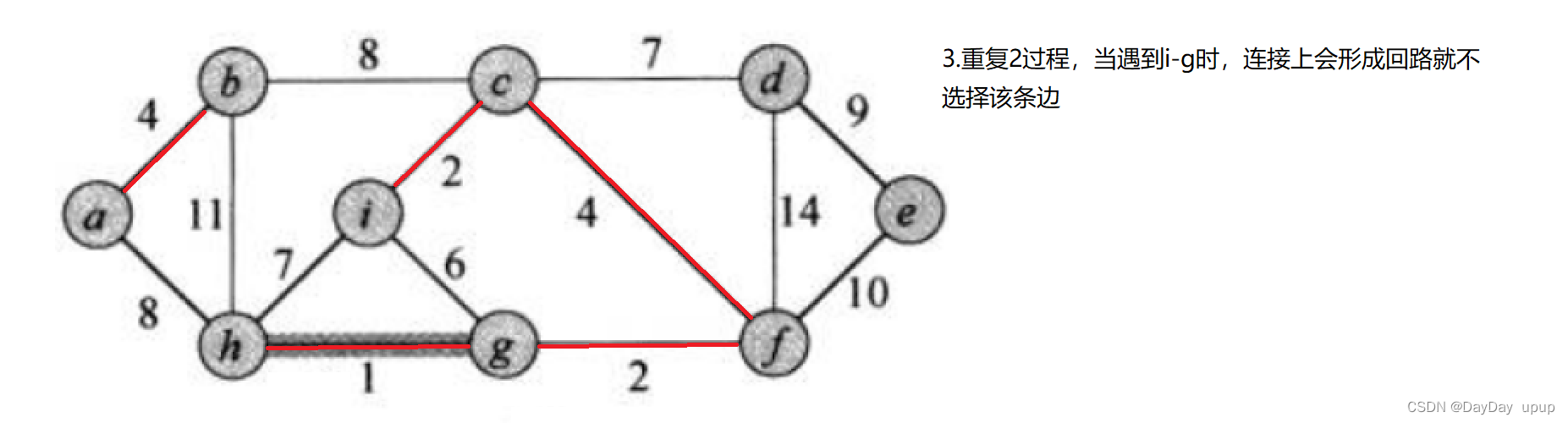
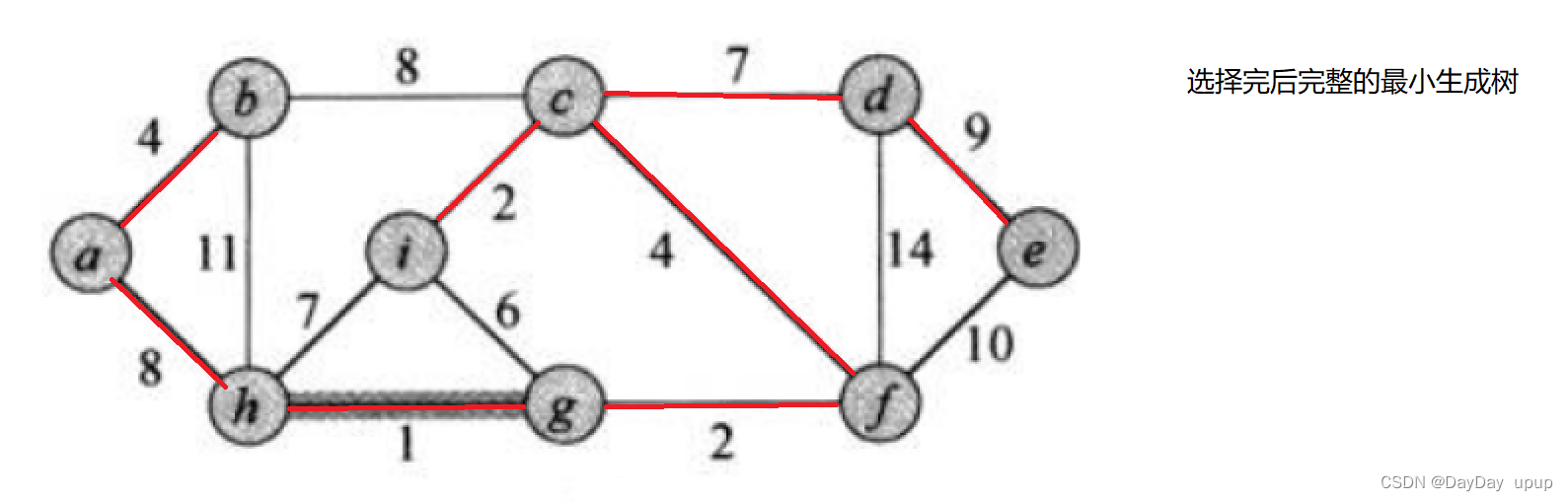
1. 利用优先级队列记录当前最小的边
2. 判断是否形成回路利用并查集

并查集

template<class W>
struct Edge
{
	Edge(int srci,int dsti,W w)
		:_srci(srci)
		,_dsti(dsti)
		,_w(w)
	{}
	bool operator>(const Edge& e) const 
	{
		return _w > e._w;
	}

	int _srci;
	int _dsti;
	W _w;
};
int Kruskal(self& minT)
{
	int n = _vertexs.size();
	minT._matrix.resize(n, vector<int>(n,MAX_W));

	minT._vertexs = _vertexs;
	minT._mapIndex = _mapIndex;
	unionFindSet ufs(n);
	priority_queue<Edge, vector<Edge>, greater<Edge>> pq;
	//将所有边入队列
	for (int i = 0; i < n; ++i)
	{
		for (int j = i+1; j < n; ++j)
		{
			if (_matrix[i][j] != MAX_W)
			{
				pq.push({ i,j,_matrix[i][j] });
			}
		}
	}
	int sz = 0;
	int mincount = 0;
	// 边不在一个集合，说明不会构成环，则添加到最小生成树
	while (!pq.empty() && sz < n - 1)
	{
		Edge tmp = pq.top();
		pq.pop();

		if (ufs.isSameRoot(tmp._dsti, tmp._srci) == false)
		{
			sz++;
			mincount += tmp._w;
			minT._matrix[tmp._dsti][tmp._srci] = tmp._w;

			ufs.gather(tmp._dsti, tmp._srci);
		}
	}
	if (sz != n - 1)
	{
		return -1;
	}
	return mincount;
}

void TestGraphMinTree()
{
const char* str = "abcdefghi";
Graph<char, int> g(str, strlen(str));
g.AddEdge('a', 'b', 4);
g.AddEdge('a', 'h', 8);
g.AddEdge('b', 'c', 8);
g.AddEdge('b', 'h', 11);
g.AddEdge('c', 'i', 2);
g.AddEdge('c', 'f', 4);
g.AddEdge('c', 'd', 7);
g.AddEdge('d', 'f', 14);
g.AddEdge('d', 'e', 9);
g.AddEdge('e', 'f', 10);
g.AddEdge('f', 'g', 2);
g.AddEdge('g', 'h', 1);
g.AddEdge('g', 'i', 6);
g.AddEdge('h', 'i', 7);
Graph<char, int> kminTree;
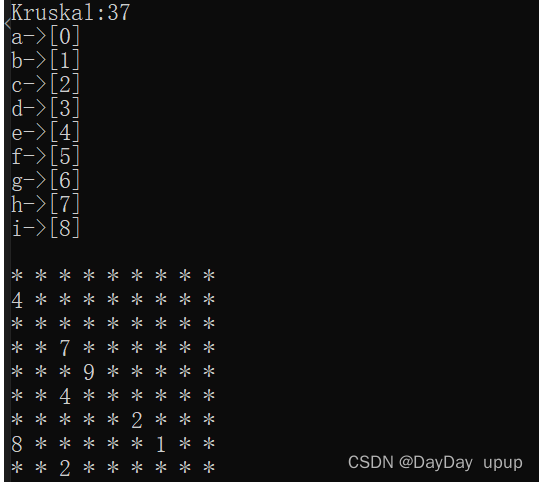
cout << "Kruskal:" << g.Kruskal(kminTree) << endl;
kminTree.print();
}

Prim算法

Prim与Kruskal算法类似区别在于
Kruskal算法:从整个图寻找最小的边去试
Prim算法:从某个节点出发，先找该节点相邻最小的边，每选取一个节点，将该节点所有的边入优先级队列，在选取最小的边去试

int Prim(self& minT,const V& start)
{
	int n = _vertexs.size();
	minT._matrix.resize(n, vector<int>(n, MAX_W));

	minT._vertexs = _vertexs;
	minT._mapIndex = _mapIndex;
	unionFindSet ufs(n);
	priority_queue<Edge, vector<Edge>, greater<Edge>> pq;
	int starti = findIndex(start);
	for (int i = 0; i < n; i++)
	{
		if (_matrix[starti][i] != MAX_W)
		{
			pq.push({ starti,i,_matrix[starti][i] });
		}
	}

	int sz = 0;
	int mincount = 0;


	while (!pq.empty() && sz < n - 1)
	{
		Edge tmp = pq.top();
		pq.pop();
		// 防止成环
		if (ufs.isSameRoot(tmp._dsti, tmp._srci) == false)
		{
			sz++;
			mincount += tmp._w;
			ufs.gather(tmp._dsti, tmp._srci);
			minT._matrix[tmp._dsti][tmp._srci] = tmp._w;
			// 	新入顶点的边入队列
			for (int i = 0; i < n; i++)
			{
				if (_matrix[tmp._dsti][i] != MAX_W)
				{
					pq.push({ tmp._dsti,i,_matrix[tmp._dsti][i] });
				}
			}
		}
	}
	if (sz != n - 1)
	{
		return -1;
	}

	return mincount;

}