Gauss消元的部分主元法和完全主元法(补充)

         本文主要是对下文的补充，而补充的主要内容就是如何直接求出(手动)部分主元法的P矩阵和L矩阵：

线性代数 --- Gauss消元的部分主元法和完全主元法_松下J27的博客-CSDN博客_高斯消元的主元是什么Gauss消元的部分主元法和完全主元法https://blog.csdn.net/daduzimama/article/details/124797212

         在我之前写的文章中，我留下了一个问题。那就是，如果在高斯消元的过程中使用了行交换（或者列交换），怎么才能像不选主元法那样直接写出标准的下三角L矩阵，以及对应的P矩阵，使得：PA=LU。后面，分别有两个热心的网友留言，并进行了答复。其中有一个网友的留言，我已经做了验证，正确的算法补充到了原文中。后来，又有一位网友留言，同时推荐了一本书（如下图）：

        这里面详细介绍了直接写出标准下三角矩阵L和置换矩阵P的办法。且，这本书里的方法和我前文中的方法不完全一样（可以说更好)，但也有相似之处，现在我就把数中的方法写出来。由于那本书中对矩阵的命名和我前文的命名有很大的不同，这里我依然沿用原书中的命名。

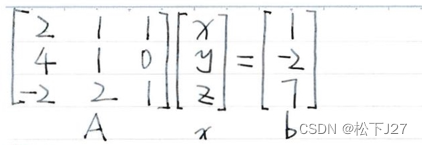
1，首先，依然沿用原来的例子：

        就不选主元法而言，这本书并没有使用基本消元矩阵E来记录高斯消元的过程。而是把主元下所有的元素的消元过程都放在一个矩阵中(或者说是用一个矩阵来记录一整列的消元过程)，书中用带有下标的L矩阵表示。

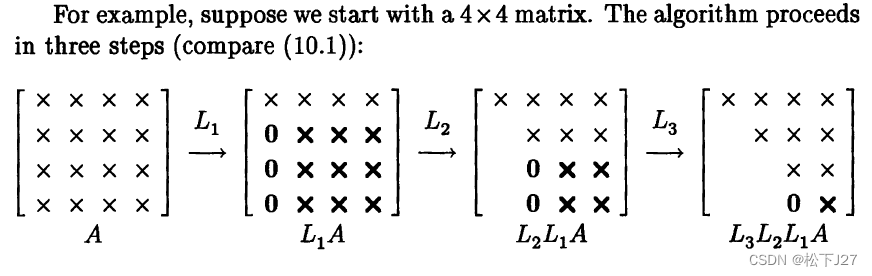
为了便于比较，我这里也把用消元矩阵E来表示的消元过程用和他类似的方式画下来了:

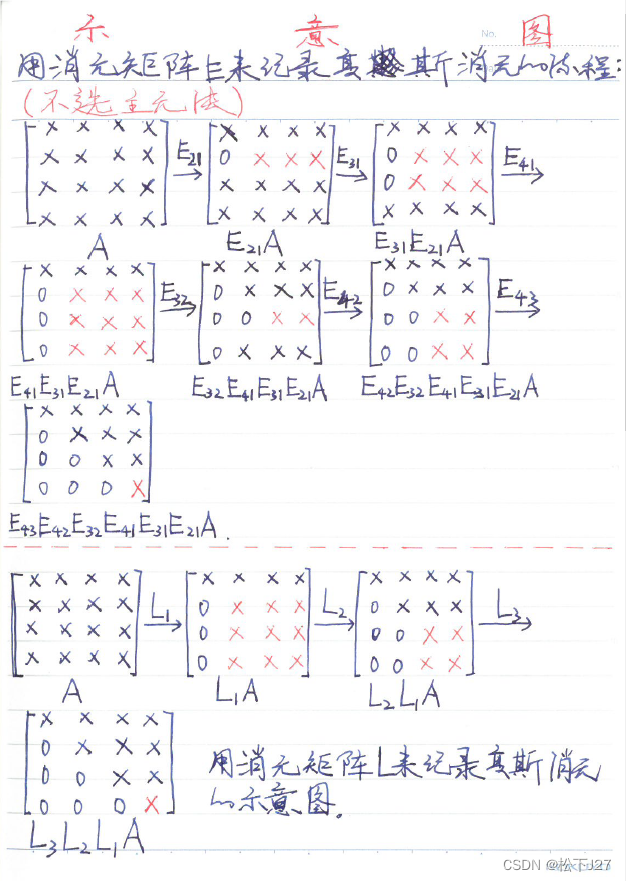
        前者是用来表示（或记录）消元的过程，而后者是用来表示消元的过程。而且，从上面的列子，我们可以看出对于4x4的矩阵而言：

2，他同样用到了基本消元矩阵的两个性质：

1，若要计算基本消元矩阵的逆，只需改变矩阵中第x行，第y列元素的符号即可。

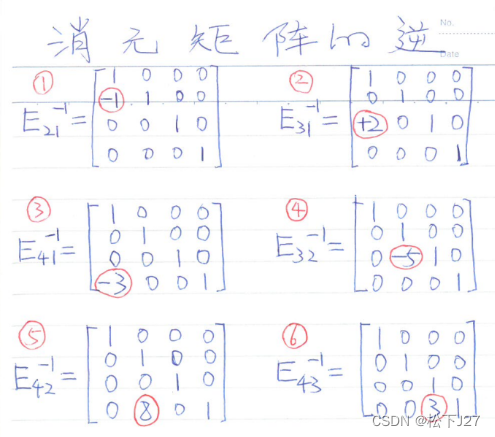
例如（这不是本文起始处Ax=b所对应的消元矩阵）：

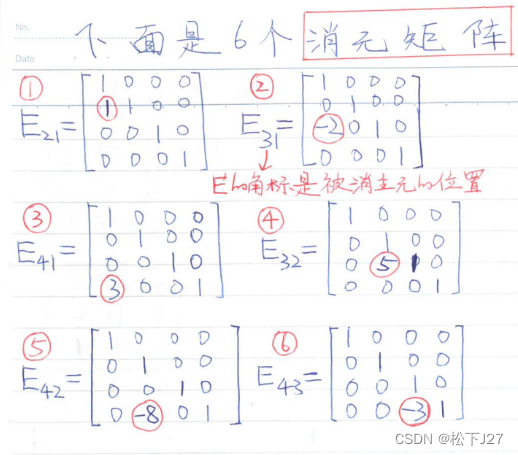
 6个消元矩阵的逆（只需改变对应元素的符号即可）

 2，要求多个的消元矩阵(例子中为消元矩阵的逆)的乘积，只需在单位矩阵I中，逐一填入对应位置的值即可。

例如：

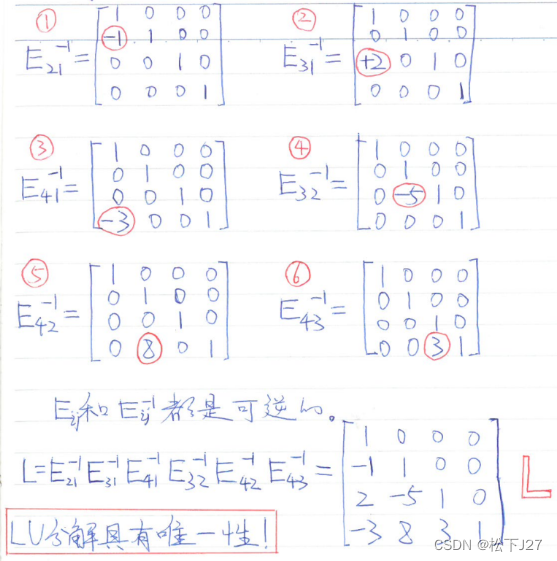
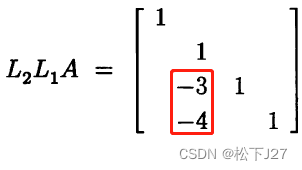
只不过，在这个作者的书中，他是以整列为单位操作的（即，以L矩阵为单位处理的)，如下：

并且，他把消元矩阵E的两个属性称为两个LUCK“ two stroke of luck”。

Luck 1(20.4)：等同于消元矩阵E的第一条属性，即，逆矩阵只需改变对应元素的符号即可:

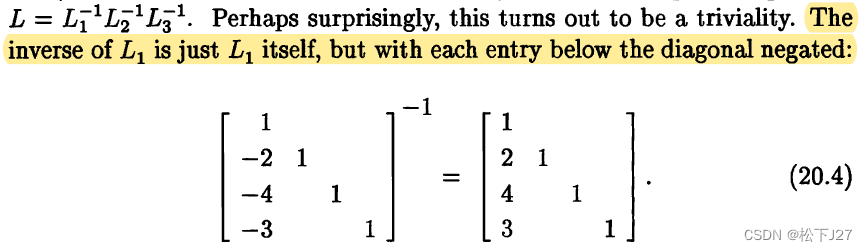
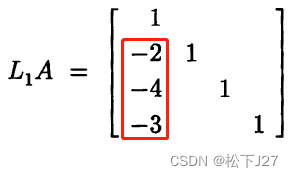
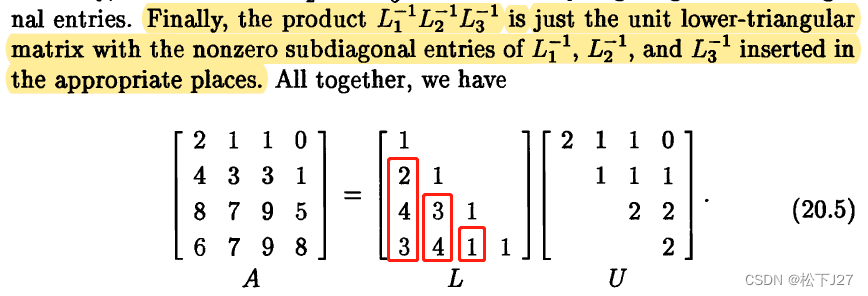
Luck 2(20.5)：等同于消元矩阵E的第二天属性，即，要求多个E的乘积，只需把E中的元素逐一填入单位矩阵I中对应的位置即可。

参考文献（鸣谢）：

 版权声明：所有的笔记，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27​