前言
这是时隔两年再参加比赛了,上次参加算法竞赛还是2020年在公司1024活动的时候。当时获得了二等奖(switch套装)和一个快题奖(小米行李箱)。

这次比赛获得了满分,也还不错。题目除了二维积水的问题(bfs+优先队列),其他难度都还好。

本次赛题
比赛地址:https://edu.csdn.net/contest/detail/30
奖惩名单:https://bbs.csdn.net/topics/611149502
T1 鬼画符门莲台争夺战
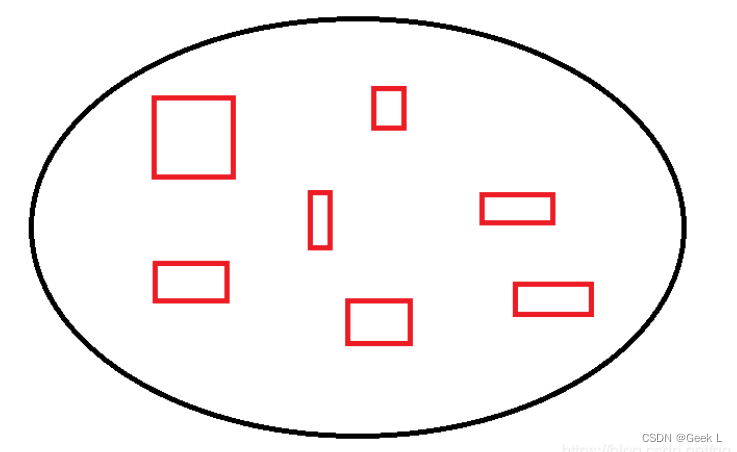
鬼画符门莲台争夺战! 虽然鬼画符门是一个三流门派但是近期为了改善宗门弟子质量。 特意引进了进化莲台。 部分精英 弟子会自己独占一块区域,或者几个精英弟子一块占领一块区域,他们占领的区域普通弟子不可以再占领,小艺作为普通 弟子想知道自己还能占领哪些地方。莲台区域以1开始,由小到大编号表示。
题解:用一个visi数组记录即可。
AC代码:
#include <iostream>
#include <string>
#include <sstream>
#include <vector>
using namespace std;
vector<int> solution(int n, int m, vector<vector<int>> vec) {
vector<int> result;
int visi[1005];
for (int i = 1; i <= m; i++) visi[i] = 0;
for (int i = 0; i < n; i++) {
for (int j = vec[i][0]; j <= vec[i][1]; j++)
visi[j] = 1;
}
for (int i = 1; i <= m; i++) if (visi[i] == 0)
result.push_back(i);
return result;
}
int main() {
int n;
int m;
vector<vector<int>> vec;
std::cin>>n;
std::cin>>m;
for (int i = 0; i < n; i++) {
int a, b;
cin >> a >> b;
vector<int> tmp;
tmp.push_back(a);
tmp.push_back(b);
vec.push_back(tmp);
}
vector<int> result = solution(n, m,vec);
int len = result.size();
cout << len << endl;
for (int i = 0; i < len; i++) {
cout << result[i] << " ";
}
cout << endl;
return 0;
}T2 津津的储蓄计划
津津的零花钱一直都是自己管理。每个月的月初妈妈给津津 300 元钱,津津会预算这个月的花销,并且总能做到实际花销 和预算的相同。 为了让津津学习如何储蓄,妈妈提出,津津可以随时把整百的钱存在她那里,到了年末她会加上 20% 还 给津津。
因此津津制定了一个储蓄计划:每个月的月初,在得到妈妈给的零花钱后,如果她预计到这个月的月末手中还会有多于 100 元或恰好 100 元,她就会把整百的钱存在妈妈那里,剩余的钱留在自己手中。 例如 11 月初津津手中还有 83 元, 妈妈给了津津 300 元。津津预计 11 月的花销是 180 元,那么她就会在妈妈那里存 200 元,自己留下 183 元。到了 11 月月末,津津手中会剩下 3 元钱。 津津发现这个储蓄计划的主要风险是,存在妈妈那里的钱在年末之前不能取出。有可能 在某个月的月初,津津手中的钱加上这个月妈妈给的钱,不够这个月的原定预算。如果出现这种情况,津津将不得不在这 个月省吃俭用,压缩预算。
现在请你根据2004年1月到12月每个月津津的预算,判断会不会出现这种情况。如果不会,计算到2004年年末,妈妈将 津津平常存的钱加上20%还给津津之后,津津手中会有多少钱。
题解:每次计算当前的剩余的钱,加上预算(+300),再减去该月的开销。如果小于0,则不够,输出这个月份对应的负数。如果>=0,就把100块整除的部分交给妈妈保管,余数部分自己剩下来接着用。
AC代码:
#include <iostream>
#include <string>
using namespace std;
int main() {
int t;
int d = 0, s = 0;
for (int i = 1; i <= 12; i++) {
cin >> t;
d += 300 - t;
if (d<0) {
cout << -i << endl;
return 0;
}
if (d/100) {
s+=d/100;
d=d%100;
}
}
cout << d+s*120 << endl;
return 0;
}T3 多边形的面积
给出一个简单多边形(没有缺口),它的边要么是垂直的,要么是水平的。要求计算多边形的面积。 多边形被放置在一个 X- Y 的卡笛尔平面上,它所有的边都平行于两条坐标轴之一。然后按逆时针方向给出各顶点的坐标值。所有的坐标值都是整 数(因此多边形的面积也为整数)。
题解:典型的凸包计算,连排序都给咱们排好了,直接用公式即可。
AC代码:
#include <iostream>
#include <string>
#include <sstream>
#include <vector>
using namespace std;
int main() {
int n;
cin>>n;
vector<vector<int>> vec;
for (int i = 0; i < n; i++) {
vector<int> tmp;
int x;
cin >> x;
tmp.push_back(x);
cin >> x;
tmp.push_back(x);
vec.push_back(tmp);
}
vector<int> tmp = vec[0];
vec.push_back(tmp);
int res = 0;
for (int i = 0; i < n; i++) {
res += vec[i][0] * vec[i+1][1] - vec[i+1][0] * vec[i][1];
//cout << i << endl;
//cout << "res: " << res << endl;
}
if (res < 0) res = 0 - res;
cout << res / 2 << endl;
return 0;
}T4 小桥流水人家
在n*m的地图上,存在一个喷水点,如果相邻的位置低于有水的地方,水就能流到相邻的某位置(即该格子需要其上下左 右的格子海拔都比自身高的封闭图形才可以积水)。 已知各个格子的海拔高度,求积水的最大覆盖个格子数。
题解:这个题目是leetcode407 接雨水2。我在之前的博客中有讲解到:lintcode 矩阵问题(最全的面试矩阵问题)_果7的博客-CSDN博客
如果一个位置能找到往外流出的路径,那么这个位置不能接水。
我们可以使用BFS+优先队列来解决这个问题。
1.首先把边界的点加入到队列中,每次出队选择高度最低的出队。
2.记录之前的最大值,如果当前值比最大值小,表示可以装水。
【如果可以漫出,那么之前的最大值一定<=当前值】
【队列里的元素和之前最大的元素是边界,都>=之前的最大值】
PS:使用tuple会超时 (换成了pair 压缩行和列)
AC代码:
#include <iostream>
#include <string>
#include <sstream>
#include <vector>
#include <queue>
using namespace std;
int main() {
int n, m;
vector<vector<int>> vec;
cin >> n >> m;
for (int i = 0; i < n; i++) {
vector<int> tmp;
int x;
for (int j = 0; j < m; j++) {
cin >> x;
tmp.push_back(x);
}
vec.push_back(tmp);
}
int dir[4][2] = {{-1,0},{1,-0},{0,1},{0,-1}};
if (n < 3 || m < 3) {
cout << 0 << endl;
return 0;
}
vector<vector<bool>> visi(n, vector<bool>(m, false));
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (i == 0 || i == n-1 || j==0 || j == m-1) {
visi[i][j] = true;
q.push(make_pair(vec[i][j], i*m+j));
}
}
}
int res = 0, max_h = 0;
while(!q.empty()) {
pair<int, int> t = q.top();
q.pop();
int x = t.second / m, y = t.second % m, h = t.first;
res += max(0, max_h-h);
max_h = max(max_h, h);
for (int i = 0; i < 4; i++) {
int cx = x + dir[i][0], cy = y + dir[i][1];
if (cx>=0&&cx<n&&cy>=0&&cy<m&&!visi[cx][cy]) {
visi[cx][cy] = true;
q.push(make_pair(vec[cx][cy], cx*m+cy));
}
}
}
cout << res << endl;
return 0;
}