文章目录
- 1、数列的极限
- 1.1、数列极限的定义
- 1.2、为什么收敛数列极限是唯一的?
- 1.3、为什么收敛数列是有界的?
- 1.4、数列极限的保号性
- 1.4.1、极限保数列值
- 1.4.2、数列值保极限值
- 1.5、收敛数列与其子列之间的关系
- 2、函数极限概念
- 2.1、函数极限的定义
- 2.1.1、自变量趋于有限值时函数的极限
- 2.1.1.1、左极限与右极限
- 2.1.2、自变量趋于无穷大时函数的极限
- 2.2、函数极限的性质
- 2.2.1、唯一性
- 2.2.2、局部有界性
- 2.2.3、局部保号性
- 2.2.3.1、极限保函数
- 2.2.3.2、函数保极限
- 2.2.4、函数极限与数列极限的关系
- 3、无穷大与无穷小
- 3.1、无穷小
- 3.1.1、定义
- 3.1.2、几何意义
- 3.1.3、无穷小的比较
- 3.1.4、常用等价无穷小代换
- 3.2、无穷大
- 3.2.1、定义
- 3.2.2、正无穷大与负无穷大
- 3.2.3、几何意义
- 3.3、无穷大与无穷小的关系
- 4、极限运算法则
- 4.1、基本定理
- 4.2、极限的四则运算
- 4.3、极限的比较大小
- 4.4、复合函数的极限
- 极限(下)超链接
1、数列的极限
lim n → ∞ x n = a \lim_{n \to ∞}x_n = a n→∞limxn=a
1.1、数列极限的定义
定义1:
∀
\forall
∀
ϵ
\epsilon
ϵ > 0,
∃
\exists
∃N > 0 , 当n > N 时 , 恒有 |
x
n
x_n
xn - a|<
ϵ
\epsilon
ϵ.
N的作用: N是用来描述的
n
→
∞
{n \to ∞}
n→∞这个过程的,由于N的存在性,所以N是一个有限数**,而n是一个趋近于无穷的数,则n在趋近于无穷这个过程中一定超过N
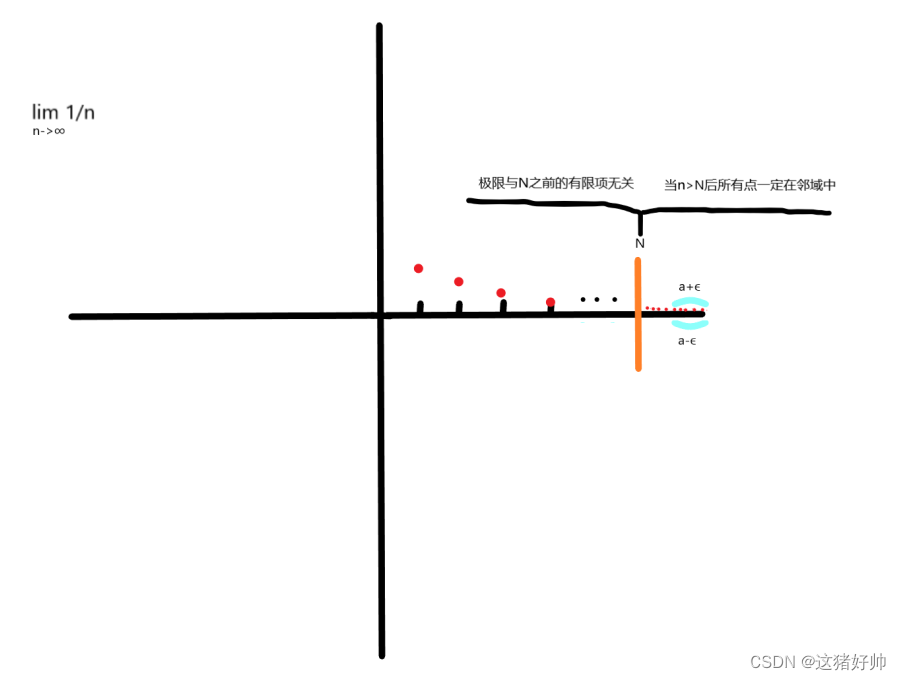
于是我们把这个式子通俗解释即为:
存在有限数N,存在一个邻域U(a, ϵ \epsilon ϵ),当n > N后的无限项都落在这个邻域中,则a为原数列的极限
注意:由于
ϵ
\epsilon
ϵ是变化的,所以这个邻域可以变成要多小有多小的邻域
如图:
1.2、为什么收敛数列极限是唯一的?
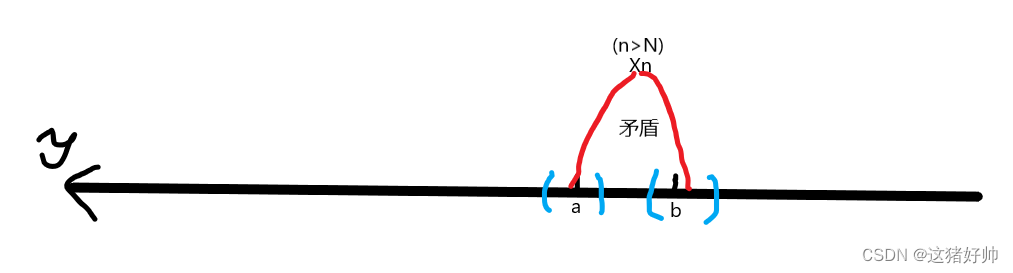
我们先通过几何来看
如果收敛数列的极限为a和b 假设a >b
我们取两个邻域U1(a,
ϵ
\epsilon
ϵ),U2(b,
ϵ
\epsilon
ϵ),且U1和U2没有重叠部分
根据数列极限的定义
当n>N时,每一项既要落在U1也要落在U2,但是数列的一项只能有一个值,于是就发生了冲突
如图:
数学证明:
取
ϵ
\epsilon
ϵ =
a
−
b
2
\frac{a-b}{2}
2a−b
∃
\exists
∃N > 0
当n > N时满足:
①|
x
n
−
a
x_n-a
xn−a| <
a
−
b
2
\frac{a-b}{2}
2a−b
②|
x
n
x_n
xn - b| <
a
−
b
2
\frac{a-b}{2}
2a−b
① =
b
−
a
2
+
a
\frac{b-a}{2}+a
2b−a+a <
x
n
x_n
xn <
a
−
b
2
+
a
\frac{a-b}{2}+a
2a−b+a
② =
b
−
a
2
+
b
\frac{b-a}{2}+b
2b−a+b <
x
n
x_n
xn <
a
−
b
2
+
b
\frac{a-b}{2}+b
2a−b+b
化简上式得:
x
n
x_n
xn >
b
+
a
2
\frac{b+a}{2}
2b+a 且
x
n
x_n
xn <
b
+
a
2
\frac{b+a}{2}
2b+a
证毕
1.3、为什么收敛数列是有界的?
lim
n
→
∞
x
n
=
a
\lim_{n \to ∞}x_n = a
n→∞limxn=a
首先,还是从几何上来看,我们根据定义:
收敛数列当n > N 时,会全部落在一个邻域U(a,
ϵ
\epsilon
ϵ)
说明N之后的无穷项 a -
ϵ
\epsilon
ϵ <
x
n
x_n
xn < a +
ϵ
\epsilon
ϵ ,而我们只需要考虑N之前的,及邻域端点的情况
如图:

数学证明:
由
∀
\forall
∀
ϵ
\epsilon
ϵ > 0,
∃
\exists
∃N > 0 , 当n > N 时 , 恒有 |
x
n
x_n
xn - a|<
ϵ
\epsilon
ϵ
得当n > N 时恒有界
令M =max{
∣
x
1
∣
,
∣
x
2
∣
,
∣
x
3
∣
,
.
.
.
,
∣
x
N
∣
,
∣
a
+
ϵ
∣
,
∣
a
−
ϵ
∣
|x_1|,|x_2|,|x_3|,...,|x_N|,|a+ϵ|,|a-ϵ|
∣x1∣,∣x2∣,∣x3∣,...,∣xN∣,∣a+ϵ∣,∣a−ϵ∣}
证得:
lim
n
→
∞
x
n
<
M
\lim_{n \to ∞}x_n <M
limn→∞xn<M
注意:
1、有界数列不一定收敛,例如
x
n
=
(
−
1
)
n
−
1
x_n = (-1)^{n-1}
xn=(−1)n−1
2、由于收敛一定有界,所以无界一定发散,但发散不一定无界,例如
x
n
=
(
−
1
)
n
−
1
x_n = (-1)^{n-1}
xn=(−1)n−1
1.4、数列极限的保号性
1.4.1、极限保数列值
定义:若 lim n → ∞ x n = a \lim_{n \to ∞}x_n = a limn→∞xn=a,且 a > 0 a > 0 a>0(或 a < 0 a < 0 a<0),则 ∃ N \exists N ∃N,当 n > N n > N n>N时,都有 x n > 0 x_n > 0 xn>0(或 x n < 0 x_n < 0 xn<0)
我们还是从几何上来看看(我们证明a > 0时一定有
x
n
>
0
x_n > 0
xn>0,反之证明方法一样):
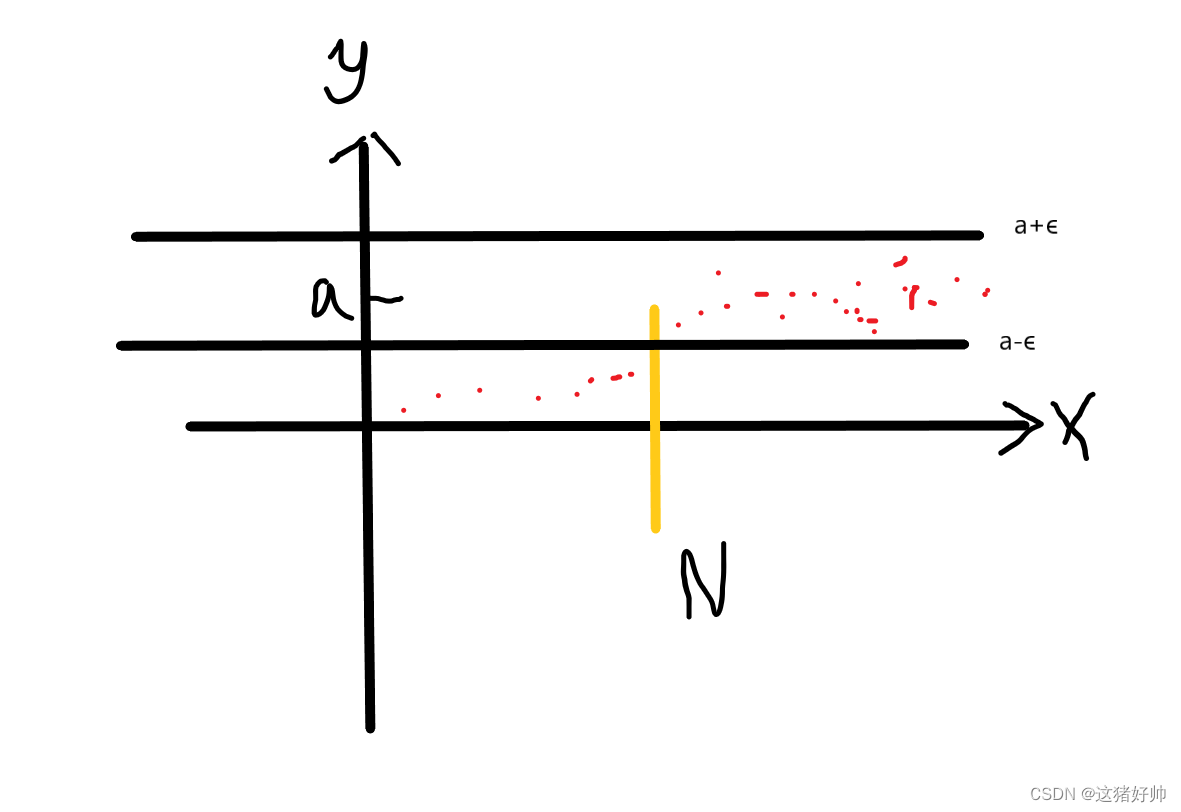
由图中我们可以看到当第N项之后的每一项都落在了U(a,ϵ)
∵a≠0,a>0
所以无论a取多小,只要a - ϵ > 0即可满足
数学证明:
取
ϵ
=
a
2
ϵ = \frac{a}{2}
ϵ=2a
由
∀
\forall
∀
ϵ
\epsilon
ϵ > 0,
∃
\exists
∃N > 0 , 当n > N 时 , 恒有 |
x
n
x_n
xn - a|<
ϵ
\epsilon
ϵ
展开得
a
−
ϵ
<
x
n
<
a
+
ϵ
a - ϵ < x_n < a + ϵ
a−ϵ<xn<a+ϵ
解得
x
n
>
a
2
(
a
>
0
)
x_n > \frac{a}{2}(a>0)
xn>2a(a>0)
证毕
此时我们取极限值保数列值的逆否命题,即为数列值保极限值
1.4.2、数列值保极限值
推论:如果 ∃ N > 0 \exist N>0 ∃N>0,当 n > N n >N n>N时, x n ≤ 0 ( 或 x n ≥ 0 ) x_n\leq0(或x_n\geq0 ) xn≤0(或xn≥0)则 a ≥ 0 ( 或 a ≤ 0 ) a\geq0(或a\leq 0) a≥0(或a≤0)
这里的
a
≥
0
a \geq 0
a≥0
原因是当某一个数列的极限为0时,它的极限的定义是在这一点上的一个邻域
也就是说,虽然极限值是0,但数列值可以取到>0的部分
(例如
x
n
=
1
n
x_n = \frac{1}{n}
xn=n1数列值恒>0,但这个数列的极限是0)
1.5、收敛数列与其子列之间的关系
lim
n
→
∞
x
n
=
a
⇚
⇛
lim
k
→
∞
x
2
k
=
lim
k
→
∞
x
2
k
−
1
\lim_{n \to ∞}x_n = a \Lleftarrow\Rrightarrow\lim_{k \to ∞}x_{2k} = \lim_{k \to ∞}x_{2k-1}
limn→∞xn=a⇚⇛limk→∞x2k=limk→∞x2k−1
x
2
k
x_{2k}
x2k为偶数列
x
2
k
−
1
x_{2k-1}
x2k−1为奇数列
注意:如果子列的极限不相等,仅仅是存在的话无法推出收敛数列的极限(例如 x n = ( − 1 ) n − 1 x_n = (-1)^{n-1} xn=(−1)n−1)**
2、函数极限概念
2.1、函数极限的定义
2.1.1、自变量趋于有限值时函数的极限
定义:设函数f(x)在点
x
0
x_0
x0的某个去心邻域有定义,若
∀
ϵ
>
0
,
∃
δ
>
0
∀ϵ>0,∃\delta>0
∀ϵ>0,∃δ>0,
0
<
∣
x
−
x
0
∣
<
δ
0<|x-x_0|<\delta
0<∣x−x0∣<δ时,恒有
∣
f
(
x
)
−
A
∣
<
ϵ
|f(x)-A|<\epsilon
∣f(x)−A∣<ϵ
记作
lim
x
→
x
0
f
(
x
)
=
A
\lim_{x \to x_0}f(x) = A
x→x0limf(x)=A
注意:
1、
ϵ
\epsilon
ϵ是任意的,它的任意性也就刻画了函数值
f
(
x
)
f(x)
f(x)与极限值A要多接近有多接近
2、由定义
∣
x
−
x
0
∣
>
0
|x-x_0|>0
∣x−x0∣>0就说明
x
≠
x
0
x≠x_0
x=x0
3、
δ
\delta
δ是用来刻画
x
→
x
0
x \to x_0
x→x0这个过程的一个变量
如图(
lim
x
→
x
0
y
=
x
2
,
x
0
=
2
\lim_{x \to x_0}y = x^2,x_0 =2
limx→x0y=x2,x0=2):

我们可以看到,当
x
x
x落在
U
˚
(
x
0
,
δ
)
\mathring{U}(x_0, \delta)
U˚(x0,δ)时恒有
f
(
x
)
f(x)
f(x)落在
U
(
A
,
ϵ
)
{U}(A, \epsilon)
U(A,ϵ)(无论
ϵ
\epsilon
ϵ有多小)
通俗点说:说明只要
f
(
x
)
f(x)
f(x)以A为极限,就一定可以在x轴上找到一个邻域
U
˚
(
x
0
,
δ
)
\mathring U(x_0,\delta)
U˚(x0,δ),当x的取值落在这个邻域后它对应的
f
(
x
)
f(x)
f(x)的函数值一定落在
U
(
A
,
ϵ
)
U(A,\epsilon)
U(A,ϵ)中。
2.1.1.1、左极限与右极限
左极限:若
∀
ϵ
>
0
,
∃
δ
>
0
∀ϵ>0,∃\delta>0
∀ϵ>0,∃δ>0,
0
<
x
0
−
x
<
δ
0<x_0-x<\delta
0<x0−x<δ时,恒有
∣
f
(
x
)
−
A
∣
<
ϵ
|f(x)-A|<\epsilon
∣f(x)−A∣<ϵ
记作
lim
x
→
x
0
−
f
(
x
)
=
f
(
x
0
−
)
=
f
(
x
0
−
0
)
\lim_{x \to x_0^{-}}f(x)=f(x_0^-)=f(x_0 -0)
x→x0−limf(x)=f(x0−)=f(x0−0)
右极限:若
∀
ϵ
>
0
,
∃
δ
>
0
∀ϵ>0,∃\delta>0
∀ϵ>0,∃δ>0,
0
<
x
−
x
0
<
δ
0<x-x_0<\delta
0<x−x0<δ时,恒有
∣
f
(
x
)
−
A
∣
<
ϵ
|f(x)-A|<\epsilon
∣f(x)−A∣<ϵ
记作
lim
x
→
x
0
+
f
(
x
)
=
f
(
x
0
+
)
=
f
(
x
0
+
0
)
\lim_{x \to x_0^{+}}f(x) = f(x_0^+)=f(x_0 +0)
x→x0+limf(x)=f(x0+)=f(x0+0)
即:在
U
˚
(
x
0
,
δ
)
\mathring U(x_0,\delta)
U˚(x0,δ)中,以
x
=
x
0
x = x_0
x=x0为界限,左边的即为左极限,右边的即为右极限
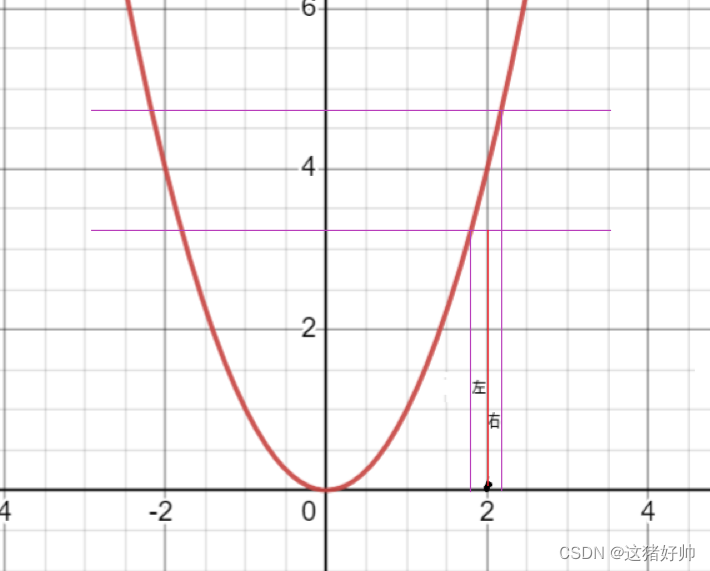
左右极限与极限得关系:如图我们很容易看出来,如果极限要存在的话,那么左右极限就一定要存在,并且左右极限要相等,反之左右极限存在并且相等的话,极限值也一定存在
lim
x
→
x
0
f
(
x
)
⇚
⇛
lim
x
→
x
0
+
f
(
x
)
=
lim
x
→
x
0
−
f
(
x
)
=
A
\lim_{x \to x_0}f(x) \Lleftarrow\Rrightarrow\lim_{x \to x_0^+}f(x) =\lim_{x \to x_0^-}f(x)=A
limx→x0f(x)⇚⇛limx→x0+f(x)=limx→x0−f(x)=A
注意:极限讨论的
x
x
x所属邻域 是去心的,所以极限值与函数在去心点
x
0
x_0
x0的值无关
2.1.2、自变量趋于无穷大时函数的极限
定义:
∀
ϵ
>
0
,
∃
X
>
0
∀ϵ>0,∃X>0
∀ϵ>0,∃X>0,当
∣
x
∣
>
X
|x| > X
∣x∣>X时,恒有
∣
f
(
x
)
−
A
∣
<
ϵ
|f(x)-A|<\epsilon
∣f(x)−A∣<ϵ
记作
lim
x
→
∞
f
(
x
)
=
A
\lim_{x \to ∞}f(x) = A
x→∞limf(x)=A
我们把
∣
f
(
x
)
−
A
∣
|f(x)-A|
∣f(x)−A∣展开后:
A
−
ϵ
<
f
(
x
)
<
A
+
ϵ
A-\epsilon<f(x) < A + \epsilon
A−ϵ<f(x)<A+ϵ
同样的,这里得
ϵ
\epsilon
ϵ是表示当x满足条件时,那么
f
(
x
)
f(x)
f(x)与极限值A之间要多接近有多接近
即当
∣
x
∣
>
X
|x|>X
∣x∣>X时,函数值一定落在去心邻域
U
(
A
,
ϵ
)
U(A,\epsilon)
U(A,ϵ)
如图(x>0部分,x<0时同理):

几何意义:由上图我们也可以看出来,当
x
→
∞
x \to ∞
x→∞时,y = f(x)是以极限值y = A为水平渐近线来逼近得
2.1.2.1 、 + ∞ 与 − ∞ 2.1.2.1、+∞与-∞ 2.1.2.1、+∞与−∞
当
x
→
+
∞
x \to +∞
x→+∞时的定义:定义:
∀
ϵ
>
0
,
∃
X
>
0
∀ϵ>0,∃X>0
∀ϵ>0,∃X>0,当
x
>
X
x > X
x>X时,恒有
∣
f
(
x
)
−
A
∣
<
ϵ
|f(x)-A|<\epsilon
∣f(x)−A∣<ϵ
当
x
→
−
∞
x \to -∞
x→−∞时的定义:定义:
∀
ϵ
>
0
,
∃
X
>
0
∀ϵ>0,∃X>0
∀ϵ>0,∃X>0,当
x
<
−
X
x < -X
x<−X时,恒有
∣
f
(
x
)
−
A
∣
<
ϵ
|f(x)-A|<\epsilon
∣f(x)−A∣<ϵ
定义我们能看出: lim x − > ∞ f ( x ) ⇚ ⇛ lim x → + ∞ f ( x ) = lim x → − ∞ f ( x ) = A \lim_{x->∞}f(x)\Lleftarrow\Rrightarrow\lim_{x \to +∞}f(x) = \lim_{x \to -∞}f(x) =A limx−>∞f(x)⇚⇛limx→+∞f(x)=limx→−∞f(x)=A
2.2、函数极限的性质
2.2.1、唯一性
函数极限是唯一的
原因是如果有两个极限,A和B,那么总会存在一个X当
∣
x
∣
>
X
|x|>X
∣x∣>X时无法同时包含A和B,也就是无法在同一个邻域中同时取得A和B
【图参考数列极限的唯一性】
【证明函数极限唯一性】
不妨令
lim
x
→
x
0
f
(
x
)
=
A
\lim_{x \to x_0}f(x) = A
limx→x0f(x)=A,
lim
x
→
x
0
f
(
x
)
=
B
(
A
>
B
)
\lim_{x \to x_0}f(x) = B(A>B)
limx→x0f(x)=B(A>B)
令
ϵ
=
A
−
B
2
\epsilon = \frac{A-B}{2}
ϵ=2A−B
证明:即
∃
δ
>
0
∃\delta>0
∃δ>0,
0
<
∣
x
−
x
0
∣
<
δ
0<|x-x_0|<\delta
0<∣x−x0∣<δ时,恒有
∣
f
(
x
)
−
A
∣
<
ϵ
|f(x)-A| <\epsilon
∣f(x)−A∣<ϵ
又
∃
δ
>
0
∃\delta>0
∃δ>0,
0
<
∣
x
−
x
0
∣
<
δ
0<|x-x_0|<\delta
0<∣x−x0∣<δ时,恒有
∣
f
(
x
)
−
B
∣
<
ϵ
|f(x)-B|<\epsilon
∣f(x)−B∣<ϵ
由定义得:
A
−
A
−
B
2
<
f
(
x
)
<
A
+
A
−
B
2
化简
A
+
B
2
<
f
(
x
)
<
3
A
−
B
2
A-\frac{A-B}{2}<f(x) < A+\frac{A-B}{2}化简\frac{A+B}{2} <f(x)<\frac{3A-B}{2}
A−2A−B<f(x)<A+2A−B化简2A+B<f(x)<23A−B
B
−
A
−
B
2
<
f
(
x
)
<
B
+
A
−
B
2
化简
2
B
−
A
2
<
f
(
x
)
<
A
+
B
2
B-\frac{A-B}{2}<f(x) < B+\frac{A-B}{2}化简\frac{2B-A}{2} <f(x)<\frac{A+B}{2}
B−2A−B<f(x)<B+2A−B化简22B−A<f(x)<2A+B
得:
A
+
B
2
>
f
(
x
)
>
A
+
B
2
\frac{A+B}{2}>f(x)>\frac{A+B}{2}
2A+B>f(x)>2A+B
∴
f
(
x
)
f(x)
f(x)不存在
证毕
2.2.2、局部有界性
定义:
∃
M
>
0
与
δ
>
0
\exist M>0与\delta>0
∃M>0与δ>0,使得
∀
x
∈
U
˚
(
x
0
,
δ
)
\forall x\in \mathring U(x_0,\delta)
∀x∈U˚(x0,δ)有
∣
f
(
x
)
∣
≤
M
|f(x)|\leq M
∣f(x)∣≤M
这个定义说明了,只要一个函数在某一点上有极限,则在这个点得去心邻域有界,去心是因为极限值与在这一点上得函数值无关,局部是因为极限得定义规定了,极限至于在这一点上得去心邻域有关,跟其他无关
注意:局部有界无法推出函数在这一点上有极限
(例如:
lim
x
→
0
s
i
n
(
1
x
)
\lim_{x \to 0}sin(\frac{1}{x})
limx→0sin(x1))
2.2.3、局部保号性
2.2.3.1、极限保函数
定义:如果 A > 0 ( 或 A < 0 ) A>0(或A<0) A>0(或A<0),则存在 δ > 0 \delta>0 δ>0,当 x ∈ U ˚ ( x 0 , δ ) x\in\mathring U(x_0,\delta) x∈U˚(x0,δ)时, f ( x ) > 0 ( 或 f ( x ) < 0 ) f(x)>0(或f(x)<0) f(x)>0(或f(x)<0)
这个与数列极限很像,唯一的不同就是数列保的是
n
>
N
n>N
n>N后的无穷项,而函数保的是以取得极限值的
x
0
x_0
x0点为中心,的一个小的去心邻域
而数列极限可以通过极限值保数列值,也能通过数列值保极限值,同样的函数也是如此
推论:如果
A
≠
0
A≠0
A=0,则存在
δ
>
0
\delta>0
δ>0,当
x
∈
U
˚
(
x
0
,
δ
)
x \in\mathring U(x_0,\delta)
x∈U˚(x0,δ)时,
∣
f
(
x
)
∣
>
∣
A
∣
2
|f(x)|>\frac{|A|}{2}
∣f(x)∣>2∣A∣
我们先从A >0来看:
∵
A
>
0
∵A>0
∵A>0,∴当
x
∈
U
˚
(
x
0
,
δ
)
x \in\mathring U(x_0,\delta)
x∈U˚(x0,δ)时
f
(
x
)
>
0
f(x)>0
f(x)>0
上述推论就变为:
如果
A
>
0
A>0
A>0,则存在
δ
>
0
\delta>0
δ>0,当
x
∈
U
˚
(
x
0
,
δ
)
x \in\mathring U(x_0,\delta)
x∈U˚(x0,δ)时,
f
(
x
)
>
A
2
f(x)>\frac{A}{2}
f(x)>2A
根据极限得定义:我们取
ϵ
=
A
2
\epsilon =\frac{A}{2}
ϵ=2A
∃
δ
>
0
,
当
x
∈
U
˚
(
A
,
δ
)
时
\exist\delta>0,当x\in\mathring U(A,\delta)时
∃δ>0,当x∈U˚(A,δ)时,有
f
(
x
)
>
A
−
A
2
=
A
2
f(x)>A-\frac{A}{2}=\frac{A}{2}
f(x)>A−2A=2A
证毕
如果A<0,证明方法也是类似使用保号性进行证明
2.2.3.2、函数保极限
推论:如果
∃
δ
>
0
\exist \delta>0
∃δ>0当
x
∈
U
˚
(
x
0
,
δ
)
x \in\mathring U(x_0,\delta)
x∈U˚(x0,δ)时,
f
(
x
)
≥
0
(
或
f
(
x
)
≤
0
)
f(x)\geq0(或f(x)\leq0)
f(x)≥0(或f(x)≤0),那么
A
≥
0
(
或
A
≤
0
)
A\geq0(或A\leq0)
A≥0(或A≤0)
这里也是跟数列极限一样的,A需要可以取到0这个点,原因是讨论极限讨论的是一个去心邻域,则函数值>0的时候只要符合
x
∈
U
˚
(
x
0
,
δ
)
x \in \mathring U(x_0,\delta)
x∈U˚(x0,δ)这个条件即可
例如(
lim
x
→
+
∞
y
=
1
x
\lim_{x \to +∞}y=\frac{1}{x}
limx→+∞y=x1)虽然恒
≥
0
\geq0
≥0但它的极限值为0
2.2.4、函数极限与数列极限的关系
若
lim
x
→
x
0
f
(
x
)
=
A
,
且
l
i
m
n
→
∞
x
n
=
x
0
,
x
n
≠
x
0
,
则
lim
n
→
∞
f
(
x
n
)
=
A
\lim_{x \to x_0}f(x) = A,且lim_{n \to ∞}x_n = x_0,x_n≠x_0,则\lim_{n \to ∞}f(x_n)=A
limx→x0f(x)=A,且limn→∞xn=x0,xn=x0,则limn→∞f(xn)=A
用通俗点得话说就是,函数极限是A,数列极限是
x
0
x_0
x0,那么这个函数与数列复合而成的新数列就以A为极限
注意:这里得
x
n
≠
x
0
x_n ≠ x_0
xn=x0不能去掉
原因是前面得函数
x
→
x
0
,
但
x
≠
x
0
x\to x_0,但x ≠x_0
x→x0,但x=x0,也就是说哪怕函数在
x
0
x_0
x0点无定义,它照样可以有极限,那么数列极限也只能
→
x
0
,
而
≠
x
0
\to x_0,而≠x_0
→x0,而=x0
3、无穷大与无穷小
3.1、无穷小
3.1.1、定义
定义:如果函数 f ( x ) f(x) f(x)当 x → x 0 ( 或 x → ∞ ) x \to x_0(或x \to ∞) x→x0(或x→∞)时的极限为零,则称 f ( x ) f(x) f(x)为 x → x 0 ( 或 x → ∞ ) x \to x_0(或x \to ∞) x→x0(或x→∞)时的无穷小量
通俗的来说,只要函数极限值为0,则
f
(
x
)
f(x)
f(x)即为无穷小
例1:
lim
x
→
0
s
i
n
x
=
0
\lim_{x \to 0}sinx=0
x→0limsinx=0
即:sinx是
x
→
0
x \to 0
x→0时的无穷小量
例2:
lim
x
→
∞
1
x
=
0
\lim_{x \to ∞}\frac{1}{x}=0
x→∞limx1=0即:
1
x
\frac{1}{x}
x1是
x
→
∞
x \to ∞
x→∞时的无穷小量
例3:
lim
x
→
0
−
e
1
x
=
0
\lim_{x \to 0^-}e^{\frac{1}{x}}=0
x→0−limex1=0即:
e
1
x
e^{\frac{1}{x}}
ex1是
x
→
0
−
x \to 0^-
x→0−时的无穷小量
注意:
1、无穷小是个变量,不能与很小的数混淆(如:0.000…1不能叫做无穷小量)
2、零是可以作为无穷小的唯一的数
lim
x
→
x
0
f
(
x
)
=
A
\lim_{x \to x_0}f(x)=A
limx→x0f(x)=A
令
a
(
x
)
=
f
(
x
)
−
A
a(x) = f(x)-A
a(x)=f(x)−A
即可得出以下定理
定理:
lim
f
(
x
)
=
A
⇚
⇛
f
(
x
)
=
A
+
a
(
x
)
\lim f(x)=A\Lleftarrow\Rrightarrow f(x)=A+a(x)
limf(x)=A⇚⇛f(x)=A+a(x)
其中
lim
a
(
x
)
=
0
\lim a(x) = 0
lima(x)=0
这个定理的意思是只要是一个函数以A为极限,那么一定能写成一个常数
A
+
无穷小量
A+无穷小量
A+无穷小量
其中,这个无穷小量表示的就是
f
(
x
)
f(x)
f(x)在这一点上的函数值与极限值A之间距离
3.1.2、几何意义
我们以
lim
x
→
∞
1
x
=
0
\lim_{x \to ∞}\frac{1}{x}=0
limx→∞x1=0为例,如图为
f
(
x
)
=
1
x
f(x)=\frac{1}{x}
f(x)=x1
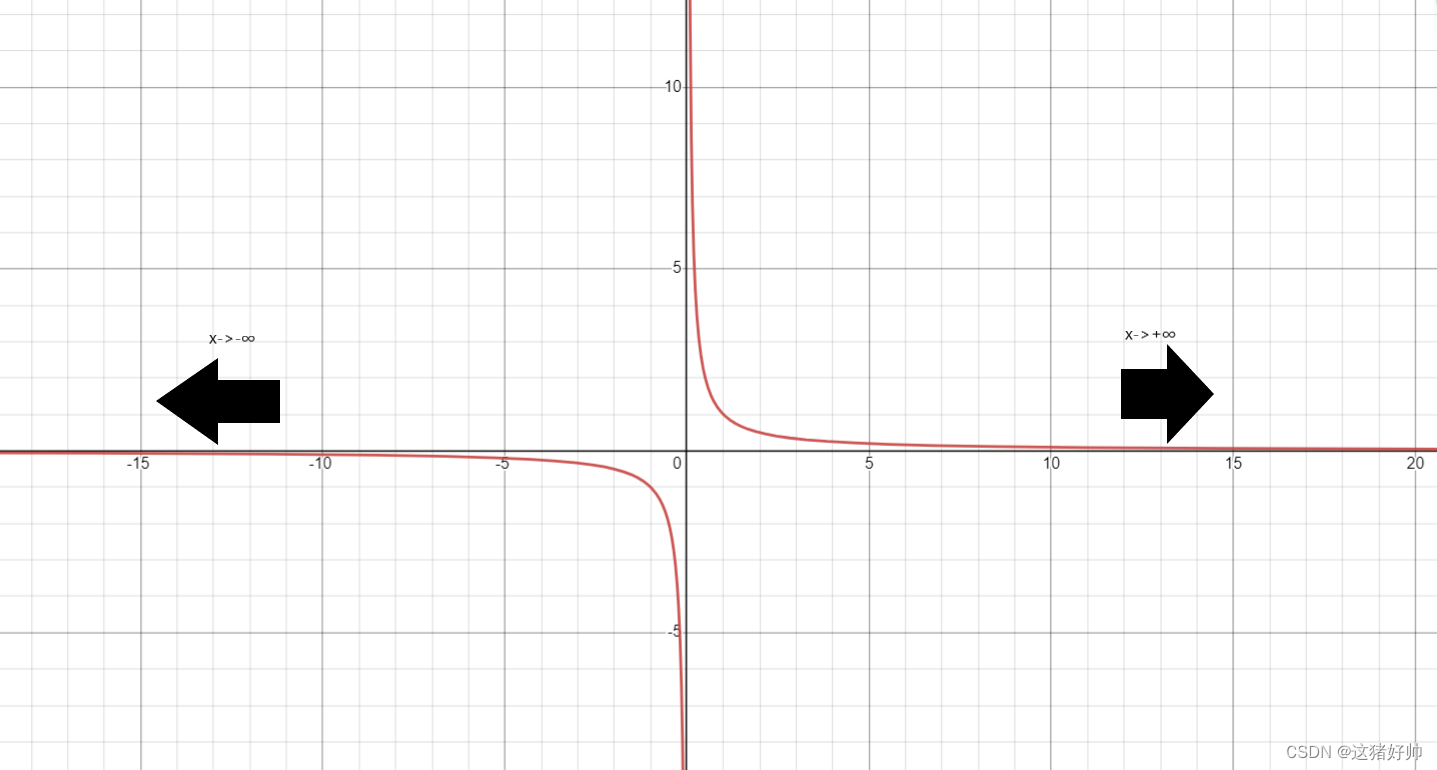
从图中我们可以得出以下结论:
若
lim
x
→
∞
f
(
x
)
=
a
,则
y
=
a
为
y
=
f
(
x
)
\lim_{x \to ∞}f(x)=a,则y=a为y=f(x)
limx→∞f(x)=a,则y=a为y=f(x)的水平渐近线
3.1.3、无穷小的比较
(1)、若
lim
α
(
x
)
β
(
x
)
=
0
\lim\frac{\alpha(x)}{\beta(x)}=0
limβ(x)α(x)=0,则称
α
(
x
)
\alpha(x)
α(x)是
β
(
x
)
\beta(x)
β(x)的高阶无穷小
记为
α
(
x
)
=
o
(
β
(
x
)
)
\alpha(x)=o(\beta(x))
α(x)=o(β(x))
(2)、若
lim
α
(
x
)
β
(
x
)
=
∞
\lim\frac{\alpha(x)}{\beta(x)}=∞
limβ(x)α(x)=∞,则称
α
(
x
)
\alpha(x)
α(x)是
β
(
x
)
\beta(x)
β(x)的低阶无穷小
(3)、若
lim
α
(
x
)
β
(
x
)
=
a
,
a
≠
0
\lim\frac{\alpha(x)}{\beta(x)}=a,a≠0
limβ(x)α(x)=a,a=0,则称
α
(
x
)
\alpha(x)
α(x)与
β
(
x
)
\beta(x)
β(x)是同阶无穷小
(4)、若
lim
α
(
x
)
β
(
x
)
=
1
\lim\frac{\alpha(x)}{\beta(x)}=1
limβ(x)α(x)=1,则称
α
(
x
)
\alpha(x)
α(x)与
β
(
x
)
\beta(x)
β(x)是等价无穷小
记为
α
(
x
)
\alpha(x)
α(x)~
β
(
x
)
\beta(x)
β(x)
(5)、若
lim
α
(
x
)
[
β
(
x
)
]
k
=
a
≠
0
,
k
>
0
\lim\frac{\alpha(x)}{[\beta(x)]^k}=a≠0,k>0
lim[β(x)]kα(x)=a=0,k>0,则称
α
(
x
)
\alpha(x)
α(x)是
β
(
x
)
\beta(x)
β(x)的k阶无穷小
当 x → 0 x \to 0 x→0时, n 1 + x − 1 ^n\sqrt{1+x}-1 n1+x−1~ 1 n x \frac{1}{n}x n1x
【证明】
即证:
lim
x
→
0
n
1
+
x
−
1
x
=
1
n
\lim_{x \to 0}\frac{^n\sqrt{1+x}-1}{x}=\frac{1}{n}
limx→0xn1+x−1=n1
令
n
1
+
x
−
1
=
t
,
x
=
(
1
+
t
)
n
−
1
^n\sqrt{1+x}-1=t,x=(1+t)^n-1
n1+x−1=t,x=(1+t)n−1
原式
=
lim
t
→
0
t
(
1
+
t
)
n
−
1
=\lim_{t \to 0}\frac{t}{(1+t)^n-1}
=limt→0(1+t)n−1t
二项式展开:
(
a
+
b
)
n
=
C
n
0
a
n
−
0
b
0
+
C
n
1
a
n
−
1
b
1
+
.
.
.
+
C
n
k
a
n
−
k
b
k
+
C
n
n
a
0
b
n
(a+b)^n=C_n^0a^{n-0}b^0+C_n^1a^{n-1}b^1+...+C_n^ka^{n-k}b^k+C_n^na^0b^n
(a+b)n=Cn0an−0b0+Cn1an−1b1+...+Cnkan−kbk+Cnna0bn
根据二项式展开原式
=
lim
t
→
0
t
n
t
+
n
(
n
−
1
)
2
t
2
+
.
.
.
=
1
n
=\lim_{t \to 0}\frac{t}{nt+\frac{n(n-1)}{2}t^2+...}=\frac{1}{n}
=limt→0nt+2n(n−1)t2+...t=n1
证毕
定理:
α
(
x
)
\alpha(x)
α(x)~
β
(
x
)
⇚
⇛
α
(
x
)
=
β
(
x
)
+
o
(
β
(
x
)
)
\beta(x)\Lleftarrow\Rrightarrow\alpha(x)=\beta(x)+o(\beta(x))
β(x)⇚⇛α(x)=β(x)+o(β(x))
【证明】
证明
α
(
x
)
−
β
(
x
)
⇛
α
(
x
)
=
β
(
x
)
+
o
(
β
(
x
)
)
\alpha(x)-\beta(x)\Rrightarrow\alpha(x)=\beta(x)+o(\beta(x))
α(x)−β(x)⇛α(x)=β(x)+o(β(x))
即证明:
α
(
x
)
−
β
(
x
)
β
(
x
)
=
0
\frac{\alpha(x)-\beta(x)}{\beta(x)}=0
β(x)α(x)−β(x)=0
α
(
x
)
−
β
(
x
)
β
(
x
)
=
α
(
x
)
β
(
x
)
−
1
=
0
\frac{\alpha(x)-\beta(x)}{\beta(x)}=\frac{\alpha(x)}{\beta(x)}-1=0
β(x)α(x)−β(x)=β(x)α(x)−1=0
证明
α
(
x
)
−
β
(
x
)
⇚
α
(
x
)
=
β
(
x
)
+
o
(
β
(
x
)
)
\alpha(x)-\beta(x)\Lleftarrow\alpha(x)=\beta(x)+o(\beta(x))
α(x)−β(x)⇚α(x)=β(x)+o(β(x))
两边同除
β
(
x
)
:
α
(
x
)
β
(
x
)
=
1
\beta(x):\frac{\alpha(x)}{\beta(x)}=1
β(x):β(x)α(x)=1
定理:设 α ( x ) ∼ α 1 ( x ) , β ( x ) ∼ β 1 ( x ) \alpha(x)\sim\alpha_1(x),\beta(x)\sim\beta_1(x) α(x)∼α1(x),β(x)∼β1(x),且 lim α 1 ( x ) β 1 ( x ) \lim\frac{\alpha_1(x)}{\beta_1(x)} limβ1(x)α1(x),则 lim α ( x ) β ( x ) = lim α 1 ( x ) β 1 ( x ) \lim\frac{\alpha(x)}{\beta(x)}=\lim\frac{\alpha_1(x)}{\beta_1(x)} limβ(x)α(x)=limβ1(x)α1(x)
【证明】
lim
α
(
x
)
β
(
x
)
=
lim
α
(
x
)
α
1
(
x
)
×
α
1
(
x
)
β
(
x
)
β
1
(
x
)
×
β
1
(
x
)
=
lim
α
1
(
x
)
β
1
(
x
)
\lim\frac{\alpha(x)}{\beta(x)}=\lim\frac{\frac{\alpha(x)}{\alpha_1(x)}\times\alpha_1(x)}{\frac{\beta(x)}{\beta_1(x)}\times\beta_1(x)}=\lim\frac{\alpha_1(x)}{\beta_1(x)}
limβ(x)α(x)=limβ1(x)β(x)×β1(x)α1(x)α(x)×α1(x)=limβ1(x)α1(x)
证毕
3.1.4、常用等价无穷小代换
当
x
∼
0
x\sim0
x∼0时
x
∼
sin
x
∼
tan
x
∼
arctan
x
∼
arcsin
x
∼
ln
(
1
+
x
)
∼
e
x
−
1
∼
ln
(
1
+
1
+
x
2
)
x\sim\sin x\sim\tan x\sim\arctan x\sim\arcsin x\sim\ln(1+x)\sim e^x-1\sim\ln(1+\sqrt{1+x^2})
x∼sinx∼tanx∼arctanx∼arcsinx∼ln(1+x)∼ex−1∼ln(1+1+x2)
log
a
(
1
+
x
)
∼
x
ln
a
\log_a(1+x)\sim\frac{x}{\ln a}
loga(1+x)∼lnax
1
2
x
2
∼
x
−
ln
(
1
+
x
)
∼
1
−
cos
x
\frac{1}{2}x^2\sim x-\ln(1+x)\sim1-\cos x
21x2∼x−ln(1+x)∼1−cosx
1
6
x
3
∼
x
−
sin
x
∼
arcsin
x
−
x
\frac{1}{6}x^3\sim x-\sin x\sim\arcsin x-x
61x3∼x−sinx∼arcsinx−x
1
3
x
3
∼
tan
x
−
x
∼
x
−
arctan
x
\frac{1}{3}x^3\sim \tan x-x\sim x-\arctan x
31x3∼tanx−x∼x−arctanx
1
2
x
3
∼
tan
x
−
sin
x
\frac{1}{2}x^3\sim \tan x-\sin x
21x3∼tanx−sinx
α
x
∼
(
1
+
x
)
α
−
1
\alpha x\sim(1+x)^\alpha-1
αx∼(1+x)α−1
3.2、无穷大
3.2.1、定义
定义:若
lim
x
→
x
0
f
(
x
)
=
∞
\lim_{x \to x_0}f(x) = ∞
limx→x0f(x)=∞,则称
f
(
x
)
f(x)
f(x)是
x
→
x
0
x \to x_0
x→x0时的无穷大量
即:若对任意给定的
M
>
0
M >0
M>0,总存在
δ
>
0
\delta>0
δ>0
当
0
<
∣
x
−
x
0
∣
<
δ
0 <|x-x_0|<\delta
0<∣x−x0∣<δ时,恒有
∣
f
(
x
)
∣
>
M
|f(x)|>M
∣f(x)∣>M
例:
lim
x
→
0
1
x
=
∞
\lim_{x \to 0}\frac{1}{x} = ∞
x→0limx1=∞
即:
1
x
\frac{1}{x}
x1是
x
→
0
x \to 0
x→0时的无穷大量
3.2.2、正无穷大与负无穷大
正无穷大:
lim
x
→
x
0
f
(
x
)
=
+
∞
\lim_{x \to x_0}f(x)=+∞
limx→x0f(x)=+∞
负无穷大:
lim
x
→
x
0
f
(
x
)
=
−
∞
\lim_{x \to x_0}f(x) =-∞
limx→x0f(x)=−∞
注意:正负无穷大量都是无穷大,无穷大包括了正负无穷大,而正负无穷大是无穷大的特殊情况
3.2.3、几何意义
我们以
lim
x
→
0
1
x
=
∞
\lim_{x \to 0}\frac{1}{x}=∞
limx→0x1=∞为例,如图为
f
(
x
)
=
1
x
f(x)=\frac{1}{x}
f(x)=x1
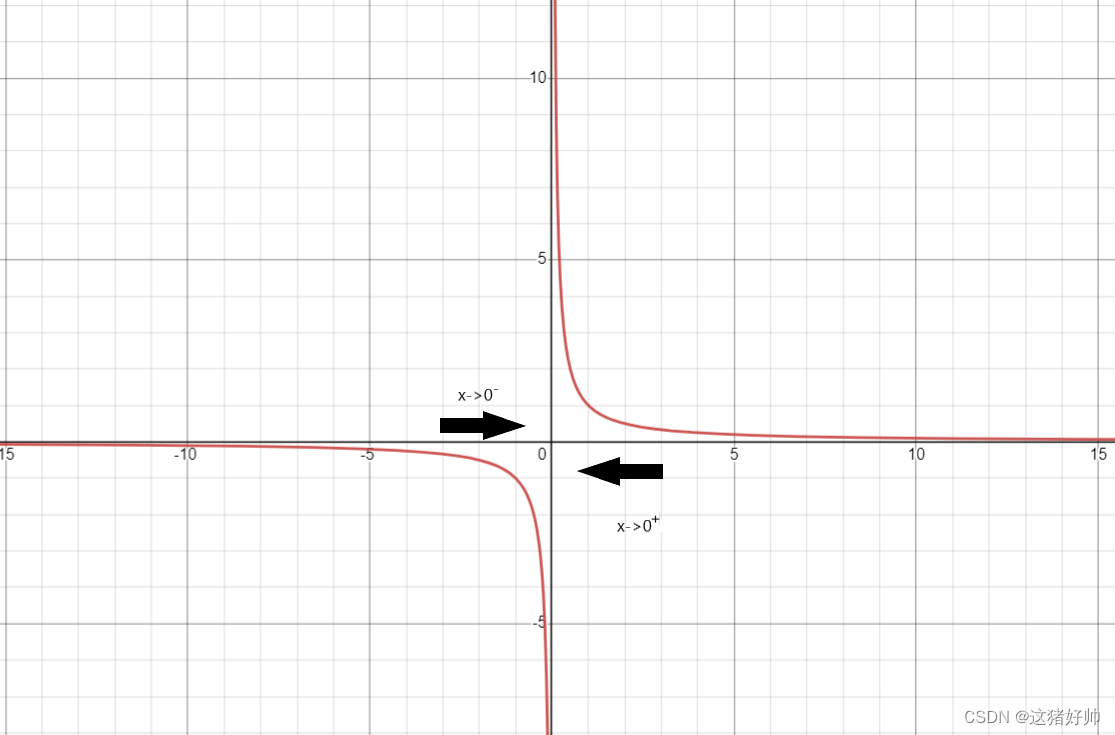
从图中我们可以得出以下结论:
1、若
lim
x
→
x
0
f
(
x
)
=
∞
则
x
=
x
0
为
y
=
f
(
x
)
\lim_{x \to x_0}f(x) =∞则x=x_0为y=f(x)
limx→x0f(x)=∞则x=x0为y=f(x)的垂直渐近线
3.3、无穷大与无穷小的关系
定理:在同一极限过程中,如果
f
(
x
)
f(x)
f(x)是无穷大,则
1
f
(
x
)
\frac{1}{f(x)}
f(x)1是无穷小
反之,如果
f
(
x
)
f(x)
f(x)是无穷小,且
f
(
x
)
≠
0
f(x)≠0
f(x)=0,则
1
f
(
x
)
\frac{1}{f(x)}
f(x)1是无穷大
注意:因为无穷小量也可能是0,所以这里必须要有 f ( x ) ≠ 0 f(x)≠0 f(x)=0
4、极限运算法则
4.1、基本定理
定理1:两个无穷小的和是无穷小
【证明】
令
lim
x
→
x
0
f
(
x
)
=
0
\lim_{x \to x_0}f(x)=0
limx→x0f(x)=0
lim
x
→
x
1
g
(
x
)
=
0
\lim_{x \to x_1}g(x)=0
limx→x1g(x)=0
∀
ϵ
>
0
,
∃
δ
1
,
当
0
<
∣
x
−
x
0
∣
<
δ
1
时
,
∣
f
(
x
)
∣
<
ϵ
\forall\epsilon>0,\exist\delta_1,当0<|x-x_0|<\delta_1时,|f(x)|<\epsilon
∀ϵ>0,∃δ1,当0<∣x−x0∣<δ1时,∣f(x)∣<ϵ
∀
ϵ
>
0
,
∃
δ
2
,
当
0
<
∣
x
−
x
0
∣
<
δ
2
时
,
∣
g
(
x
)
∣
<
ϵ
\forall\epsilon>0,\exist\delta_2,当0<|x-x_0|<\delta_2时,|g(x)|<\epsilon
∀ϵ>0,∃δ2,当0<∣x−x0∣<δ2时,∣g(x)∣<ϵ
令
δ
=
m
i
n
\delta=min
δ=min{
δ
1
,
δ
2
\delta_1,\delta_2
δ1,δ2},当
x
<
δ
x<\delta
x<δ时
$|f(x)|+|g(x)|<
2
ϵ
2\epsilon
2ϵ
证毕
推广:有限个无穷小的和为无穷小
注意:一定要是有限个无穷小
定理2:有界函数与无穷小的乘积是无穷小
【证明】
令有界函数
∣
g
(
x
)
∣
≤
M
,
x
∈
U
˚
(
x
,
δ
1
)
|g(x)|\leq M,x\in\mathring U(x,\delta_1)
∣g(x)∣≤M,x∈U˚(x,δ1)
令
lim
x
→
x
0
f
(
x
)
=
0
\lim_{x \to x_0}f(x)=0
limx→x0f(x)=0
即:
∀
ϵ
>
0
,
∃
δ
2
>
0
,
\forall\epsilon>0,\exist \delta_2>0,
∀ϵ>0,∃δ2>0,当
0
<
∣
x
<
x
0
∣
<
δ
2
0<|x<x_0|<\delta_2
0<∣x<x0∣<δ2时,
∣
f
(
x
)
∣
<
ϵ
|f(x)|<\epsilon
∣f(x)∣<ϵ
令
δ
=
m
i
n
\delta=min
δ=min{
δ
1
,
δ
2
\delta_1,\delta_2
δ1,δ2}
得:
∣
f
(
x
)
g
(
x
)
∣
≤
M
ϵ
|f(x)g(x)| \leq M\epsilon
∣f(x)g(x)∣≤Mϵ
由
ϵ
\epsilon
ϵ的任意性
证毕
推广1:常数与无穷小的乘积是无穷小
推广2:有限个无穷小的积仍是无穷小
推广2我们可以先看两个无穷小的乘积:
首先我们根据局部有界性可以得出无穷小其实在
x
∈
U
˚
(
x
0
,
δ
)
x\in\mathring U(x_0,\delta)
x∈U˚(x0,δ)是有界的
即转化为:有界乘无穷小=无穷小
既然两个无穷小的乘积是无穷小,即有限个无穷小的乘积也是无穷小
4.2、极限的四则运算
定理3:若
lim
f
(
x
)
=
A
,
lim
g
(
x
)
=
B
,
那么:
\lim f(x)=A,\lim g(x)=B,那么:
limf(x)=A,limg(x)=B,那么:
1、
lim
(
f
(
x
)
±
g
(
x
)
)
=
lim
f
(
x
)
±
lim
g
(
x
)
\lim(f(x)\pm g(x))=\lim f(x)\pm\lim g(x)
lim(f(x)±g(x))=limf(x)±limg(x)
2、
lim
(
f
(
x
)
×
g
(
x
)
)
=
lim
f
(
x
)
×
lim
g
(
x
)
\lim(f(x)\times g(x))=\lim f(x)\times\lim g(x)
lim(f(x)×g(x))=limf(x)×limg(x)
3、
lim
f
(
x
)
g
(
x
)
=
lim
f
(
x
)
lim
g
(
x
)
(
B
≠
0
)
\lim\frac{f(x)}{g(x)}=\frac{\lim f(x)}{\lim g(x)}(B≠0)
limg(x)f(x)=limg(x)limf(x)(B=0)
定理3的证明我们主要用到一个结论就是无穷小的定理:
一点处的极限就等于这一点的函数值
±
\pm
±无穷小
lim
x
→
x
0
f
(
x
)
=
A
⇚
⇛
f
(
x
)
=
A
+
α
(
x
)
\lim_{x \to x_0}f(x) =A\Lleftarrow\Rrightarrow f(x) =A+\alpha(x)
limx→x0f(x)=A⇚⇛f(x)=A+α(x)
【证】
1、证明:
lim
(
f
(
x
)
±
g
(
x
)
)
=
lim
f
(
x
)
±
lim
g
(
x
)
\lim(f(x)\pm g(x))=\lim f(x)\pm\lim g(x)
lim(f(x)±g(x))=limf(x)±limg(x)
f
(
x
)
=
A
+
α
(
x
)
,
g
(
x
)
=
B
+
β
(
x
)
f(x)=A+\alpha(x),g(x)=B+\beta(x)
f(x)=A+α(x),g(x)=B+β(x)
f
(
x
)
+
g
(
x
)
=
A
+
α
(
x
)
+
B
+
β
(
x
)
=
A
+
B
f(x)+g(x)=A+\alpha(x)+B+\beta(x)=A+B
f(x)+g(x)=A+α(x)+B+β(x)=A+B
证毕
2、证明:
lim
(
f
(
x
)
×
g
(
x
)
)
=
lim
f
(
x
)
×
lim
g
(
x
)
\lim(f(x)\times g(x))=\lim f(x)\times\lim g(x)
lim(f(x)×g(x))=limf(x)×limg(x)
f
(
x
)
=
A
+
α
(
x
)
,
g
(
x
)
=
B
+
β
(
x
)
f(x)=A+\alpha(x),g(x)=B+\beta(x)
f(x)=A+α(x),g(x)=B+β(x)
f
(
x
)
×
g
(
x
)
=
(
A
+
α
(
x
)
)
(
B
+
β
(
x
)
)
=
A
B
+
A
β
(
x
)
+
α
(
x
)
B
+
α
(
x
)
β
(
x
)
=
A
B
f(x)\times g(x)=(A+\alpha(x))(B+\beta(x))= AB+A\beta(x)+\alpha(x)B+\alpha(x)\beta(x)=AB
f(x)×g(x)=(A+α(x))(B+β(x))=AB+Aβ(x)+α(x)B+α(x)β(x)=AB
证毕
3、证明
lim
f
(
x
)
g
(
x
)
=
lim
f
(
x
)
lim
g
(
x
)
(
B
≠
0
)
\lim\frac{f(x)}{g(x)}=\frac{\lim f(x)}{\lim g(x)}(B≠0)
limg(x)f(x)=limg(x)limf(x)(B=0)
f
(
x
)
=
A
+
α
(
x
)
,
g
(
x
)
=
B
+
β
(
x
)
f(x)=A+\alpha(x),g(x)=B+\beta(x)
f(x)=A+α(x),g(x)=B+β(x)
f
(
x
)
g
(
x
)
=
A
+
α
(
x
)
B
+
β
(
x
)
=
A
B
\frac {f(x)}{g(x)}=\frac{A+\alpha(x)}{B+\beta(x)}=\frac {A}{B}
g(x)f(x)=B+β(x)A+α(x)=BA
证毕
注意:定理三得要求是两个函数极限都要存在,那么如果不存在得和差积商是什么呢?并且定理三可以推广到数列极限
1、存在
±
\pm
±不存在=不存在
我们可以假设如果存在+不存在=存在的话
即:不存在=存在+存在(而存在+存在一定存在)
此时就矛盾了
不存在
±
\pm
±不存在=不一定
例如:
lim
x
→
0
sin
1
x
+
s
i
n
1
x
\lim_{x \to 0}\sin\frac {1}{x}+sin\frac{1}{x}
limx→0sinx1+sinx1(不存在)
lim
x
→
0
sin
1
x
+
(
−
sin
1
x
)
=
0
\lim_{x \to 0}\sin\frac{1}{x}+(-\sin\frac{1}{x})=0
limx→0sinx1+(−sinx1)=0(存在)
存在
÷
/
×
÷/\times
÷/×不存在
=
=
=不一定
例如:
lim
x
→
0
x
sin
1
x
=
0
\lim_{x \to0}x\sin\frac{1}{x}=0
limx→0xsinx1=0(存在)
lim
x
→
0
1
×
sin
1
x
\lim_{x \to0}1\times\sin\frac{1}{x}
limx→01×sinx1(不存在)
不存在
÷
/
×
÷/\times
÷/×不存在=不一定
例如:
lim
x
→
0
1
x
×
1
x
\lim_{x \to 0}\frac{1}{x}\times\frac{1}{x}
limx→0x1×x1(不存在)
lim
n
→
∞
(
−
1
)
n
×
(
−
1
)
n
=
1
\lim_{n \to ∞}(-1)^n\times(-1)^n=1
limn→∞(−1)n×(−1)n=1(存在)
推论:如果
lim
f
(
x
)
\lim f(x)
limf(x)存在,而
c
c
c为常数,那么
lim
[
c
f
(
x
)
]
=
c
lim
f
(
x
)
\lim[cf(x)]=c\lim f(x)
lim[cf(x)]=climf(x)
推论:如果
lim
f
(
x
)
\lim f(x)
limf(x)存在,而
n
n
n为正整数,那么
lim
[
f
(
x
)
]
n
=
[
lim
f
(
x
)
]
n
\lim[f(x)]^n=[\lim f(x)]^n
lim[f(x)]n=[limf(x)]n
4.3、极限的比较大小
定理5:如果 φ ( x ) ≥ ψ ( x ) , 而 lim φ ( x ) = A , lim ψ ( x ) = B , φ(x)\geqψ(x),而\lim φ(x)=A,\lim \psi(x)=B, φ(x)≥ψ(x),而limφ(x)=A,limψ(x)=B,那么 A ≥ B A\geq B A≥B
【证明】证明
A
≥
B
A\geq B
A≥B
lim
(
φ
(
x
)
−
ψ
(
x
)
)
=
A
−
B
\lim (φ(x)-ψ(x))=A-B
lim(φ(x)−ψ(x))=A−B
∵
φ
(
x
)
−
ψ
(
x
)
≥
0
∵φ(x)−ψ(x)\geq0
∵φ(x)−ψ(x)≥0
∴
lim
(
φ
(
x
)
−
ψ
(
x
)
)
≥
0
,
即
A
−
B
≥
0
∴\lim (φ(x)-ψ(x))\geq0,即A-B\geq0
∴lim(φ(x)−ψ(x))≥0,即A−B≥0
证毕
4.4、复合函数的极限
定理6:设 y = f [ g ( x ) ] y=f[g(x)] y=f[g(x)]是由 y = f ( u ) , u = g ( x ) y=f(u),u=g(x) y=f(u),u=g(x)复合而成, lim x → x 0 g ( x ) = u 0 且 lim u → u 0 f ( u ) = a , 当 x ∈ U ˚ ( x 0 , δ 0 ) 时 \lim_{x \to x_0}g(x)=u_0且\lim_{u \to u_0}f(u)=a,当x \in\mathring U(x_0,\delta_0)时 limx→x0g(x)=u0且limu→u0f(u)=a,当x∈U˚(x0,δ0)时, g ( x ) ≠ u 0 g(x)≠u_0 g(x)=u0,则 lim x → x 0 f [ g ( x ) ] = a \lim_{x \to x_0}f[g(x)]=a limx→x0f[g(x)]=a
为什么需要
g
(
x
)
≠
u
0
g(x)≠u_0
g(x)=u0?我们先从定义角度来看,首先
lim
u
→
u
0
f
(
u
)
=
a
\lim_{u \to u_0} f(u)=a
limu→u0f(u)=a隐含得条件是:
u
→
u
0
,
但
u
≠
u
0
u \to u_0,但u≠u_0
u→u0,但u=u0,而此时
u
u
u被
g
(
x
)
g(x)
g(x)替换,那么
g
(
x
)
g(x)
g(x)也应该
g
(
x
)
→
u
0
,
但
g
(
x
)
≠
u
0
g(x) \to u_0,但g(x)≠u_0
g(x)→u0,但g(x)=u0,
g
(
x
)
g(x)
g(x)以
u
0
u_0
u0为极限则
g
(
x
)
g(x)
g(x)可以等于
u
0
u_0
u0,所以自然要加上
g
(
x
)
≠
u
0
g(x)≠u_0
g(x)=u0
反例:
f
(
u
)
=
x
2
−
1
x
−
1
f(u)=\frac{x^2-1}{x-1}
f(u)=x−1x2−1,
u
=
g
(
x
)
=
{
1
+
x
x
<
0
1
x
>
0
u=g(x)=\begin{cases} 1+x & x<0 \\ 1 & x>0 \\ \end{cases}
u=g(x)={1+x1x<0x>0,此时
f
[
g
(
x
)
]
=
{
(
1
+
x
)
2
−
1
x
x
<
0
无定义
x
>
0
f[g(x)]=\begin{cases} \frac{(1+x)^2-1}{x} & x< 0\\ 无定义 & x>0 \\ \end{cases}
f[g(x)]={x(1+x)2−1无定义x<0x>0
则此时
lim
x
→
x
0
f
[
g
(
x
)
]
=
不存在
\lim_{x \to x_0}f[g(x)]=不存在
limx→x0f[g(x)]=不存在
极限(下)超链接
【高等数学】极限(下)
![[Unity][VR]Passthrough2-创建一个基本的Passthrough应用](https://img-blog.csdnimg.cn/8a0746dde1e643edbd5de2fa3a7dfe5d.png)