python之计算市场技术指标

news2025/1/11 10:56:26

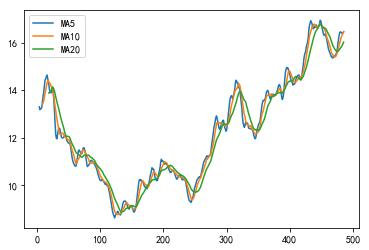
1、MA

MA指标是一种常用的技术指标，它是通过计算一定时间内的股价平均值来反映股价趋势的指标。通常，MA指标越平滑，就能更好地反映出股价的长期趋势。

MA指标的作用是帮助投资者识别股票价格的趋势。当股票价格的MA指标向上运动时，说明股票价格处于上升趋势中；当MA指标向下运动时，则说明股票价格处于下降趋势中；当MA指标水平移动时，则说明股票价格处于横盘震荡趋势中。

在使用MA指标时，通常会关注MA指标的交叉点。例如当短期移动平均线（快线）上穿长期移动平均线（慢线）时，被称为“金叉”，表明市场的短期趋势向上；反之，当短期移动平均线（快线）下穿长期移动平均线（慢线）时，被称为“死叉”，表明市场的短期趋势向下。此外，还可以观察MA指标与期货价格之间的相对位置，例如当期货价格在MA指标之上时，表明市场处于上升趋势，反之则为下降趋势。

MA指标是移动平均线的一种表现形式，被广泛应用于股票市场和期货市场的技术分析中。在使用MA指标时，需要根据具体的投资目标选择合适的计算期间，以便更准确地反映市场趋势和波动情况。

import talib
import pandas as pd
#import mpl_finance as mpf
import matplotlib.pyplot as plt
​
# 读取文件
df = pd.read_csv(r'F:\xxx')
# 计算MA指标
ma5_df = talib.MA(df['close'], timeperiod=5)
ma10_df = talib.MA(df['close'], timeperiod=10)
ma20_df = talib.MA(df['close'], timeperiod=20)
# 可视化
plt.rcParams['font.sans-serif'] = ['SimHei']
fig = plt.figure()
ax = fig.add_subplot(111)
# 绘制MA指标
ax.plot(ma5_df, label='MA5')
ax.plot(ma10_df, label='MA10')
ax.plot(ma20_df, label='MA20')
# 绘制K线图
#mpf.candlestick_ohlc(ax, df['open'], df['high'], df['low'], df['close'], width=0.6, colorup='red', colordown='green')
plt.legend(loc='best')
plt.show()
​

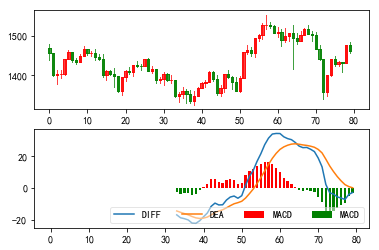
2、MACD指标

MACD称为异同移动平均线，是从双指数移动平均线发展而来的，由快的指数移动平均线（EMA12）减去慢的指数移动平均线（EMA26）得到快线DIF，再用2×（快线DIF-DIF的9日加权移动均线DEA）得到MACD柱。MACD的意义和双移动平均线基本相同，即由快、慢均线的离散、聚合表征当前的多空状态和股价可能的发展变化趋势，但阅读起来更方便。MACD的变化代表着市场趋势的变化，不同K线级别的MACD代表当前级别周期中的买卖趋势。

import numpy as np
import mpl_finance as mpf
import matplotlib.pyplot as plt
​
# 读取文件
df = pd.read_csv(r'xxx')
# 计算MACD指标
diff, dea, macd = talib.MACD(df['Close'], fastperiod=12, slowperiod=26, signalperiod=9)
# 可视化
plt.rcParams['axes.unicode_minus']=False
font1 = {'family': 'SimHei', 'weight': 'normal', 'size': 10}
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax2 = fig.add_subplot(212)
# 绘制K线图
mpf.candlestick2_ohlc(ax1, df['Open'], df['High'], df['Low'], df['Close'], width=0.6, colorup='red', colordown='green')
# 绘制DIFF和DEA曲线
ax2.plot(diff, label='DIFF')
ax2.plot(dea, label='DEA')
# 分别得到macd的bar是正值和负值的数据
macd_red = np.where(macd>0, macd, 0)
macd_green = np.where(macd<0, macd, 0)
# 绘制macd bar
ax2.bar(range(len(macd)), macd_red, width=0.6, facecolor='red', label='MACD')
ax2.bar(range(len(macd)), macd_green,width=0.6, facecolor='green', label='MACD')
# 显示图像
plt.legend(bbox_to_anchor=(1,0),loc=4,prop=font1,ncol=4,framealpha=0.5)
plt.show()
​

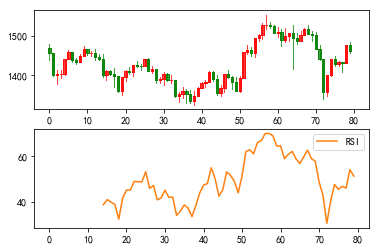
3、RSI指标

RSI指标，全称相对强弱指数（Relative Strength Index），最早被用于期货交易中，后来也被广泛应用于股票市场投资。该指标通过测量某一个期间内股价上涨总幅度占股价变化总幅度平均值的百分比，来评估多空力量的强弱程度，从而指导具体操作。

RSI指标的应用法则包括交叉、数值、形态和背离等多方面的判断原则。其特点是可以根据不同投资者的需求和偏好进行灵活调整，例如可以根据市场情况设置不同的期间参数，从而更好地适应市场的变化。

RSI指标的应用非常广泛，它可以帮助投资者把握市场趋势，寻找买卖时机，评估投资组合的风险等。然而，投资者也需要注意，该指标并不是万能的，它可能会出现虚假信号和误导情况，因此在具体操作中还需要结合其他指标和市场信息综合判断。

import numpy as np
import mpl_finance as mpf
import matplotlib.pyplot as plt
​
# 读取文件
df = pd.read_csv(r'xxx')
df=df[0:80]
# 计算RSI指标
rsi = talib.RSI(df['Close'], timeperiod = 14)
# 可视化
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax2 = fig.add_subplot(212)
# 绘制K线图
mpf.candlestick2_ohlc(ax1, df['Open'], df['High'], df['Low'], df['Close'], width=0.6, colorup='red', colordown='green')
# 绘制RSI曲线
ax2.plot(0, np.mean(rsi))  # 使上下坐标对应
ax2.plot(rsi, label='RSI')
# 显示图像
plt.legend()
plt.show()
​

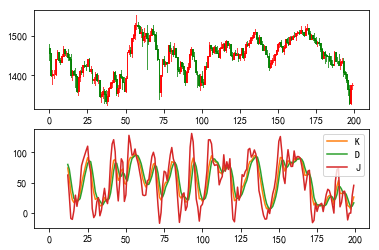
4、KDJ指标

KDJ指标是一种常用的技术分析指标，全称为随机指标（Stochastic Oscillator），最初用于期货市场的分析，后来也被广泛用于股市的中短期趋势分析。

KDJ指标是通过计算最后一个计算周期的未成熟随机值RSV，以及根据平滑移动平均线的方法来计算K值、D值与J值，并绘成曲线图来研判股票走势。它起先是在期货市场上被广泛运用，后来被引入到股票市场分析中，帮助投资者把握股票市场的趋势。

一般来说，KDJ指标的参考周期可以设定为9日、9周或90日等，也可以根据投资者自己的需要来设定。该指标的三条线，即K线、D线和J线，通常会随着股票市场的波动而上下波动。

当K线、D线和J线三线同时向上金叉的时候，说明股票市场处于强势阶段，可以适当持仓或加仓；当三线出现死叉的时候，说明市场可能将出现回调或反转，建议投资者可以考虑适当减仓或离场。此外，当K线和D线同时处于80以上的时候，说明市场处于超买阶段，可能会面临调整；反之，当K线和D线同时处于20以下的时候，说明市场处于超卖阶段，可能会面临反弹。

虽然KDJ指标在股票市场的分析中具有一定的参考价值，但投资者也需要注意其局限性。比如，该指标可能会出现“钝化”现象，即在高位或低位过于频繁地交叉，从而发出不准确的信号。此外，KDJ指标也并不能保证100%的正确率，投资者在使用该指标时还应当结合其他指标和市场信息进行综合判断。

import numpy as np
import mpl_finance as mpf
import matplotlib.pyplot as plt
​
# 读取文件
df = pd.read_csv(r'xxx')
df=df[0:200]
# 计算KDJ指标
K, D = talib.STOCH(df['High'], df['Low'], df['Close'], fastk_period=9, slowk_period=3, slowd_period=3)
J = 3*K - 2*D
# 可视化
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax2 = fig.add_subplot(212)
# 绘制K线图
mpf.candlestick2_ohlc(ax1, df['Open'], df['High'], df['Low'], df['Close'], width=0.6, colorup='red', colordown='green')
# 绘制KDJ曲线
ax2.plot(0, np.mean(K))    # 使上下坐标对应
ax2.plot(K, label='K')
ax2.plot(D, label='D')
ax2.plot(J, label='J')
# 显示图像
plt.legend()
plt.show()
​

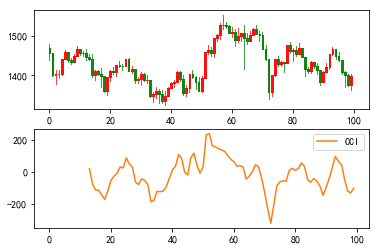
5、CCI指标

CCI指标是一种常用的技术分析指标，全称是顺势指标（Commodity Channel Index），由美国股市技术分析师唐纳德·蓝伯特（Donald Lambert）于20世纪80年代提出，专门用于测量股价、外汇或贵金属交易是否超出常态分布范围，属于超买超卖类指标中较特殊的一种。

CCI指标的理论基础是“能量是因，股价是果”。该指标通过统计学的原理，引入价格与固定期间的股价平均区间的偏离程度的概念，强调了股价平均绝对偏差在股市技术分析中的重要性。与其他超买超卖型指标类似，它的波动范围在正无穷大和负无穷大之间，但它并不以0为中轴线。

在具体使用上，CCI指标可以用于股票市场的研判，也可以用于期货市场的判断。与大多数利用股票的收盘价、开盘价、最高价或最低价而发明出的各种技术分析指标不同，CCI指标是根据价格与固定期间的股价平均区间的偏离程度的概念来做分析，能够更好地把握股价的趋势。

import numpy as np
import mpl_finance as mpf
import matplotlib.pyplot as plt
​
# 读取文件
df = pd.read_csv(r'xxx')
df=df[0:100]
# 计算CCI指标
CCI = talib.CCI(df['high'], df['low'], df['close'], timeperiod=14)
# 可视化
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax2 = fig.add_subplot(212)
# 绘制K线图
mpf.candlestick2_ohlc(ax1, df['open'], df['high'], df['low'], df['close'], width=0.6, colorup='red', colordown='green')
# 绘制CCI曲线
ax2.plot(0, np.mean(CCI))  # 使上下坐标对应
ax2.plot(CCI, label='CCI')
# 显示图像
plt.legend()
plt.show()
​

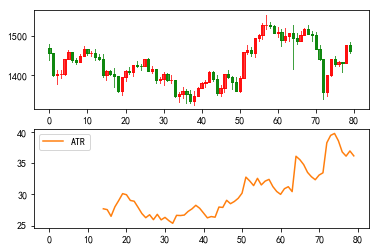
6、ATR指标

ATR指标，全称真实波幅（Average True Range），是一种用于衡量市场波动率的指标。该指标主要应用于了解股价的震荡幅度和节奏，在窄幅整理行情中用于寻找突破时机。

真实波幅（ATR）的计算公式为：TR=∣最高价-最低价∣和∣昨收-最高价∣的较大值和∣昨收-最低价∣的较大值；ATR=TR的N日简单移动平均。参数N通常设置为14日。

ATR指标的应用法则包括以下几点：

  • 常态时，波幅围绕均线上下波动。
  • 极端行情时，波幅上下幅度剧烈加大。
  • 当波幅TR过高，并且股价上涨过快时，应卖出。
  • 当波幅TR过低，并且真实波幅ATR连创新低时，表明股价已经进入窄幅整理行情中，随时将面临突破。
import numpy as np
import mpl_finance as mpf
import matplotlib.pyplot as plt
​
# 读取文件
df = pd.read_csv(r'xxx')
df=df[0:80]
# 计算ATR指标
ATR = talib.ATR(df['high'], df['low'], df['close'], timeperiod=14)
# 可视化
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax2 = fig.add_subplot(212)
# 绘制K线图
mpf.candlestick2_ohlc(ax1, df['open'], df['high'], df['low'], df['close'], width=0.6, colorup='red', colordown='green')
# 绘制ATR曲线
ax2.plot(0, np.mean(ATR))  # 使上下坐标对应
ax2.plot(ATR, label='ATR')
# 显示图像
plt.legend()
plt.show()
​

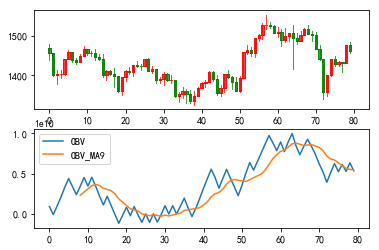
7、OBV指标

OBV指标是一种技术指标，全称是“On Balance Volume”，中文名为“能量潮”。它是由美国的约瑟夫·格兰维尔在1963年开发出来的。OBV通过计算成交量的变化来衡量股市的买入和卖出压力，是一种量价分析法。

OBV指标的研判通常与股票的价格趋势有关。该指标是通过统计成交量变动的趋势来推测股价趋势的一种方法。简单来说，当股票价格上升而OBV指标也相应上升时，这可能表明买入压力大，股价可能继续上涨。反之，当股票价格下跌而OBV指标也相应下降时，这可能表明卖出压力大，股价可能继续下跌。

import numpy as np
import mpl_finance as mpf
import matplotlib.pyplot as plt
​
# 读取文件
df = pd.read_csv(r'xxx')
df=df[0:80]
# 计算OBV指标
OBV = talib.OBV(df['close'], df['volume'])
# 计算OBV的9日均线
OBV_MA = talib.MA(OBV, timeperiod = 9)
# 可视化
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax2 = fig.add_subplot(212)
# 绘制K线图
mpf.candlestick2_ohlc(ax1, df['open'], df['high'], df['low'], df['close'], width=0.6, colorup='red', colordown='green')
# 绘制OBV曲线
ax2.plot(OBV, label='OBV')
ax2.plot(OBV_MA, label='OBV_MA9')
# 显示图像
plt.legend()
plt.show()
​
​

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1082445.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

分类网络的评价指标

分类网络的评价指标

之前一直是做目标检测的研究&#xff0c;在目标检测中主要有两个任务&#xff0c;一个是分类回归&#xff0c;一个是位置回归&#xff0c;所用的评价指标有&#xff1a;AP&#xff0c;mAP&#xff0c;Recall&#xff0c;Precision&#xff0c;F1值&#xff0c;前两个用的一般最…
阅读更多...
论文学习记录--零样本学习(zero-shot learning)

论文学习记录--零样本学习(zero-shot learning)

Socher R, Ganjoo M, Manning C D, et al. Zero-shot learning through cross-modal transfer[J]. Advances in neural information processing systems, 2013, 26. 注&#xff1a;中文为机翻 zero-shot learning&#xff1a;通过学习类别之间的关系和属性&#xff0c;使得模型…
阅读更多...
每日leetcode_LCP01猜数字

每日leetcode_LCP01猜数字

每日leetcode_LCP01猜数字 记录自己的成长&#xff0c;加油。 题目出处&#xff1a;LCP 01. 猜数字 - 力扣&#xff08;LeetCode&#xff09; 题目 解题 class Solution {public int game(int[] guess, int[] answer) {int count 0;for (int i 0 ; i< guess.length; i){…
阅读更多...
修正两个shapefile之间的数字化错误

修正两个shapefile之间的数字化错误

目录 一、数据输入 二、测量拓扑容差 三、启用编辑 四、使用拓扑编辑工具 五、建立图层拓扑关系 六、待修改的图层设置为唯一可选图层 七、编辑折点 八、拖动折点至land图层折点 一、数据输入 二、测量拓扑容差 拓扑容差约为4~5m 三、启用编辑 四、使用拓扑编辑工具 五…
阅读更多...
系统移植--前言

系统移植--前言

移植 不同架构的处理器指令集不兼容&#xff0c;即便是相同的处理器架构&#xff0c;板卡不同驱动代码也不兼容 Linux是一个通用的内核并不是为某一个特定的处理器架构或板卡设计的&#xff0c;所以从官方获取Linux源码后我们要先经过相应的配置使其与我们当前的硬件平台相匹配…
阅读更多...
Java数据结构第十七章、手撕位图

Java数据结构第十七章、手撕位图

给40亿个不重复的无符号整数&#xff0c;没排过序。给一个无符号整数&#xff0c;如何快速判断一个数是否在这40亿个数中。【腾讯】 1. 遍历&#xff0c;时间复杂度O(N) 2. 排序(O(NlogN))&#xff0c;利用二分查找: logN 3. 位图解决 数据是否在给定的整形数据中&#xff0c;结…
阅读更多...
重置Mac电脑的SMC怎么操作，重置SMC方法分享~

重置Mac电脑的SMC怎么操作，重置SMC方法分享~

SMC 负责管理 Mac 上的电源。重置 SMC 可以解决一些与电源或散热管理相关的不常见问题。今天重置SMC教程给大家分享一下&#xff0c;需要的小伙伴看过来&#xff01; 如何判断您是不是需要重置 SMC 若出现以下症状&#xff0c;则表明可能需要重置 SMC&#xff1a; 电池无法充电…
阅读更多...
Exim 中的漏洞！

Exim 中的漏洞！

我们将继续分享有关流行网络安全漏洞的最新信息。 Exim 中的 CVE-2023-42115漏洞&#xff01; CVE-2023-42115是开源 Exim 4 SMTP 邮件服务器项目中的一个远程代码执行漏洞。问题的严重性不容小觑。据我们的分析师称&#xff0c;目前网络中存在漏洞的 Exim 服务器超过 350 万台…
阅读更多...
18基于matlab的二阶动态系统的滑膜控制，程序已调通，可直接运行。标价为程序价格，不包含售后。程序保证可直接运行。

18基于matlab的二阶动态系统的滑膜控制，程序已调通，可直接运行。标价为程序价格，不包含售后。程序保证可直接运行。

基于matlab的二阶动态系统的滑膜控制&#xff0c;程序已调通&#xff0c;可直接运行。标价为程序价格&#xff0c;不包含售后。程序保证可直接运行。 18matlab滑膜控制 (xiaohongshu.com)
阅读更多...
【C++入门】命名空间详解(从零开始,冲击蓝桥杯)

【C++入门】命名空间详解(从零开始,冲击蓝桥杯)

C入门 命名空间 南喵小鸡汤程序员可以让步&#xff0c;却不可以退缩&#xff0c;可以羞涩&#xff0c;却不可以软弱&#xff0c;总之&#xff0c;程序员必须是勇敢的。一 . 命名空间的介绍二.命名空间的实际应用1.为什么要有命名空间我们在使用变量时,通常会为他定义一个名字,在…
阅读更多...
graphviz 绘制森林

graphviz 绘制森林

代码 digraph Forest {node [fontname"Arial", shapecircle, stylefilled, color"#ffffff", fillcolor"#0077be", fontsize12, width0.5, height0.5];edge [fontname"Arial", fontsize10, color"#333333", arrowsize0.5];/…
阅读更多...
Node基础概念，先了解一下

Node基础概念，先了解一下

Nodejs是基于Chrome V8引擎的服务器端JavaScript运行环境&#xff0c;也就是说可以在浏览器之外的主机上运行JavaScript。 NodeJS Nodejs有三部分组成&#xff1a;标准库、中间层和底层库。 标准库&#xff1a;是给开发人员直接调用的API&#xff0c;比如HTTP模块&#xff1b…
阅读更多...
Vulnhub Me-and-My-Girlfriend

Vulnhub Me-and-My-Girlfriend

一、信息收集 1.nmap 端口扫描 发现开发了22、80 2.访问ip&#xff0c;右击查看源代码 发现需要利用X-Forwarded-For 插件&#xff1a;X-Forwarded-For Header 挂上代理后&#xff1a; 出现以下页面&#xff1a; 先注册一个账户&#xff0c;然后再登录 发现有参数进行传…
阅读更多...
C语言系统化精讲（二）：C语言数组详解

C语言系统化精讲（二）：C语言数组详解

文章目录 一、数组的基本概念二、一维数组2.1 一维数组的定义2.2 一维数组初始化2.3 一维数组的引用 三、二维数组3.1 二维数组的定义3.2 二维数组初始化3.3 二维数组的引用 四、C语言数组是静态的&#xff0c;不能插入或删除元素五、C语言数组的越界和溢出5.1 数组越界5.2 数组…
阅读更多...
第一个2DGodot游戏-从零开始-逐步解析

第一个2DGodot游戏-从零开始-逐步解析

视频教程地址&#xff1a;https://www.bilibili.com/video/BV1Hw411v78Y/ 前言 大家好&#xff0c;这一集我将要带领大家完成官方文档里的第一个2DGodot游戏&#xff0c;从零开始&#xff0c;逐步解析&#xff0c;演示游戏的制作全过程&#xff0c;尽量让&#xff0c;就算是新…
阅读更多...
C++ - 包装器 - bind（）函数

C++ - 包装器 - bind（）函数

包装器 在 C 当中可能会有各种各样的可调用类型&#xff0c;比如 函数指针&#xff0c;仿函数&#xff0c;lambda 等等&#xff0c;那么这么多的可调用类型&#xff0c;我们在使用的时候就会犯迷糊&#xff0c;那可不可以统一控制一下呢&#xff1f; function包装器&#xff…
阅读更多...
关于SSA算法中矩阵的3种运算：转置、求逆、相乘

关于SSA算法中矩阵的3种运算：转置、求逆、相乘

1、矩阵转置 // 矩阵转置(二维矩阵)public static double[][] transposeTwo(double[][] matrix) {int rows matrix.length;int cols matrix[0].length;double[][] transposedMatrix new double[cols][rows];for (int i 0; i < rows; i) {for (int j 0; j < cols; j)…
阅读更多...
一篇博客带你学会关于Vuex使用

一篇博客带你学会关于Vuex使用

前言&#xff1a; 在我们之前我们的学习vue知识中&#xff0c;我们组件传递方式有父传子&#xff0c;子传父&#xff0c;这两种方法传递参数复杂&#xff0c;所以我们今天来学习Vuex&#xff0c;就可以解决这个传递的问题&#xff01;&#xff01;&#xff01; 一&#xff0c;V…
阅读更多...
【算法思考】端到端实例分割模型 SOLO

【算法思考】端到端实例分割模型 SOLO

目录 背景工作总结 背景 不同于语义分割&#xff0c;实例分割不仅需要输出图像的语义蒙版&#xff0c;还要对图像中不同的实例作区分。如下图所示&#xff0c;实例分割任务需要多不同的羊做区分&#xff0c;输出不同的实例蒙版。 由于图片中实例个数的不确定性&#xff0c;实例…
阅读更多...
第二章 C++的输出

第二章 C++的输出

系列文章目录 第一章 C的输入 文章目录 系列文章目录前言一、个人名片二、cout三、printf总结 前言 今天来学C的输出吧&#xff01; 一、个人名片 二、cout cout 三、printf printf 总结 最近懒得写博客怎么办&#xff1f;
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023