提示：努力生活，开心、快乐的一天

---

198. 打家劫舍

题目链接：198. 打家劫舍

💡解题思路

1. 当前房屋偷与不偷取决于 前一个房屋和前两个房屋是否被偷了
   当前状态和前面状态会有一种依赖关系，那么这种依赖关系都是动规的递推公式。
2. 动规五部曲：

• 确定dp数组以及下标的含义：dp[i]：考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]。
• 确定递推公式：决定dp[i]的因素就是第i房间偷还是不偷
  如果偷第i房间，那么dp[i] = dp[i - 2] + nums[i] ，即：第i-1房一定是不考虑的，找出 下标i-2（包括i-2）以内的房屋，最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。
  如果不偷第i房间，那么dp[i] = dp[i - 1]，即考 虑i-1房，（注意这里是考虑，并不是一定要偷i-1房，这是很多同学容易混淆的点）
  dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
• dp数组如何初始化：dp[0] = nums[0]；dp[1] = max(nums[0], nums[1])
• 确定遍历顺序：dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的，那么一定是从前到后遍历
• 举例推导dp数组：按照递推公式推导一下做推导，如果发现结果不对，就把dp数组打印出来

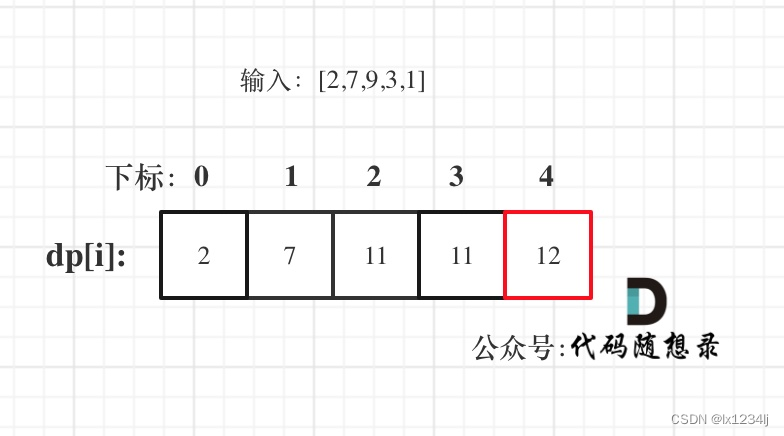
🤔遇到的问题

1. 不需要像之前的背包问题一样，初始化dp数组
2. 遍历从下标2开始遍历

💻代码实现

动态规划

var rob = function(nums) {
    let len = nums.length
    let dp = [nums[0], Math.max(nums[0], nums[1])]
    for (let i = 2; i < len; i++){
        dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i])
    }
    return dp[len-1]
};

🎯题目总结

当前房屋偷与不偷取决于 前一个房屋和前两个房屋是否被偷了，是非常经典的DP题目

---

213. 打家劫舍 II

题目链接：213. 打家劫舍 II

💡解题思路

1. 这道题目和198.打家劫舍 (opens new window)是差不多的，唯一区别就是成环了
   对于一个数组，成环的话主要有如下三种情况：

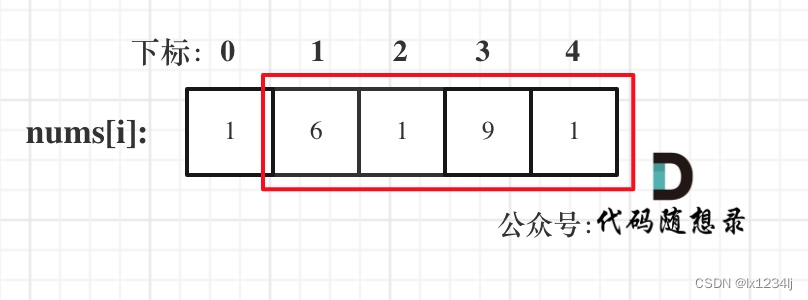
• 情况一：考虑不包含首尾元素
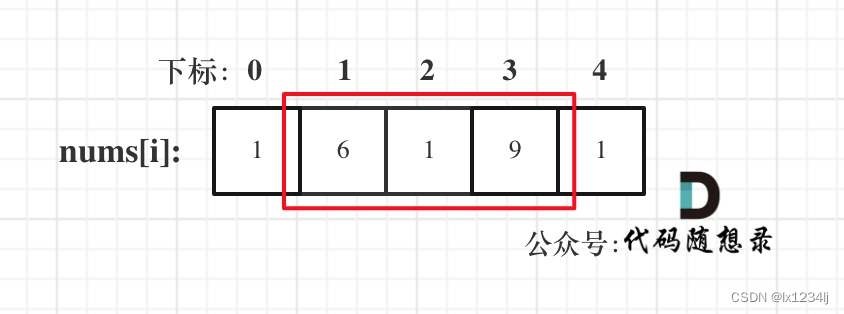
• 情况二：考虑包含首元素，不包含尾元素
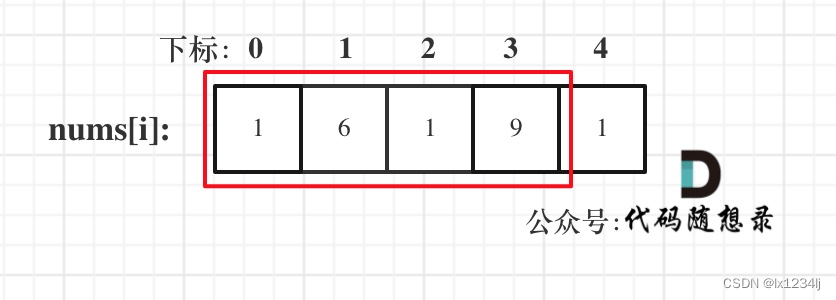
• 情况三：考虑包含尾元素，不包含首元素
  里用的是"考虑"，例如情况三，虽然是考虑包含尾元素，但不一定要选尾部元素！ 对于情况三，取nums[1] 和 nums[3]就是最大的。
  而情况二 和 情况三 都包含了情况一了，所以只考虑情况二和情况三就可以了

🤔遇到的问题

1. 调用原来的打家劫舍的代码，需要进行参数的修改

💻代码实现

动态规划

var rob = function (nums) {
    let len = nums.length
    if (len === 0) return 0
    if (len === 1) return nums[0]
    //不要尾 情况二
    let result2 = robRange(nums, 0, len - 2)
    //不要头 情况三
    let result1 = robRange(nums, 1, len - 1)
    return Math.max(result1, result2)

};
//与之前的没有环形的数组一样
const robRange = (nums, start, end) => {
    if (end === start) return nums[start]
    let len = nums.length
    let dp = new Array(len).fill(0)
    dp[start] = nums[start]
    dp[start+1] = Math.max(nums[start],nums[start+1])
    for (let i = start+2; i <= end; i++) {
        dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i])
    }
    return dp[end]
};

🎯题目总结

三种情况，情况一包含在情况二和情况三中。另外调用原来的方法需要进行改动，有数组的起始和结束为止的标识

---

337. 打家劫舍 III

题目链接：337. 打家劫舍 III

💡解题思路

1. 首先就要想到遍历方式，前中后序（深度优先搜索）还是层序遍历（广度优先搜索）。
   本题一定是要后序遍历，因为通过递归函数的返回值来做下一步计算。
   如果抢了当前节点，两个孩子就不能动，如果没抢当前节点，就可以考虑抢左右孩子（注意这里说的是“考虑”）
2. 动态规划其实就是使用状态转移容器来记录状态的变化，这里可以使用一个长度为2的数组，记录当前节点偷与不偷所得到的的最大金钱。
3. 以递归三部曲为框架，其中融合动规五部曲的内容：

• 确定递归函数的参数和返回值：这里我们要求一个节点 偷与不偷的两个状态所得到的金钱，那么返回值就是一个长度为2的数组，本题dp数组就是一个长度为2的数组！
• 确定终止条件：在遍历的过程中，如果遇到空节点的话，很明显，无论偷还是不偷都是0
• 确定遍历顺序：首先明确的是使用后序遍历。 因为要通过递归函数的返回值来做下一步计算。通过递归左节点，得到左节点偷与不偷的金钱。通过递归右节点，得到右节点偷与不偷的金钱。
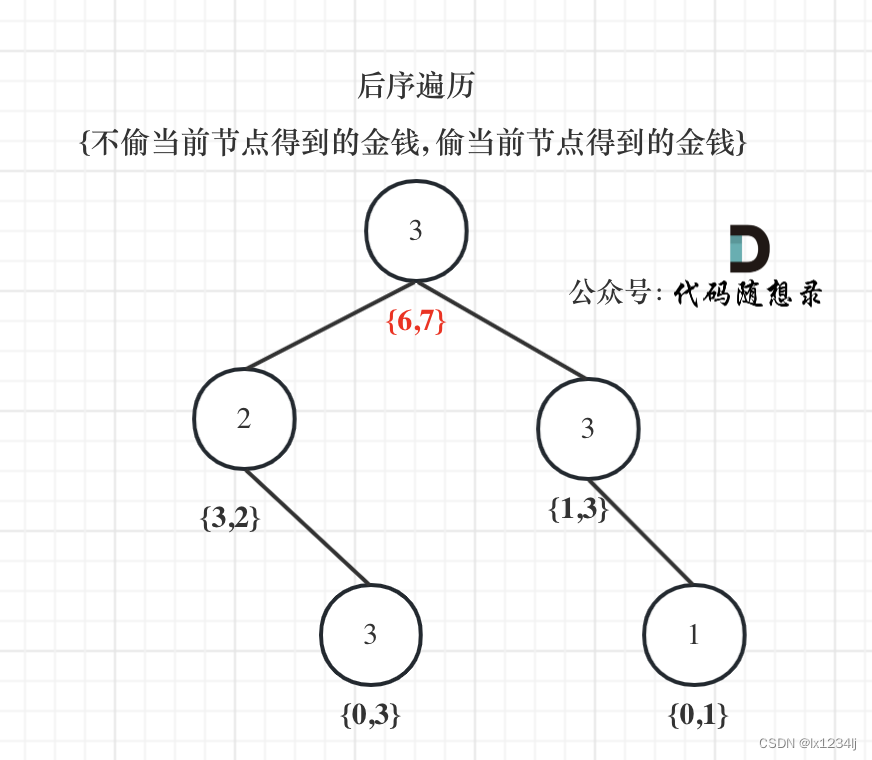
• 确定单层递归的逻辑：如果是偷当前节点，那么左右孩子就不能偷，val1 = cur->val + left[0] + right[0]; （如果对下标含义不理解就再回顾一下dp数组的含义）；如果不偷当前节点，那么左右孩子就可以偷，至于到底偷不偷一定是选一个最大的，所以：val2 = max(left[0], left[1]) + max(right[0], right[1]);最后当前节点的状态就是{val2, val1}; 即：{不偷当前节点得到的最大金钱，偷当前节点得到的最大金钱}
• 举例推导dp数组：以示例1为例，dp数组状态如下：（注意用后序遍历的方式推导）

🤔遇到的问题

1. 思路很难想到，基本是看着写出来的代码

💻代码实现

动态规划

const rob = root => {
    // 后序遍历函数
    const postOrder = node => {
        // 递归出口
        if (!node) return [0, 0];
        // 遍历左子树
        const left = postOrder(node.left);
        // 遍历右子树
        const right = postOrder(node.right);
        // 不偷当前节点，左右子节点都可以偷或不偷，取最大值
        const DoNot = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
        // 偷当前节点，左右子节点只能不偷
        const Do = node.val + left[0] + right[0];
        // [不偷，偷]
        return [DoNot, Do];
    };
    const res = postOrder(root);
    // 返回最大值
    return Math.max(...res);
};

🎯题目总结

只不过平时我们习惯了在一维数组或者二维数组上推导公式，一下子换成了树，就需要对树的遍历方式足够了解！

🎈今日心得

打家劫舍还不错，思路捋清楚以后，可以举一反三啦，打家劫舍III是真的难啊