gpu cuda矩阵转置

news2024/11/21 0:18:58

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

问题描述

给定1个二数组，利用gpu转置并返回结果。

cpu 算法


void cpu_matrix_trnspose(int in[N][M], int out[M][N]) {
	for (int y = 0; y < N; ++y) {
		for (int x = 0; x < M; ++x) {
			cpu_result[x][y] = matrix[y][x];
		}
	}
}

cpu耗时

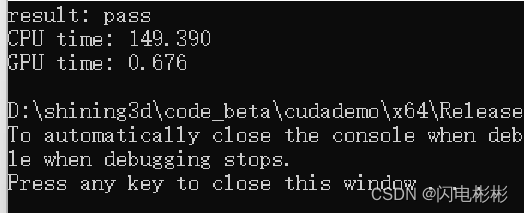
在这里插入图片描述

耗时149毫秒

gpu 算法-直接法

代码

__global__ void gpu_matrix_transpose(int in[N][M], int out[M][N]) {
	int x = threadIdx.x + blockDim.x*blockIdx.x;
	int y = threadIdx.y + blockDim.y*blockIdx.y;

	if (x < M && y < N) {
		out[x][y] = in[y][x];
	}
}

耗时分析

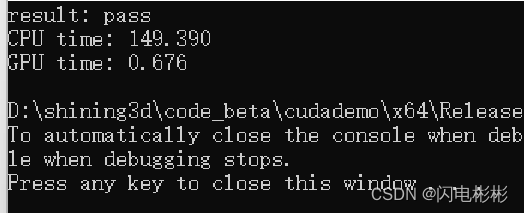
在这里插入图片描述

耗时0.676毫秒，提升了100多倍。

算法缺点

在gpu中数组是放在全局内存里，全局内存访问比较慢（相较于共享内存）。如果是连续访问则可以进行合并访存，效率上可以作一些弥补，如果一直随机访问效率会打折扣。

分析上述代码。

二维数组可以按行展开成一维数组。

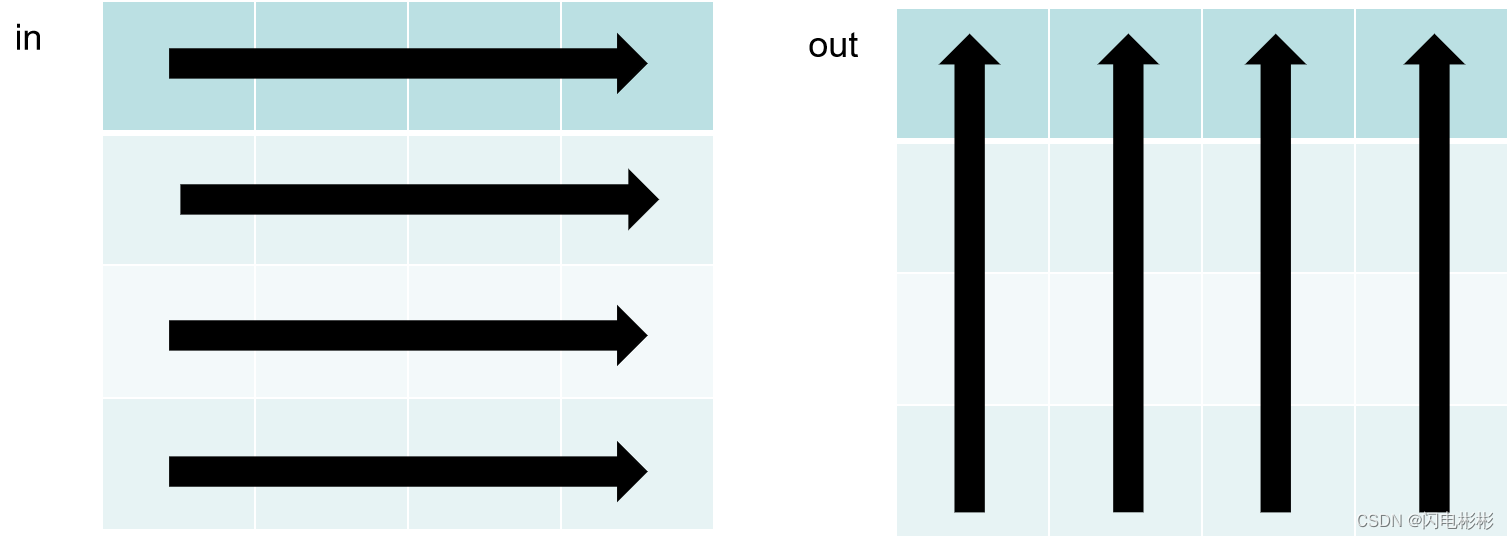
在这里插入图片描述

in[y][x]可以认为是按行访问（顺序访问）
out[x][y]则是按列访问，对于内存来说不是顺序访问，会降低效率。

gpu 算法分块法（块内顺序访问）

算法思路

共享内存访问效率比全局内存快速1个数量级。

但是共享内存大小有限制。

gpu中1个block内存所有线程可以共同访问一块共享内存。

block最多有1024个线程。

我们可以把矩阵分成多个（n*m）块，每个块32*32大小。

每个block可以对一个块进行转置。

转置1个块具体过程如下：

步骤1：把in第(1,2)块按行访问存入到共享内存
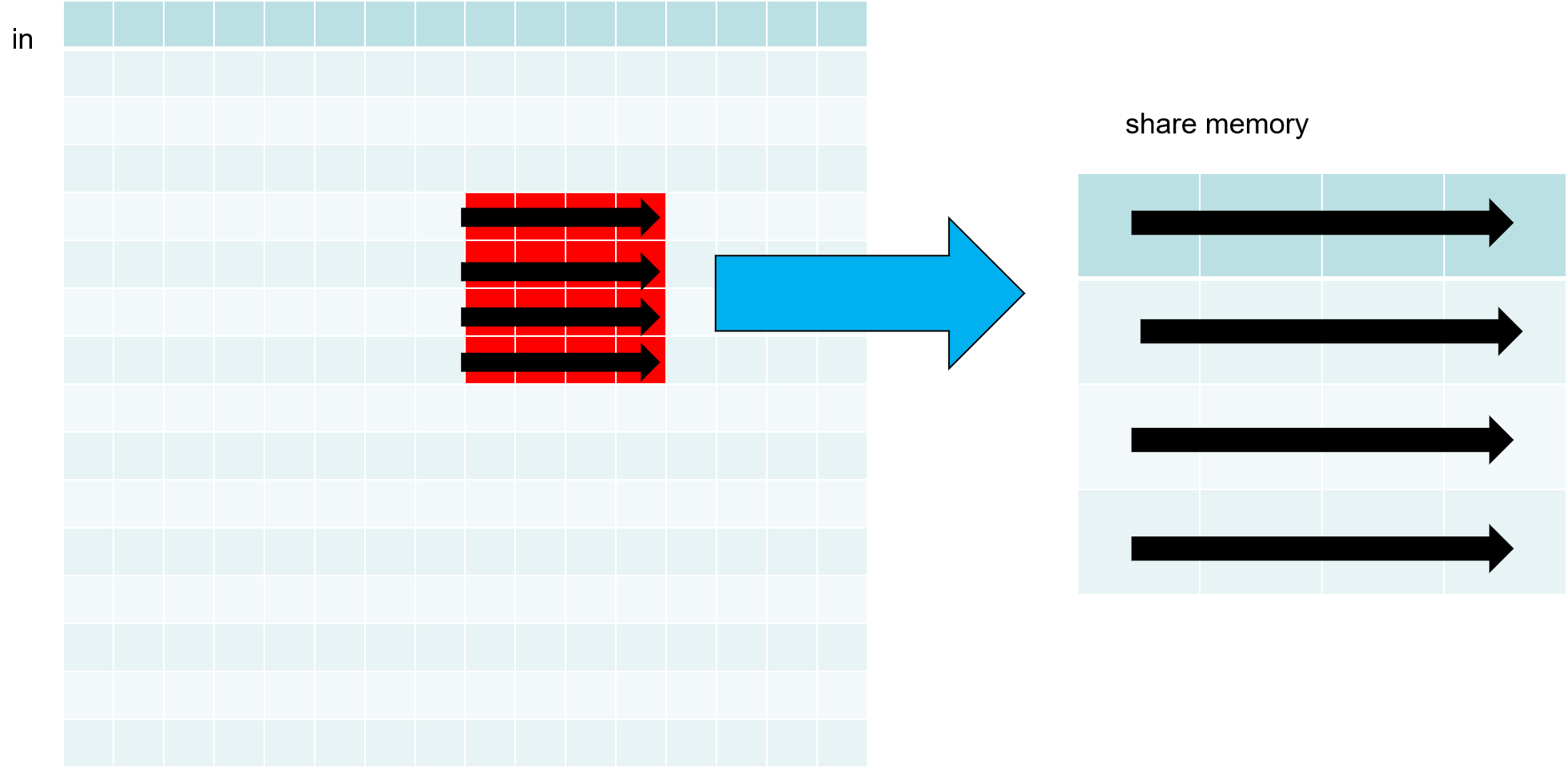
在这里插入图片描述
步骤2：把share memory按列访问共享内存按行存入到out第(2,1)块

在这里插入图片描述

这样在访问in, out时都做到了按行访问和写入。对于share memory 访问都很快，无关访问顺序。

代码


#include "cuda_runtime.h"
#include <math.h>
#include<vector>
#include "device_launch_parameters.h"

#include <stdio.h>

using namespace std;
typedef long long lld;

#define BLOCK_SIZE 32
#define M 3000
#define N 1000

__managed__ int matrix[N][M];
__managed__ int gpu_result[M][N];
__managed__ int cpu_result[M][N];

__global__ void gpu_matrix_transpose(int in[N][M], int out[M][N]) {
	int x = threadIdx.x + blockDim.x*blockIdx.x;
	int y = threadIdx.y + blockDim.y*blockIdx.y;

	if (x < M && y < N) {
		out[x][y] = in[y][x];
	}
}

__global__ void gpu_shared_matrix_transpose(int in[N][M], int out[M][N]) {
	int x = threadIdx.x + blockDim.x*blockIdx.x;
	int y = threadIdx.y + blockDim.y*blockIdx.y;

	__shared__ int ken[BLOCK_SIZE+1][BLOCK_SIZE+1];

	if (x < M && y < N) {
		ken[threadIdx.y][threadIdx.x] = in[y][x];
	}
	__syncthreads();

	int x1 = threadIdx.x + blockDim.y*blockIdx.y;
	int y1 = threadIdx.y + blockDim.x*blockIdx.x;
	if (x1 < N && y1 < M) {
		out[y1][x1] = ken[threadIdx.x][threadIdx.y];
	}
}

void cpu_matrix_trnspose(int in[N][M], int out[M][N]) {
	for (int y = 0; y < N; ++y) {
		for (int x = 0; x < M; ++x) {
			cpu_result[x][y] = matrix[y][x];
		}
	}
}


int main()
{
	for (int y = 0; y < N; ++y) {
		for (int x = 0; x < M; ++x) {
			matrix[y][x] = x + y * M;
		}
	}

	cudaEvent_t start, stop_gpu, stop_cpu;
	cudaEventCreate(&start);
	cudaEventCreate(&stop_gpu);
	cudaEventCreate(&stop_cpu);

	cudaEventRecord(start);
	cudaEventSynchronize(start);

	dim3 dimGrid((M+BLOCK_SIZE-1)/BLOCK_SIZE,(N+BLOCK_SIZE-1)/BLOCK_SIZE);
	dim3 dimBlock(BLOCK_SIZE, BLOCK_SIZE);

	for (int i = 0; i < 20; ++i) {
		gpu_shared_matrix_transpose <<<dimGrid,dimBlock>>>(matrix, gpu_result);
		cudaDeviceSynchronize();
	}
	cudaEventRecord(stop_gpu);
	cudaEventSynchronize(stop_gpu);

	cpu_matrix_trnspose(matrix, cpu_result);
	cudaEventRecord(stop_cpu);
	cudaEventSynchronize(stop_cpu);

	float time_cpu, time_gpu;
	cudaEventElapsedTime(&time_gpu, start, stop_gpu);
	cudaEventElapsedTime(&time_cpu, stop_gpu, stop_cpu);

	bool errors = false;
	for (int y = 0; y < N; ++y) {
		for (int x = 0; x < M; ++x) {
			if (cpu_result[y][x] != gpu_result[y][x]) errors = true;
		}
	}

	printf("result: %s\n", errors? "fault":"pass");
	printf("CPU time: %.3f\nGPU time: %.3f\n", time_cpu, time_gpu/20);

	cudaEventDestroy(start);
	cudaEventDestroy(stop_gpu);
	cudaEventDestroy(stop_cpu);

    return 0;
}