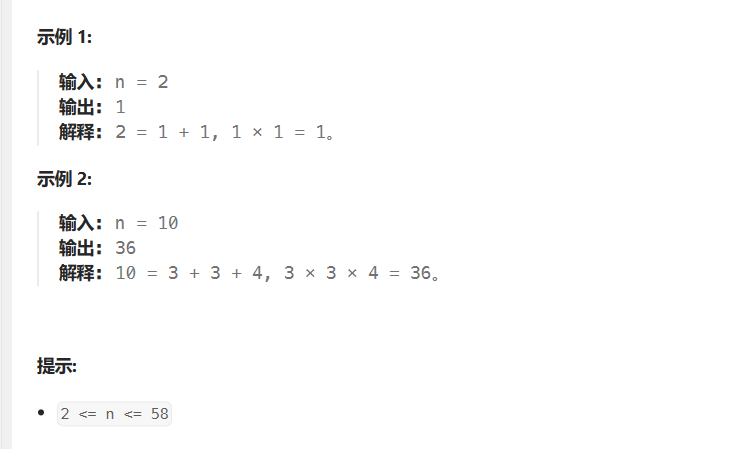狄拉克函数及其性质

news2024/11/13 8:50:23
  • 狄拉克函数及其性质

狄拉克函数

\delta(x)=\left\{\begin{matrix} \infty & x=0\\ 0&x\neq0 \end{matrix}\right.

\int_{-\epsilon}^{+\epsilon}\delta(x)dx=\int_{-\infty}^{+\infty}\delta(x)dx=1

近似处理

逼近近似

\lim_{\sigma\rightarrow0}\frac{1}{\sqrt{\pi}\sigma}e^{-x^2/\sigma^2}=\delta(x)

\lim_{\alpha\rightarrow\infty}\sqrt{\frac{\alpha}{\pi}}e^{i\pi/4}e^{-i\alpha x^2}=\delta(x)

\lim_{\alpha\rightarrow\infty}\frac{sin(\alpha x)}{\pi x}=\delta(x)

\lim_{\alpha\rightarrow\infty}\frac{sin^2\alpha x}{\pi\alpha x^2}=\delta(x)

\lim_{\epsilon\rightarrow0}\frac{e^{-|x|/\epsilon}}{2\epsilon}=\delta(x)

\lim_{\epsilon\rightarrow0}\frac{\epsilon}{x^2+\epsilon^2}=\pi\delta(x)

积分近似

\int_{-\infty}^{+\infty}e^{ikx}dk=2\pi\delta(x)

狄拉克函数的性质

\delta(ax)=\frac{1}{|a|}\delta(x)

\delta(-x)=\delta(x)

\int_{-\infty}^{+\infty}f(x)\delta(x-a)dx=f(a)

\int_{-\infty}^{+\infty}\delta(x-a)\delta(x-b)dx=\delta(a-b)

x\delta(x)=0

狄拉克函数的Hermite展开

2\delta(1-cos\theta)=\sum_{l=0}^\infty (2l+1)P_l(cos\theta)

\delta(x-x')=\sum_{n=0}^\infty \frac{e^{-\frac{1}{2}(x^2+x'^2)}}{\sqrt{\pi}2^n\cdot n!}H_n(x')H_n(x)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1080947.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【C++】【自用】STL六大组件：算法

【C++】【自用】STL六大组件：算法

文章目录 🔺sortstable_sort🔺reverse🔺swap🔺find🔺max/min🔺next_permutation/prev_permutation 全排列binary_searchlower_bound/upper_bound 求下界和上界set_union/set_intersection/set_difference 求…
阅读更多...
结构体课程自我理解

结构体课程自我理解

目录 1. 结构体类型的声明 1.2特殊的声明方法 1.3结构体的自引用 1.4 typedef 对结构体命名 2. 结构体变量的创建和初始化 3. 结构成员访问操作符 4. 结构体内存对⻬ 4.1下面给大伙4个练习题，有自我解析 4.2为什么存在内存对齐 4.3修改默认对齐数 5. …
阅读更多...
Centos中利用自带的定时器Crontab_实现mysql数据库自动备份_linux中mysql自动备份脚本---Linux运维工作笔记056

Centos中利用自带的定时器Crontab_实现mysql数据库自动备份_linux中mysql自动备份脚本---Linux运维工作笔记056

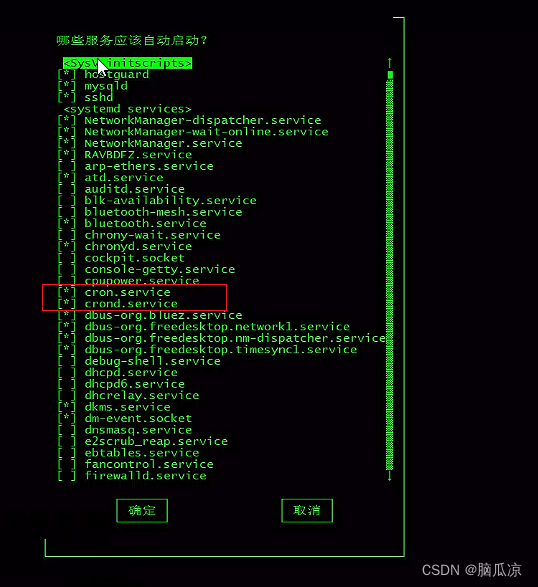
这个经常需要,怕出问题因而需要经常备份数据库,可以利用centos自带的定时器,配合脚本实现自动备份. 1.首先查看一下,这个crontab服务有没有打开: 执行:ntsysv 可以看到已经开机自启动了. 注意这个操作界面,用鼠标不行,需要用,tab按键,直接tab到确定,或取消,然后按回车回到命…
阅读更多...
如何下不可选中的文章

如何下不可选中的文章

背景： 看到了一篇比较有用的微信公众号文章（这个文章应该是跳转到了公众号外的网站的 url 了），想留档，但是手机选中不了。但是这个事情作为程序员，怎么能束手呢。 操作： 1、将微信公众号链接在…
阅读更多...
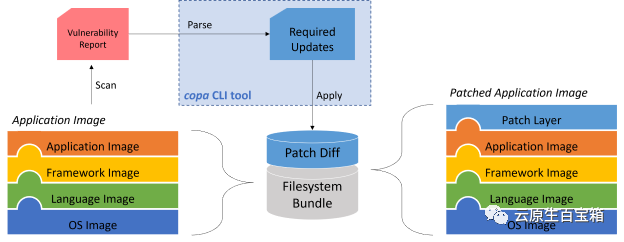
Copa：无需重建镜像，直接修补容器漏洞

Copa：无需重建镜像，直接修补容器漏洞

关注【云原生百宝箱】公众号，与你一起探讨应用迁移，GitOps，二次开发，解决方案，CNCF生态。 copa 是一个使用 Go 编写的 CLI 工具，基于 buildkit，可以根据像 Trivy 这样的流行工具的漏洞扫描结果直…
阅读更多...
LeetCode-343-整数拆分

LeetCode-343-整数拆分

题目描述： 给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k > 2 ），并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 题目链接： LeetCode-343-整数拆分 解题思路： 还是根据动规五…
阅读更多...
Centos (含Rocky-Linux) VSFTPD 简单设置

Centos (含Rocky-Linux) VSFTPD 简单设置

本文并非深入讨论vsftp配置的文章，仅以能连通为目的，适合那些临时需要上传点东西到服务器的场景。 一、安装 dnf -y updatednf -y install vsftpdsystemctl start vsftpdsystemctl enable vsftpd二、防火墙 开放21端口： firewall-cmd --zo…
阅读更多...
利用正则表达式进行数据采集和处理

利用正则表达式进行数据采集和处理

目录 一、正则表达式的概述 二、正则表达式在数据采集中的运用 1、匹配和提取数据 2、数据清洗 3、数据验证 三、Python中的re模块介绍 1、re.match()方法 2、re.search()方法 总结 正则表达式是一种强大的文本处理工具，它可以用于模式匹配、提取、替换等操…
阅读更多...
Android 自定义横向时间轴

Android 自定义横向时间轴

示例&#xff1a; 一、添加依赖 dependencies {******//添加RecyclerView的依赖包implementation androidx.recyclerview:recyclerview:1.2.1 } 二、页面代码 activity_main.xml: <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmln…
阅读更多...
大语言模型迎来重大突破！找到解释神经网络行为方法

大语言模型迎来重大突破！找到解释神经网络行为方法

前不久&#xff0c;获得亚马逊40亿美元投资的ChatGPT主要竞争对手Anthropic在官网公布了一篇名为《朝向单义性&#xff1a;通过词典学习分解语言模型》的论文&#xff0c;公布了解释经网络行为的方法。 由于神经网络是基于海量数据训练而成&#xff0c;其开发的AI模型可以生成…
阅读更多...
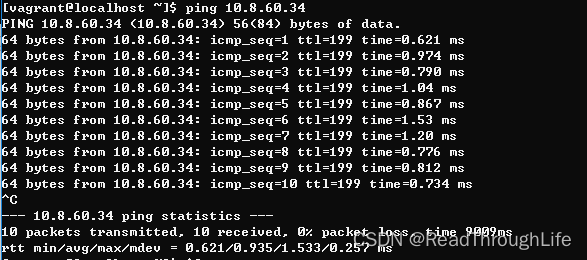
Virtual Box + Vagrant 快速搭建 Linux 虚拟开发环境

Virtual Box + Vagrant 快速搭建 Linux 虚拟开发环境

Virtual Box Vagrant 快速搭建 Linux 虚拟开发环境 1、根据自己所使用的操作系统平台&#xff0c;选择下载对应的虚拟机客户端软件 Virtual Box 并进行安装&#xff0c;这里选择的是 Virtual Box 7.0.10 Windows hosts 平台安装包。 选择安装目录为其他盘&#xff0c;避免默认…
阅读更多...
【C++】STL总结：理解六大核心组件、各个组件主要功能

【C++】STL总结：理解六大核心组件、各个组件主要功能

文章目录 六大核心组件的关联性1.容器2.迭代器3.算法4. 仿函数 / 函数对象5. 适配器 / 包装器6. 空间配置器 六大核心组件的关联性 1.容器 &#x1f517;&#x1f449;点击跳转 2.迭代器 &#x1f517;&#x1f449;点击跳转 3.算法 &#x1f517;&#x1f449;点击跳转 …
阅读更多...
安科瑞消防设备电源监控系统在城市建筑中的应用

安科瑞消防设备电源监控系统在城市建筑中的应用

安科瑞 崔丽洁 摘要&#xff1a;2021年十四五规划里&#xff0c;也都有写到关于绿色循环经济的议题。在这样一个背景下&#xff0c;建筑行业也需要为实现“双碳”目标作出改变&#xff0c;建筑行业飞速发展&#xff0c;大量高层建筑拔地而起&#xff0c;在为了响应国家对于建筑…
阅读更多...
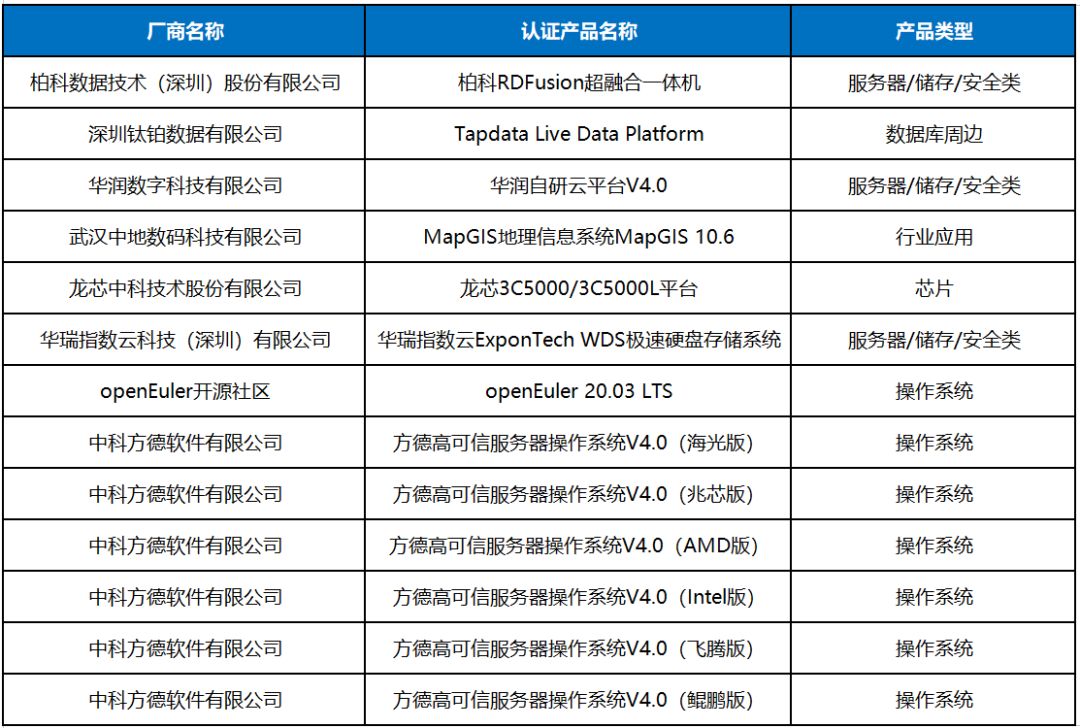
生态共建 | 7-9月，YashanDB与13款产品完成兼容互认证

生态共建 | 7-9月，YashanDB与13款产品完成兼容互认证

7-9月&#xff0c;深圳计算科学研究院崖山数据库系统YashanDB与柏科数据技术&#xff08;深圳&#xff09;股份有限公司、深圳钛铂数据有限公司、华润数字科技有限公司、武汉中地数码科技有限公司、龙芯中科技术股份有限公司、华瑞指数云科技&#xff08;深圳&#xff09;有限公…
阅读更多...
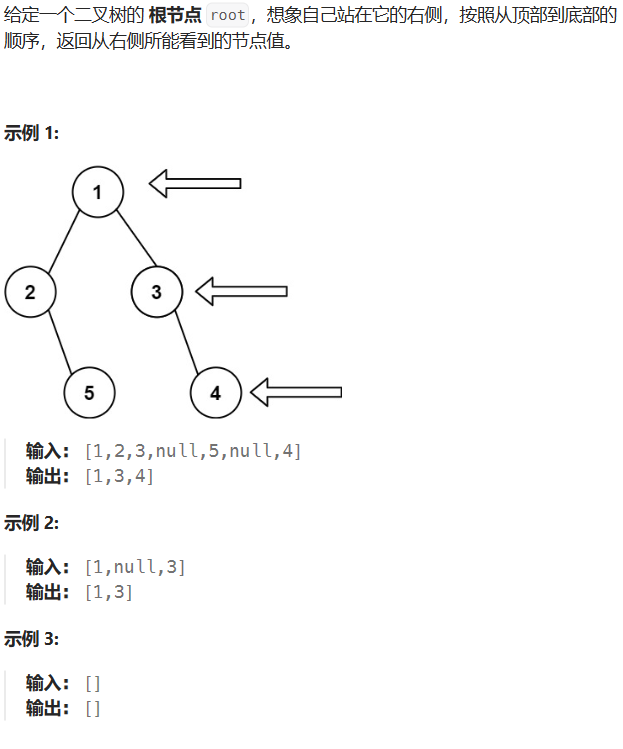
LeetCode-199-二叉树的右视图

LeetCode-199-二叉树的右视图

题目描述&#xff1a; 题目链接&#xff1a;LeetCode-199-二叉树的右视图 解题思路&#xff1a; 在 102 的基础之上进行改进&#xff0c;一维数组每次只保存 size1 时候的值 代码实现&#xff1a; class Solution {public List<Integer> rightSideView(TreeNode root) {i…
阅读更多...
【算法-动态规划】斐波那契第 n 项

【算法-动态规划】斐波那契第 n 项

&#x1f49d;&#x1f49d;&#x1f49d;欢迎来到我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里可以感受到一份轻松愉快的氛围&#xff0c;不仅可以获得有趣的内容和知识&#xff0c;也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学…
阅读更多...
网络初识（JAVA EE）

网络初识（JAVA EE）

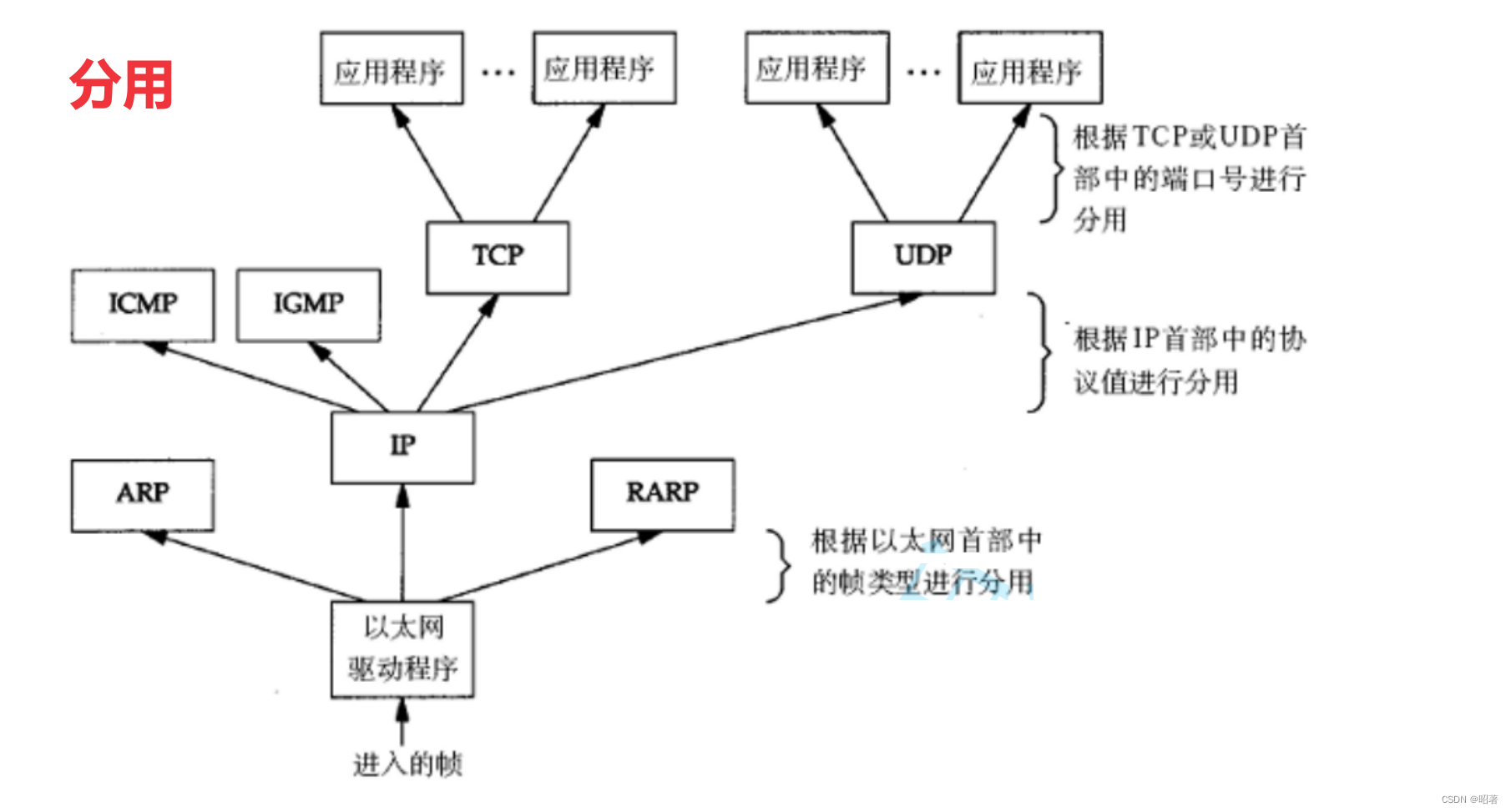
文章目录 一、网络发展史二、网络通信基础三、协议分层四、封装和分用 一、网络发展史 独立模式&#xff1a;计算机之间相互独立&#xff0c;每个终端都各自持有客户数据&#xff0c;且当处理一个业务时&#xff0c;按照业务流程进行 网络互连&#xff1a;将多台计算机连接在一…
阅读更多...
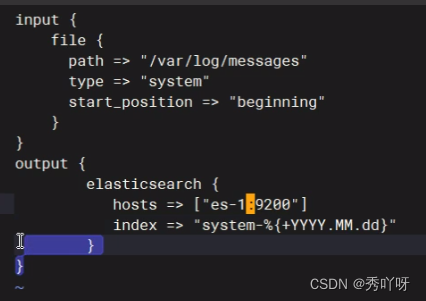
ELK集群 日志中心集群、kafka、logstash

ELK集群 日志中心集群、kafka、logstash

ES&#xff1a;用来日志存储 Logstash:用来日志的搜集&#xff0c;进行日志格式转换并且传送给别人&#xff08;转发&#xff09; Kibana:主要用于日志的展示和分析 kafka Filebeat:搜集文件数据 es-1 本地解析 vi /etc/hosts scp /etc/hosts es-2:/etc/hosts scp /etc…
阅读更多...
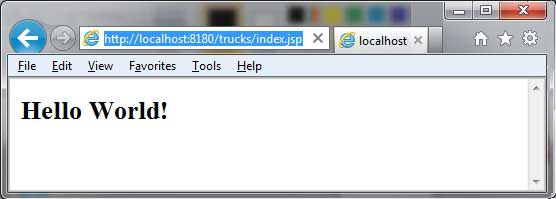
Maven Web应用

Maven Web应用

目录 创建 Web 应用 构建 Web 应用 部署 Web 应用 测试 Web 应用 本章节我们将学习如何使用版本控制系统 Maven 来管理一个基于 web 的项目&#xff0c;如何创建、构建、部署以及运行一个 web 应用。 创建 Web 应用 我们可以使用 maven-archetype-webapp 插件来创建一个简…
阅读更多...
景区经营系统如何落地运营？景区系统重点功能推荐

景区经营系统如何落地运营？景区系统重点功能推荐

在数字经济的引领下&#xff0c;文旅行业也迎来数字化转型的浪潮&#xff0c;需要借助数字化工具完成一整套景区经营管理落地方案。如蚓链数字化文旅系统拥有多端开发能力&#xff0c;可实现PC端、移动端、小程序等多端开发&#xff0c;让游客可随时随地畅游景区&#xff0c;提…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023