这里非常抱歉 没有做好动图 等我做好了动态单独做一期博客到时候大家结合动图将本篇博客联系起来看 更容易理解一些喔
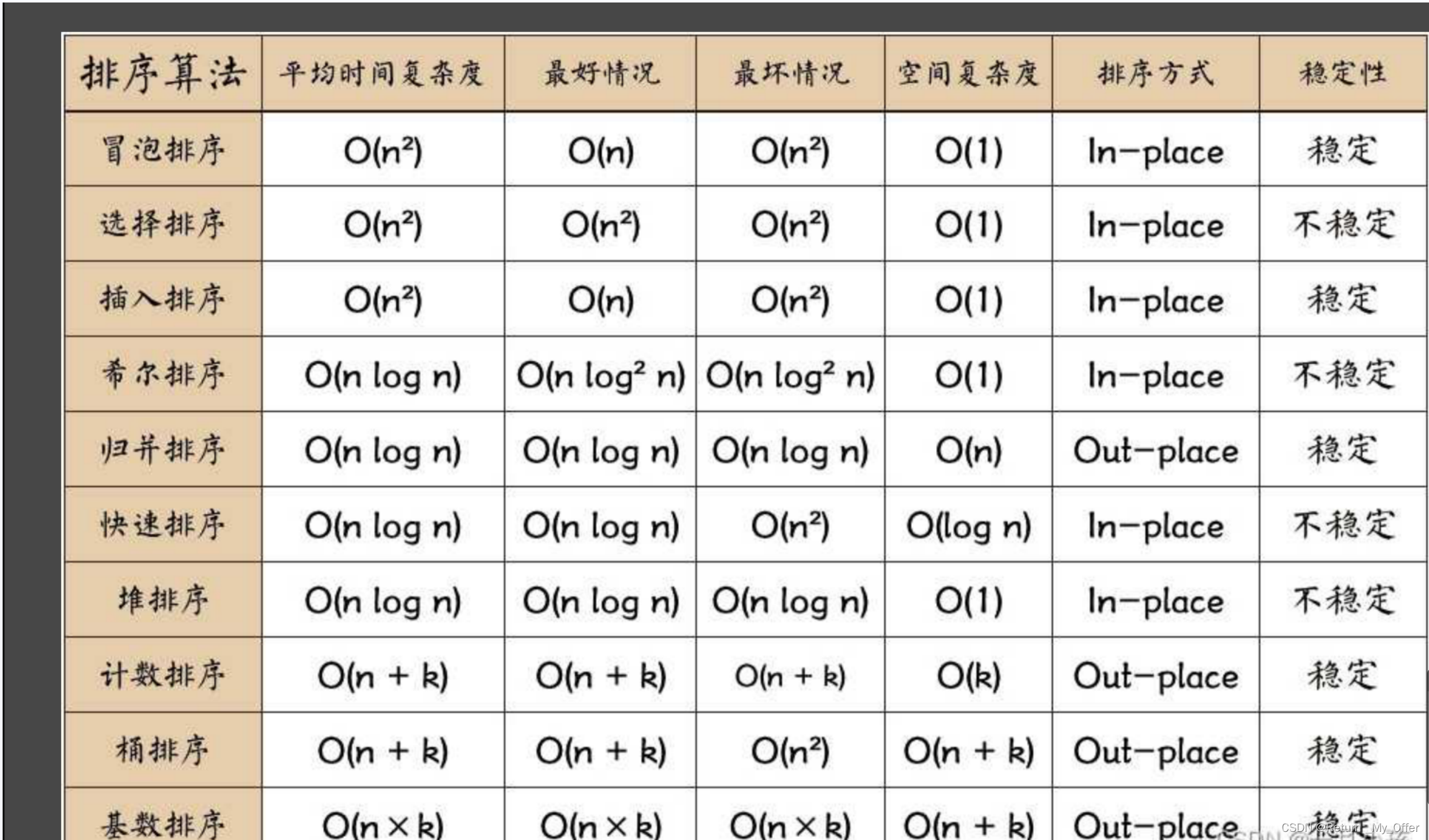
常见的数据结构中的排序算法有冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序、堆排序等。

冒泡排序：比较相邻的元素，如果前一个比后一个大，就交换它们的位置，一轮下来可以将最大的元素放到最后面。时间复杂度为O(n^2)。

1冒泡排序

void bubble_sort(int arr[], int len) {
    int i, j, temp;
    for (i = 0; i < len - 1; i++) {
        for (j = 0; j < len - 1 - i; j++) {
            if (arr[j] > arr[j + 1]) {
                temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

2选择排序

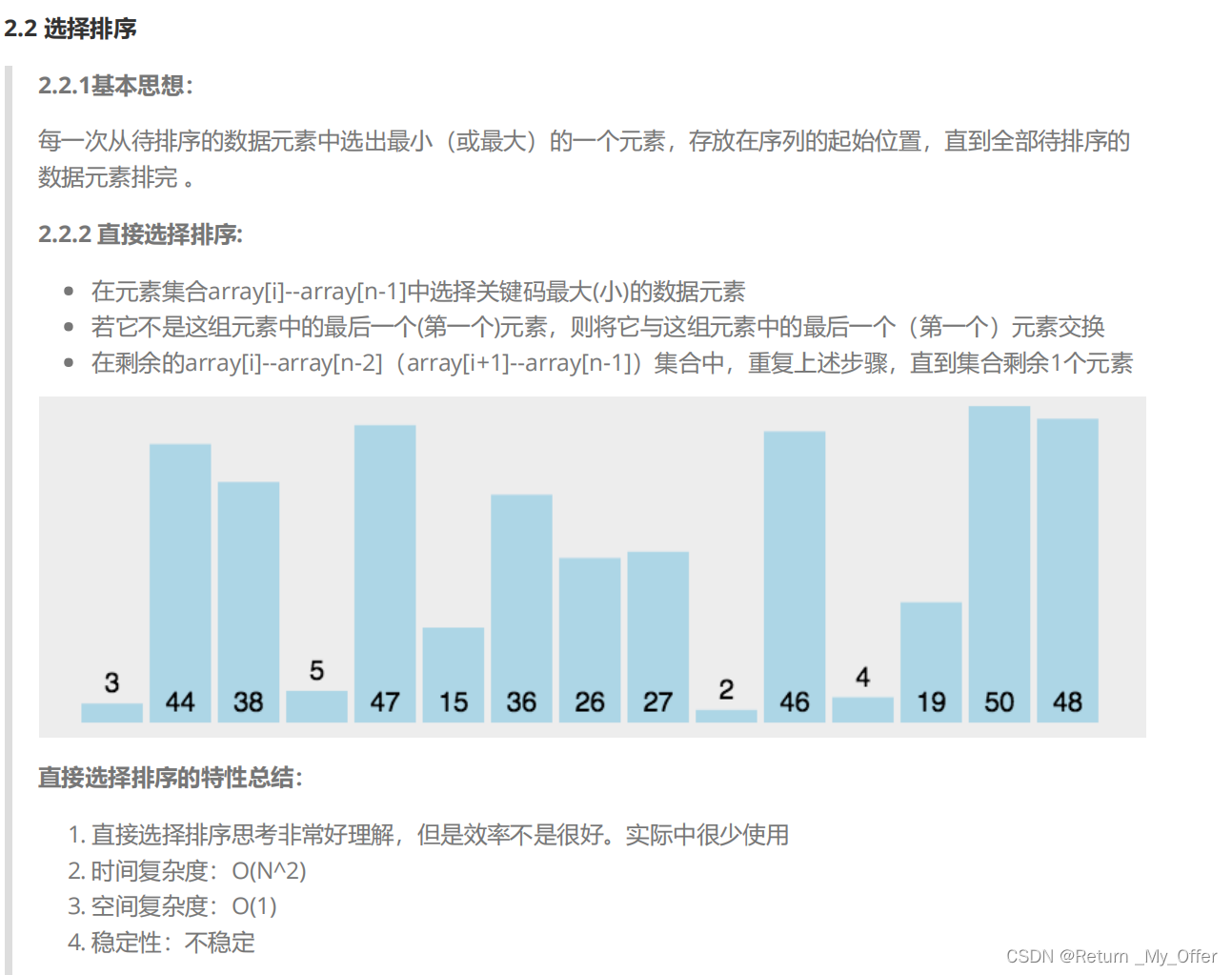
选择排序：每次从未排序的元素中选择最小的元素，放到已排序的末尾。时间复杂度为O(n^2)

void selection_sort(int arr[], int len) {
    int i, j, min_index, temp;
    for (i = 0; i < len - 1; i++) {
        min_index = i;
        for (j = i + 1; j < len; j++) {
            if (arr[j] < arr[min_index]) {
                min_index = j;
            }
        }
        if (min_index != i) {
            temp = arr[i];
            arr[i] = arr[min_index];
            arr[min_index] = temp;
        }
    }
}

3插入排序

void insertion_sort(int arr[], int len) {
    int i, j, temp;
    for (i = 1; i < len; i++) {
        temp = arr[i];
        for (j = i - 1; j >= 0 && arr[j] > temp; j--) {
            arr[j + 1] = arr[j];
        }
        arr[j + 1] = temp;
    }
}

4快速排序

//三数取中
int GetMiddle(int* a, int left, int right) {
	int middle = (left + right) / 2;
	if (a[left] < a[middle]) {
		if (a[left] < a[middle]) {
			return middle;
		}
		else if (a[left] > a[right]) {
			//此时的middle是最大值
			return left;
		}
		else {
			return right;
		}
	}
	else {
		if (a[middle] > a[right]) {
			return middle;
		}
		else if (a[left] < a[right]) {
			//此时middle最小
			return left;
		}
		else {
			return right;
		}
	}
}
//快速排序之挖坑法
void PartSort2(int* a, int left, int right) {
	int midi = GetMiddle(a, left, right);
	Swap(&a[left], &a[midi]);
	int keyi = a[left];
	int hole = left;
	while (left < right && a[right] >= keyi) {
		//右边先走;将小于keyi的值填入hole中;此时右边就形成了新的坑位;
		--right;
	}
	a[hole] = a[right]; hole = right;
	while (left < right && a[left] <= keyi) {
		//左边走;找大的填入右边的坑位;左边就形成了新的坑位;
		++left;
	}
	a[hole] = a[left]; hole = left; return hole;
}
//快速排序之前后指针法

void QuickSort(int* a, int begin, int rear) {
	if (begin >= rear) {
		return;
	}
	int key = PartSort(a, begin, rear);
	//求时间复杂度:O(N*logN);
	QuickSort(a, begin, key - 1);
	QuickSort(a, key + 1, rear);
}

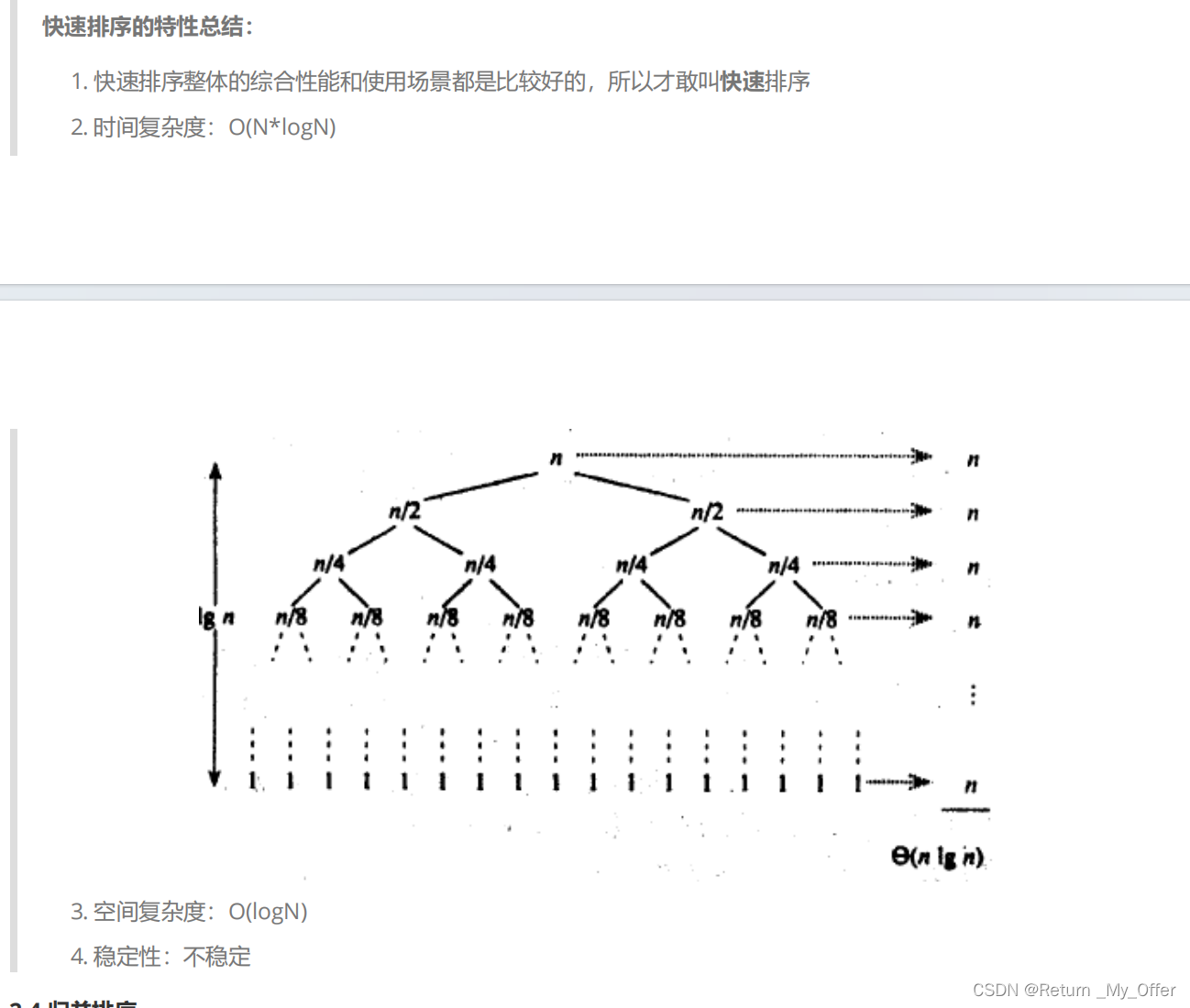
快速排序：采用分治法，选取一个基准元素，将数组分成两个子序列，小于基准元素的放在左边，大于基准元素的放在右边，然后对左右两个子序列递归进行快速排序。时间复杂度为O(nlogn)

void insertion_sort(int arr[], int len) {
    int i, j, temp;
    for (i = 1; i < len; i++) {
        temp = arr[i];
        for (j = i - 1; j >= 0 && arr[j] > temp; j--) {
            arr[j + 1] = arr[j];
        }
        arr[j + 1] = temp;
    }
}

5归并排序

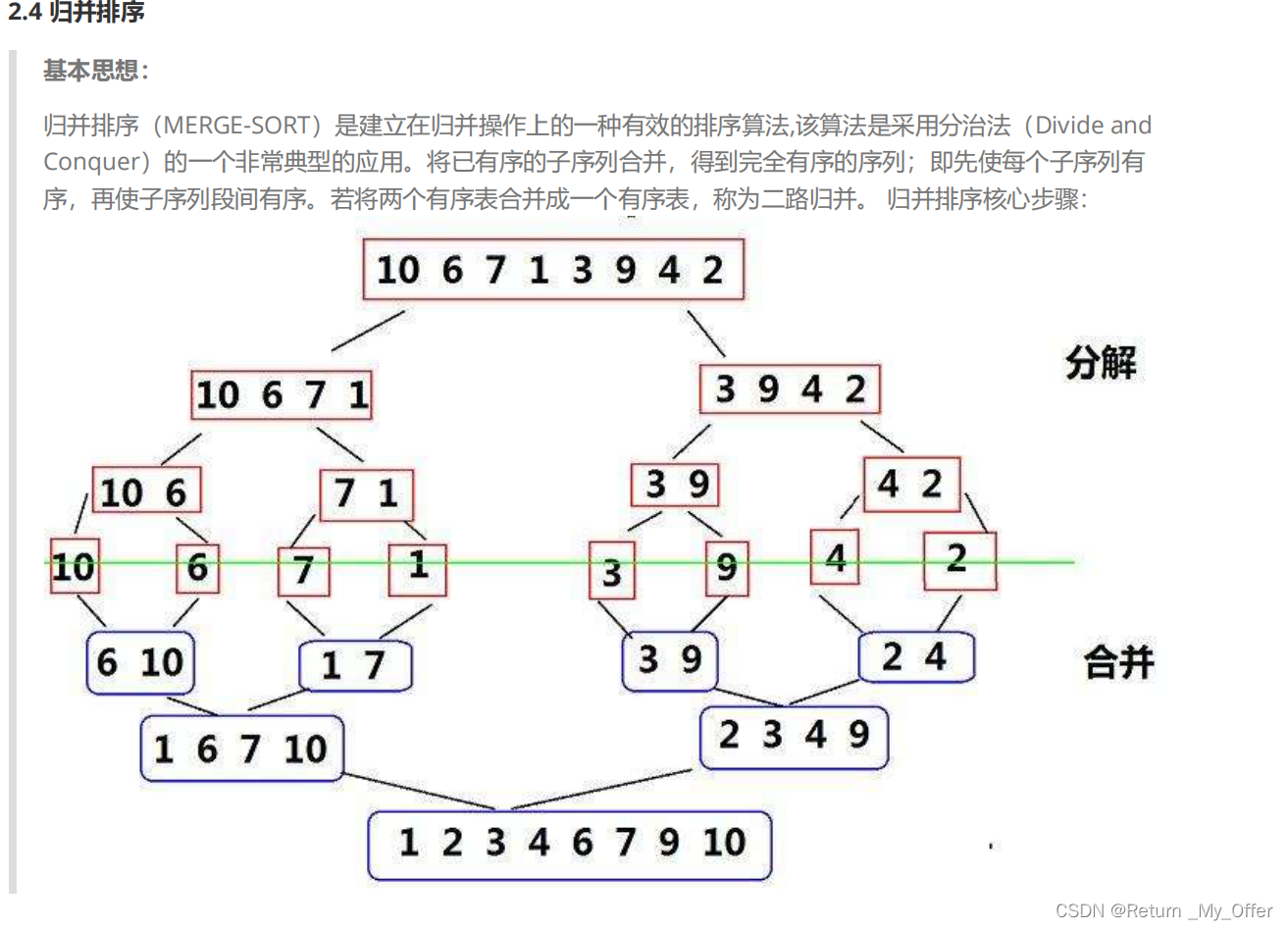
归并排序：采用分治法，将数组分成若干个子序列，对每个子序列进行排序，然后再将已排序的子序列合并成一个有序的序列。时间复杂度为O(nlogn)

void merge(int arr[], int left, int mid, int right) {
    int i = left, j = mid + 1, k = 0;
    int *temp = (int *)malloc((right - left + 1) * sizeof(int));
    while (i <= mid && j <= right) {
        if (arr[i] <= arr[j]) {
            temp[k++] = arr[i++];
        } else {
            temp[k++] = arr[j++];
        }
    }
    while (i <= mid) {
        temp[k++] = arr[i++];
    }
    while (j <= right) {
        temp[k++] = arr[j++];
    }
    for (i = left, k = 0; i <= right; i++, k++) {
        arr[i] = temp[k];
    }
    free(temp);
}

void merge_sort(int arr[], int left, int right) {
    if (left >= right) {
        return;
    }
    int mid = (left + right) / 2;
    merge_sort(arr, left, mid);
    merge_sort(arr, mid + 1, right);
    merge(arr, left, mid, right);
}

6希尔排序

希尔排序：是插入排序的改进版，通过将数组分成若干个子序列进行插入排序，最后再对整个数组进行一次插入排序。时间复杂度为O(nlogn)

//2.希尔排序
void ShellSort(int* a, int n) {
	int gap = 3;
	//2(1).控制整个循环
	for (int j = 0; j < gap; ++j) {
		//2(2).控制一组循环
		for (int i = j; i < n - gap; i += gap) {
			int rear = 0;
			int tmp = a[rear + gap]; while (rear >= 0) {
				if (tmp < a[rear]) {
					a[rear + gap] = a[rear];
					rear -= gap;
				}
				else {
					break;
				}
			}
			a[rear + gap] = tmp;
		}
	}
}