数据结构和算法（11）：红黑树

概述

伸展树实现简便、无需修改节点结构、分摊复杂度低，但可惜最坏情况下的单次操作需要O(n)时间。
AVL树尽管可以保证最坏情况下的单次操作速度，但需在节点中嵌入平衡因子等标识；更重要的是，删除操作之后的重平衡可能需做多达O(logn)次旋转，从而频繁地导致全树整体拓扑结构的大幅度变化。

红黑树通过为节点指定颜色，并巧妙地动态调整，红黑树可保证：在每次插入或删除操作之后的重平衡过程中，全树拓扑结构的更新仅涉及常数个节点。尽管最坏情况下需对多达O(logn)个节点重染色，但就分摊意义而言仅为O(1)个。

在AVL树“适度平衡”标准的基础上，进一步放宽条件：任一节点左、右子树的高度，相差不得超过两倍。

接口和定义

统一地引入n + 1个外部节点，以保证原树中每一节点（现称作内部节点，白色八角形）的左、右孩子均非空——尽管有可能其中之一甚至二者同时是外部节点。当然，这些外部节点的引入只是假想式的，在具体实现时并不一定需要兑现为真实的节点。
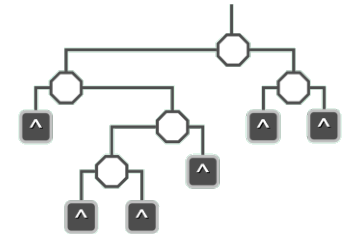
在这里插入图片描述

定义

由红、黑两色节点组成的二叉搜索树若满足以下条件，即为红黑树（red-black tree）：
(1) 树根始终为黑色；
(2) 外部节点均为黑色；
(3) 其余节点若为红色，则其孩子节点必为黑色；
(4) 从任一外部节点到根节点的沿途，黑节点的数目相等。

条件(1)和(2)意味着红节点均为内部节点，且其父节点及左、右孩子必然存在。另外，条件(3)意味着红节点之父必为黑色，因此树中任一通路都不含相邻的红节点。
在从根节点通往任一节点的沿途，黑节点都不少于红节点。除去根节点本身，沿途所经黑节点的总数称作该节点的黑深度（black depth）——根节点的黑深度为0，其余依此类推。故条件(4)亦可等效地理解和描述为“所有外部节点的黑深度统一”

除去（黑色）外部节点，沿途所经黑节点的总数称作该节点的黑高度（black height）。如此，所有外部节点的黑高度均为0，其余依此类推。

根节点的黑高度亦称作全树的黑高度，在数值上与外部节点的黑深度相等。

（2,4）树

在红黑树与4阶B-树之间，存在极其密切的联系；经适当转换之后，二者相互等价！

具体地，自顶而下逐层考查红黑树各节点：每遇到一个红节点，都将对应的子树整体提升一层，从而与其父节点（必黑）水平对齐，二者之间的联边则相应地调整为横向。
如此转换之后，横向边或向左或向右，但由红黑树的条件(3)，同向者彼此不会相邻；即便不考虑联边的左右方向，沿水平方向相邻的边至多两条（向左、右各一条），涉及的节点至多三个（一个黑节点加上零到两个红节点）。此时，若将原红黑树的节点视作关键码，沿水平方向相邻的每一组（父子至多三个）节点即恰好构成4阶B-树的一个节点。

在这里插入图片描述
(2,4)-树中的每个节点应包含且仅包含一个黑关键码，同时红关键码不得超过两个。而且，若某个节点果真包含两个红关键码，则黑关键码的位置必然居中。

平衡性

红黑树的黑高度不低二高度的一半；反之，高度不超过黑高度的两倍。
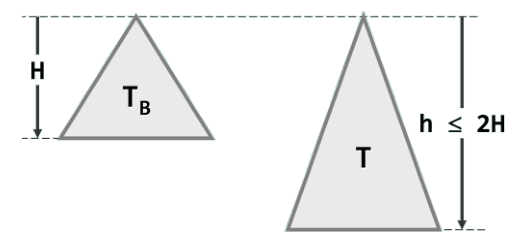
在这里插入图片描述
红黑树的性能首先取决于其平衡性。

含n个内部节点的红黑树T的高度h也不致超过O(logn)： $\log_2(n+1)\leq h \leq 2 \cdot \log_2(n+1)$
尽管红黑树不能如完全树那样可做到理想平衡，也不如AVL树那样可做到较严格的适度平衡，但其高度仍控制在最小高度的两倍以内，渐进的角度看仍是O(logn)，依然保证了适度平衡。

#include "../BST/BST.h”	//基于BST实现RedBlack
template <typename T> class RedBlack : public BST<T> { 	//RedBlack树模板类
protected:
	void solveDoubleRed ( BinNodePosi(T) x );	//双红修正
	void solveDoubleBlack ( BinNodePosi(T) x );	//双黑修正
	int updateHeight ( BinNodePosi(T) x );		//更新节点x的高度
public:
	BinNodePosi(T) insert ( const T&e );	//插入（重写)
	bool remove ( const T&e );	//删除（重写)
//BST::search()等其余接口可直接沿用
};

节点插入算法

经调用接口search(e)做查找之后，确认目标节点尚不存在。
于是，在查找终止的位置x处创建节点，并随即将其染成红色（除非此时全树仅含一个节点）。
现在，对照红黑树的四项条件，唯有(3)未必满足——亦即，此时x的父亲也可能是红色。

红黑树insert()接口

template 〈typename T> BinNodePosi(T) RedBlack<T>::insert ( const T& e ) { //将e插入红黑树
	BinNodePosi(T) & x = search ( e ); if ( x ) return x;		//确认目标不存在（留意对_hot的设置)
	x = new BinNode<T> ( e，_hot，NULL，NULL， -1 ); _size++;	//创建红节点x︰以_hot为父，黑高度-1
	solveDoubleRed ( x ); return x ? x : _hot->parent;			//经双红修正后，即可返回
}	//无论e是否存在于原树中，返回时总有x->data == e

因新节点的引入，而导致父子节点同为红色的此类情况，称作双红。
调用solveDoubleRed(x)接口。每引入一个关键码，该接口都可能迭代地调用多次。在此过程中，当前节点x的兄弟及两个孩子（初始时都是外部节点），始终均为黑色。
将x的父亲与祖父分别记作p和g。既然此前的红黑树合法，故作为红节点p的父亲，g必然存在且为黑色。g作为内部节点，其另一孩子（即p的兄弟、x的叔父）也必然存在，将其记作u。

视节点u的颜色不同，分两类情况分别处置：
1.双红修正（RR-1）
考查u为黑色的情况。此时，x的兄弟、两个孩子的黑高度，均与u相等。
图(a)和(b)为此类情况的两种可能：
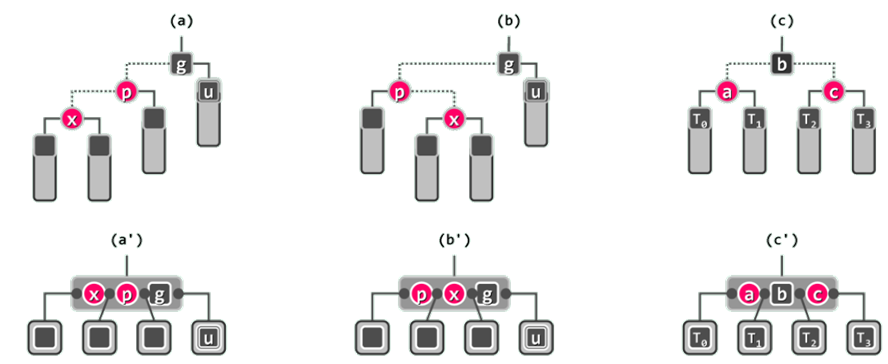在这里插入图片描述此时红黑树条件(3)的违反，从B-树角度等效地看，即同一节点不应包含紧邻的红色关键码。如图(c’)所示，只需令黑色关键码与紧邻的红色关键码互换颜色。从图©红黑树的角度看，这等效于按中序遍历次序，对节点x、p和g及其四棵子树，做一次局部“3 + 4”重构。

如此调整之后，局部子树的黑高度将复原，这意味着全树的平衡也必然得以恢复。
同时，新子树的根节点b为黑色，也不致引发新的双红现象。至此，整个插入操作遂告完成

2.双红修正（RR-2 ）
再考查节点u为红色的情况。此时，u的左、右孩子非空且均为黑色，其黑高度必与x的兄弟以及两个孩子相等。
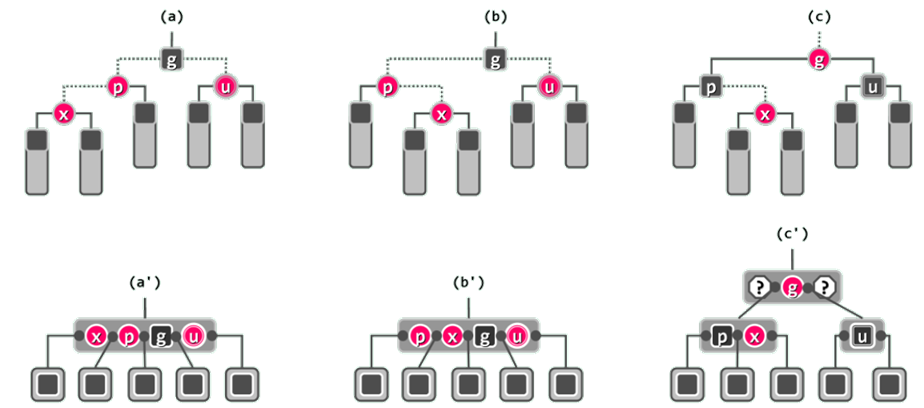在这里插入图片描述上方、下方分别为红黑树及其对应B-树的局部

图(a)和(b)给出了两种可能的此类情况。此时红黑树条件(3)的违反，从B-树角度等效地看，即该节点因超过4度而发生上溢。
从图©红黑树的角度来看，只需将红节点p和u转为黑色，黑节点g转为红色，x保持红色。从图(c’)B-树的角度来看，等效于上溢节点的一次分裂。
如此调整之后局部子树的黑高度复原。然而，子树根节点g转为红色之后，有可能在更高层再次引发双红现象。
从图(c’)B-树的角度来看，对应于在关键码g被移出并归入上层节点之后，进而导致上层节点的上溢——即上溢的向上传播。
若果真如此，可以等效地将g视作新插入的节点，同样地分以上两类情况如法处置。每经过一次这样的迭代，节点g都将在B-树中（作为关键码）上升一层，而在红黑树中存在双红缺陷的位置也将相应地上升两层，故累计至多迭代O(logn)次。
若最后一步迭代之后导致原树根的分裂，并由g独立地构成新的树根节点，则应遵照红黑树条件(1)的要求，强行将其转为黑色——如此，全树的黑高度随即增加一层。

双红修正的复杂度

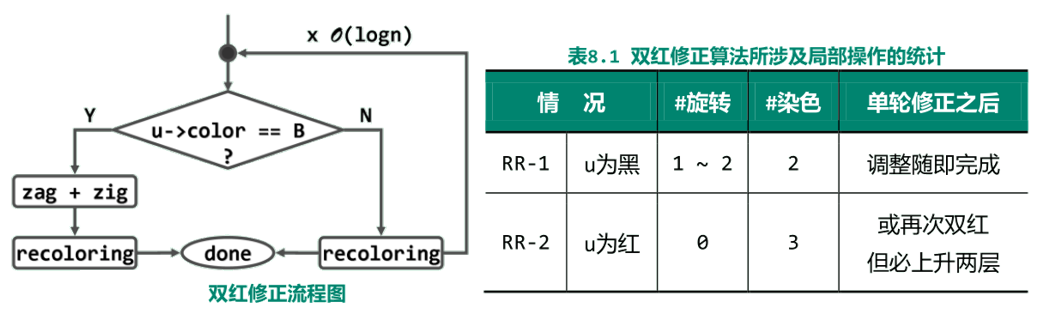在这里插入图片描述对于前一种情况，只需做一轮修正；
后一种情况虽有可能需要反复修正，但由于修正位置的高度会严格单调上升，故总共也不过O(logn)轮。
每一轮修正只涉及到常数次的节点旋转或染色操作。因此，节点插入之后的双红修正，累计耗时不会超过O(logn)。即便计入此前的关键码查找以及节点接入等操作，红黑树的每次节点插入操作，都可在O(logn)时间内完成。

只有在RR-1修复时才需做1~2次旋转；而且一旦旋转后，修复过程必然随即完成。故就全树拓扑结构而言，每次插入后仅涉及常数次调整；而且稍后将会看到，红黑树的节点删除操作亦是如此。

实现

//*RedBlack双红调整算法︰解决节点x与其父均为红色的问题。分为两大类情况︰
//*RR-1∶2次颜色翻转，2次黑高度更新，1~2次旋转，不再递归
//*RR-2∶3次颜色翻转，3次黑高度更新，0次旋转，需要递归

template <typename T> void RedBlackT>: :solveDoubleRed ( BinNodePosi(T) x ) {	//x当前必为红
	if ( IsRoot ( *x ) )//若已（递归）转至树根，则将其转黑，整树黑高度也随之递增
		{ _root->color = RB_BLACK; _root->height++; return; }	//否则，x的父亲p必存在
	BinNodePosi(T) p = x->parent; if ( IsBlack ( p ) ) return;	//若p为黑，则可终止调整。否则			
	BinNodePosi(T) g = p->parent;	//既然p为红，则x的祖父必存在，且必为黑色
	BinNodePosi(T) u = uncle ( x );	//以下，视x叔父u的颜色分别处理
	if ( IsBlack ( u ) ) { //u为黑色（含NULL)时
		if ( IsLChild ( *x ) == IsLChild ( *p ))//若x与p同侧(即zIg-zIg或zAg-zAg )，则
			p->color = RB_BLACK;	//p由红转黑，x保持红
		else 	//若x与p异侧(即zIg-zAg或zAg-zIg )，则
			x->color = RB_BLACK;//x由红转黑，p保持红
		g->color = RB_RED; //g必定由黑转红
//以上虽保证总共两次染色，但因增加了判断而得不偿失
//在旋转后将根置黑、孩子置红，虽需三次染色但效率更高
		BinNodePosi(T) gg = g->parent;	//曾祖父( great-grand parent )
		BinNodePosi(T) r = FromParentTo ( *g ) = rotateAt ( x );	//调整后的子树根节点
		r->parent = gg; //与原曾祖父联接
	}else { //若u为红色
		p->color = RB_BLACK; p->height++; 	//p由红转黑
		u->color = RB_BLACK; u->height++;	//u由红转黑
		if ( !IsRoot ( *g ) ) g->color = RB_RED;	//g若非根，则转红
		solveDoubleRed ( g );	//继续调整g（类似于尾递归，可优化为迭代形式)
	}
}

节点删除算法

接口

template <typename T> bool RedBlack<T>::remove ( const T& e ) {//从红黑树中删除关键码e
	BinNodePosi(T)& x = search ( e ); if ( !x ) return false;//确认目标存在（留意_hot的设置)
	BinNodePosi(T) r = removeAt ( x,_hot ); if ( ! ( --_size ) ) return true;//实施删除
// assert: _hot某一孩子刚被删除，且被r所指节点（可能是NULL)接替。以下检查是否失衡，并做必要调整
	if ( ! _hot )//若刚被删除的是根节点，则将其置黑，并更新黑高度
		{ _root->color = RB_BLACK; updateHeight ( _root ); return true; }
//assert:以下，原x(现r)必非根，_hot必非空
	if ( BlackHeightUpdated ( *_hot ) ) return true;	//若所有祖先的黑深度依然平衡，则无需调整
	if ( IsRed ( r ) )	//否则，若r为红，则只需令其转黑
		{ r->color = RB_BLACK; r->height++; return true; }
//assert:以下，原x(现r)均为黑色
	solveDoubleBlack ( r ); return true;	//经双黑调整后返回
}//若目标节点存在且被删除，返回true;否则返回false

首先调用标准接口BST::search(e)，查找目标节点x。若查找成功，则调用内部接口removeAt(x)实施删除。其间无论是否做过一次节点交换，均以r指向实际被删除节点x的接替者，p = _hot为其父亲。
此时红黑树的前两个条件继续满足，但后两个条件却未必依然满足。

除了其接替者r，x 还应有另一个孩子w。既然x是实际被删除者，故 w 必为（黑色的）外部节点 NULL。
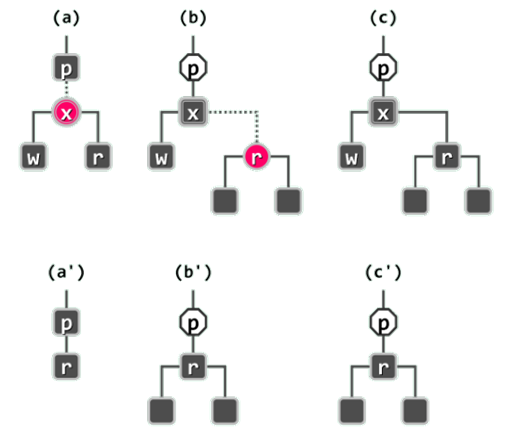
在这里插入图片描述
如图 (a) 和 (a’) 所示，若 x 为红色，则在删除x并代之以r后，条件(3~4)依然满足；反之，若x为黑色，则要看其替代者r的颜色。
如图 (b) 和 (b’) 所示，若 r 为红色，则只需将其翻转为黑色，即可使条件(3~4)重新满足。
如图 ( c) 和 (c’) 所示，若 x 和 r 均为黑色，则为使条件(3~4)重新成立，还需要做略微复杂一些的处理。
因某一无红色孩子的黑节点被删除，而导致的此类复杂情况，称作双黑（double black）现象。此时，需从r出发调用solveDoubleBlack(r)算法予以修正。
自然，原黑节点x的兄弟必然非空，将其记作s；x的父亲记作p，其颜色不确定（故在图中以八角形示意）。

视s和p颜色的不同组合，按四种情况分别处置：

1.双黑修正（BB-1）
节点x的另一孩子w = NULL，故从B-树角度 (a’) 看节点x被删除之后的情况，可以等效地理解为：关键码x原所属的节点发生下溢；此时，t和s必然属于B-树的同一节点，且该节点就是下溢节点的兄弟。故可参照B-树的调整方法，下溢节点从父节点借出一个关键码（p），然后父节点从向下溢节点的兄弟节点借出一个关键码（s），调整后的效果如图(b')。
在这里插入图片描述
从红黑树的角度 （图(b)） 来看，上述调整过程等效于，对节点t、s和p实施 “3 + 4”重构。
若这三个节点按中序遍历次序重命名为a、b和c，则还需将a和c染成黑色，b则继承p此前的颜色。
将t和p染成黑色，s继承p此前的颜色。整个过程中节点r保持黑色不变。
经以上处理之后，红黑树的所有条件，都在这一局部以及全局得到恢复，故删除操作遂告完成。

2.双黑修正（BB-2-R）
节点s及其两个孩子均为黑色时，视节点p颜色的不同，又可进一步分为两种情况。

与BB-1类似，在对应的B-树中，关键码x的删除导致其所属的节点下溢。但因此时关键码s所在节点只有两个分支，故下溢节点无法从父节点借出关键码（p）。
在这里插入图片描述
如图(b’) 所示，将关键码p取出并下降一层，然后以之为“粘合剂”，将原左、右孩子合并为一个节点。从红黑树角度看，这
一过程可如 图(b) 所示等效地理解为：s和p颜色互换。

经过以上处理，红黑树的所有条件都在此局部得以恢复。另外，由于关键码p原为红色，故如 图(a’) 所示，在关键码p所属节点中，其左或右必然还有一个黑色关键码（当然，不可能左、右兼有）——这意味着，在关键码p从其中取出之后，不致引发新的下溢。至此，红黑树条件亦必在全局得以恢复，删除操作即告完成。

3.双黑修正（BB-2-B ）
考虑节点s、s的两个孩子以及节点p均为黑色的情况。
在这里插入图片描述
与BB-2-R类似，在对应的B-树中，因关键码x的删除，导致其所属节点发生下溢。
如 图(b’) 所示，将下溢节点与其兄弟合并。从红黑树的角度来看，这一过程可如图(b)所示等效地理解为：节点s由黑转红。
由 图(b) 可知，经以上处理，红黑树所有条件都在此局部得到恢复。
因s和x在此之前均为黑色，故如 图(a’) 所示，p原所属的B-树节点必然仅含p这一个关键码。于是在p被借出之后，该节点必将继而发生下溢，故有待于后续进一步修正。
此时的状态可等效地理解为：节点p的父节点刚被删除。
这是双黑修正过程中，需要再次迭代的唯一可能。幸运的是，尽管此类情况可能持续发生，下溢的位置也必然不断上升，故至多迭代O(logn)次后必然终止。

4.双黑修正（BB-3 ）

在这里插入图片描述
考虑节点s为红色的情况。
如 图(a) 所示，即为一种典型的此类情况。此时，作为红节点s的父亲，节点p必为黑色；同时，s的两个孩子也应均为黑色。
从B-树的角度来看，只需 如图(b’) 所示，令关键码s与p互换颜色，即可得到一棵与之完全等价的B-树。而从红黑树的角度来看，这一转换对应于以节点p为轴做一次旋转，并交换节点s与p的颜色。
在转换之后的红黑树中，被删除节点x（及其替代者节点r）有了一个新的兄弟s'——与此前的兄弟s不同，s'必然是黑的！这就意味着，接下来可以套用此前所介绍其它情况的处置方法，继续并最终完成双黑修正。

在这里插入图片描述
同样需要注意：现在的节点p，也已经黑色转为红色。因此接下来即便需要继续调整，必然既不可能转换回此前的情况BB-3，也不可能转入可能需要反复迭代的情况BB-2-B。

复杂度

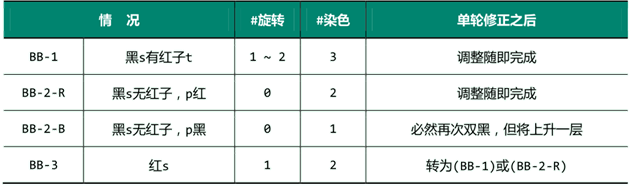
在这里插入图片描述其中涉及的重构、染色等局部操作，均可在常数时间内完成。

在这里插入图片描述
两种情况各自只需做一轮修正，最后一种情况亦不过两轮。
情况BB-2-B虽可能需要反复修正，但由于待修正位置的高度严格单调上升，累计也不致过O(logn)轮，故双黑修正过程总共耗时不超过O(logn)。即便计入此前的关键码查找和节点摘除操作，红黑树的节点删除操作总是可在O(logn)时间内完成。
可以发现： 一旦在某步迭代中做过节点的旋转调整，整个修复过程便会随即完成。 因此与双红修正一样，双黑修正的整个过程，也仅涉及常数次的拓扑结构调整操作。

修正算法的实现

1 /******************************************************************************************
2 * RedBlack双黑调整算法：解决节点x不被其替代的节点均为黑色的问题
3 * 分为三大类共四种情冴：
4 * BB-1 ：2次颜色翻转，2次黑高度更新，1~2次旋转，不再递归
5 * BB-2R：2次颜色翻转，2次黑高度更新，0次旋转，不再递归
6 * BB-2B：1次颜色翻转，1次黑高度更新，0次旋转，需要递归
7 * BB-3 ：2次颜色翻转，2次黑高度更新，1次旋转，转为BB-1或BB2R
8 ******************************************************************************************/

template <typename T> void RedBlack<T>::solveDoubleBlack ( BinNodePosi(T) r ) {
	BinNodePosi(T) p = r ? r->parent : _hot; if ( !p ) return; //r的父亲
	BinNodePosi(T) s = ( r == p->lc ) ? p->rc : p->lc; //r的兄弟
	if ( IsBlack ( s ) ) { //兄弟s为黑
		BinNodePosi(T) t = NULL;//s的红孩子（若左、右孩子皆红，左者优先﹔皆黑时为NULL )
		if( HasLChild ( *s ) &8 IsRed ( s->lc ) ) t = s->lc;
		else if ( HasRChild ( *s ) && IsRed ( s->rc ) ) t = s->rc;
		if ( t ) {//黑s有红孩子︰BB-1
			RBColor oldColor = p->color;//备份原子树根节点p颜色，并对t及其父亲、祖父
			BinNodePosi(T) b = FromParentTo ( *p ) = rotateAt ( t );//重平衡，并将新子树的左、右孩子染黑
			if ( HasLChild ( *b ) ) b->lc->color = RB_BLACK; updateHeight ( b->lc );//左孩子
			if ( HasRChild ( *b ) ) b->rc->color = RB_BLACK; updateHeight ( b->rc ); //右孩子
			b->color = oldcolor; updateHeight ( b );//新子树根节点继承原根节点的颜色
		}else { //黑s无红孩子
			s->color = RB_RED; s->height--; // s转红
			if ( IsRed ( p ) ) { //BB-2R
				p->color = RB_BLACK; //p转黑，但黑高度不变
			}else { //BB-2B
				p->height--; //p保持黑，但黑高度下降
				solveDoubleBlack ( p );
			}
		}
	} else { //兄弟s为红:BB-3
		s->color = RB_BLACK; p->color = RB_RED;//s转黑，p转红
		BinNodePosi(T) t = IsLChild ( *s ) ? s->lc : s->rc; //取t与其父s同侧
		_hot = p; FromParentTo ( *p ) = rotateAt ( t );	//对t及其父亲、祖父做平衡调整
		solveDoubleBlack ( r );	//继续修正r处双黑——此时的p已转红，故后续只能是BB-1或BB-2R
	}
}