hh第一次记录cf。
复盘
ab题目比较清晰,只开了这两题,后面看了下cd,即使开了翻译也看不懂题目是什么意思,最后放弃睡觉了。。
a是一道思维题,翻了下别人写的发现大家写的各不相同hh
b是一道数学题,过程有点繁琐,需要细心。

Problem - A - Codeforces
数学巧思
题意:
仍然是t组测试哈,给定一个数n,问是否有a+b+c=n,a%3,b%3,c%3不为0,如果存在输出yes并输出这三个数,否则输出no。
设a=3k1+d1,b=3k2+d2,c=3k3+d3
显然,d1,d2,d3只能是1或2
那么我们就只需要对余数进行讨论就行了,
比如给定1和2,这两个数当然是满足条件的,只需要(n-3)%3不为0就好了,也就是(n-3)=3*k+1或2(k>=1)
这一个条件不足以涵盖所有情况,也就是只要还需要n-(3*k+1),n-(3*k+2),即覆盖余数为0,1,2这三种情况
#include<bits/stdc++.h>
signed main()
{
int t;
std::cin>>t;
while(t--)
{
int x;
std::cin>>x;
if((x-3)%3&&(x-3)!=1&&(x-3)!=2&&(x-3)>0)
{
std::cout<<"YES"<<'\n'<<"1 2 "<<x-3<<'\n';
continue;
}
if((x-5)%3&&(x-5)!=1&&(x-5)!=4&&(x-5)>0)
{
std::cout<<"YES"<<'\n'<<"1 4 "<<x-5<<'\n';
continue;
}
if((x-7)%3&&(x-7)!=2&&(x-7)!=5&&(x-7)>0)
{
std::cout<<"YES"<<'\n'<<"2 5 "<<x-7<<'\n';
continue;
}
std::cout<<"NO"<<'\n';
}
return 0;
}但其实经过分析可以发现,只需要上面两个if语句就够了,n-3和n-5已经覆盖了所有情况。
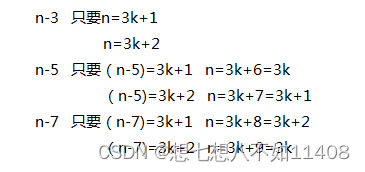
常规循环
因为思路比较简单我就直接复制的别人的代码,枚举前两个数,范围是1-13,然后对n-i-j进行判断就行。
#define ll long long
#include<bits/stdc++.h>
using namespace std;
void solve(){
ll n;cin>>n;
for(ll i=1;i<13;i++){
for(ll j=1;j<13;j++){
ll z=n-i-j;
if(z>0 && i!=j && i!=z && j!=z && i%3!=0 && j%3!=0 && z%3!=0){
cout<<"Yes"<<"\n";
cout<<i<<" "<<j<<" "<<z<<"\n";
return;
}
}
}
cout<<"No"<<"\n";
}
int main(){
ll n;cin>>n;
while(n--)solve();
}Problem - B - Codeforces
题目仍然是t个测试点
题目给出三个点p,a,b,要求以a和b分别为圆心,以w为半径做两个圆
要求o到p在圆上有路
思路分析:
#include<bits/stdc++.h>
using namespace std;
int dis(int x1,int y1,int x2,int y2)
{
return (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);
}
signed main()
{
int t;
std::cin>>t;
while(t--)
{
int p1,p2;
int x1,y1;
int x2,y2;
std::cin>>p1>>p2>>x1>>y1>>x2>>y2;
//只要源点和p都在圆上
//
double s1=min(max(dis(p1,p2,x1,y1),dis(0,0,x1,y1)),
max(dis(p1,p2,x2,y2),dis(0,0,x2,y2)));
double hh=(double)dis(x1,y1,x2,y2)/4;
double s2=max(hh,
(double)min(max(dis(p1,p2,x1,y1),dis(0,0,x2,y2) ),
max(dis(p1,p2,x2,y2),dis(0,0,x1,y1))
)
);
double d=min(s1,s2);
d=sqrt(d);
printf("%.10f\n",d);
}
return 0;
}