数据结构中的树与二叉树,是在建立非线性数据结构方面极为重要的两个概念。它们不仅能够模拟出生活中各种实际问题的复杂关系,还常被用于实现搜索、排序、查找等算法,甚至成为一些大型软件和系统中的基础设施。
无论你是初学者还是进阶者,本文将为你提供简单易懂、实用可行的知识点,帮助你更好地掌握树和二叉树在数据结构和算法中的重要性,进而提升算法解题的能力。接下来让我们开启数据结构与算法的奇妙之旅吧。
目录
二叉树的线索化
堆的定义及其建立
树与森林
霍(哈)夫曼树
二叉树的线索化
线索化二叉树(Threaded Binary Tree)是一种对二叉树进行改造的方法,使得二叉树的遍历更加高效。在线索化二叉树中,除了存储左右子节点的指针外,还存储了一些额外的线索信息,用于快速定位前驱和后继节点。
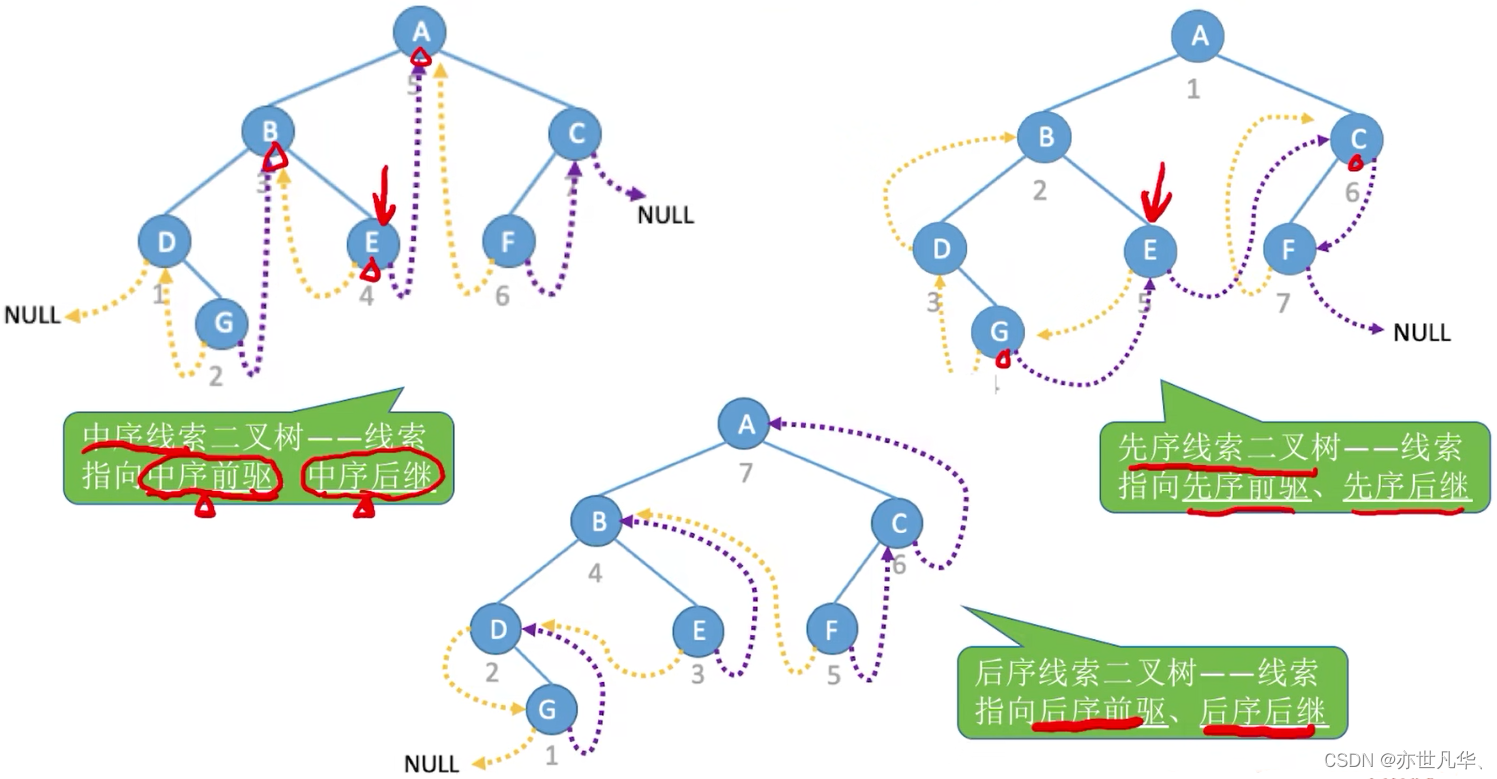
中序线索化二叉树:将二叉树的空指针域利用起来,指向该节点的中序遍历的前驱节点和后继节点。

中序线索二叉树的存储:

先序线索化二叉树:将二叉树的空指针域利用起来,指向该节点的中序遍历的前驱节点和后继节点。

先序线索二叉树的存储:

后序线索化二叉树:将二叉树的空指针域利用起来,指向该节点的中序遍历的前驱节点和后继节点。

先序线索二叉树的存储:

下面是使用C语言实现先序、中序、后续线索化的代码示例:
#include <stdio.h>
#include <stdlib.h>
// 定义二叉树节点结构
typedef struct Node {
int data;
struct Node* left;
struct Node* right;
int isThreaded; // 标志位,用于线索化
} Node;
// 创建新节点
Node* createNode(int data) {
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->data = data;
newNode->left = NULL;
newNode->right = NULL;
newNode->isThreaded = 0;
return newNode;
}
// 先序线索化
void preorderThreading(Node* root, Node** prev) {
if (root == NULL) {
return;
}
if (*prev != NULL && (*prev)->right == NULL) {
(*prev)->right = root; // 将前驱节点的右指针指向当前节点
(*prev)->isThreaded = 1; // 将前驱节点的线索标志位置为1
}
if (root->left == NULL) {
root->left = *prev; // 将当前节点的左指针指向前驱节点
root->isThreaded = 1; // 将当前节点的线索标志位置为1
}
*prev = root;
if (!root->isThreaded) {
preorderThreading(root->left, prev);
}
preorderThreading(root->right, prev);
}
// 中序线索化
void inorderThreading(Node* root, Node** prev) {
if (root == NULL) {
return;
}
inorderThreading(root->left, prev);
if (*prev != NULL && (*prev)->right == NULL) {
(*prev)->right = root; // 将前驱节点的右指针指向当前节点
(*prev)->isThreaded = 1; // 将前驱节点的线索标志位置为1
}
if (root->left == NULL) {
root->left = *prev; // 将当前节点的左指针指向前驱节点
root->isThreaded = 1; // 将当前节点的线索标志位置为1
}
*prev = root;
inorderThreading(root->right, prev);
}
// 后续线索化
void postorderThreading(Node* root, Node** prev) {
if (root == NULL) {
return;
}
postorderThreading(root->left, prev);
postorderThreading(root->right, prev);
if (*prev != NULL && (*prev)->right == NULL) {
(*prev)->right = root; // 将前驱节点的右指针指向当前节点
(*prev)->isThreaded = 1; // 将前驱节点的线索标志位置为1
}
if (root->left == NULL) {
root->left = *prev; // 将当前节点的左指针指向前驱节点
root->isThreaded = 1; // 将当前节点的线索标志位置为1
}
*prev = root;
}
int main() {
// 创建二叉树
Node* root = createNode(1);
root->left = createNode(2);
root->right = createNode(3);
root->left->left = createNode(4);
root->left->right = createNode(5);
// 先序线索化
Node* prev = NULL;
preorderThreading(root, &prev);
// 中序线索化
prev = NULL;
inorderThreading(root, &prev);
// 后续线索化
prev = NULL;
postorderThreading(root, &prev);
return 0;
}回顾重点,其主要内容整理成如下内容:

堆的定义及其建立
堆是一种特殊的完全二叉树,它具有以下两个特性:
1)堆中任意节点的值都必须满足堆的性质:对于大根堆(或最大堆),每个节点的值都大于等于其子节点的值;对于小根堆(或最小堆),每个节点的值都小于等于其子节点的值。
2)堆中的二叉树总是完全填满的,即除了最后一层,其他层都是满的,且最后一层从左到右连续。
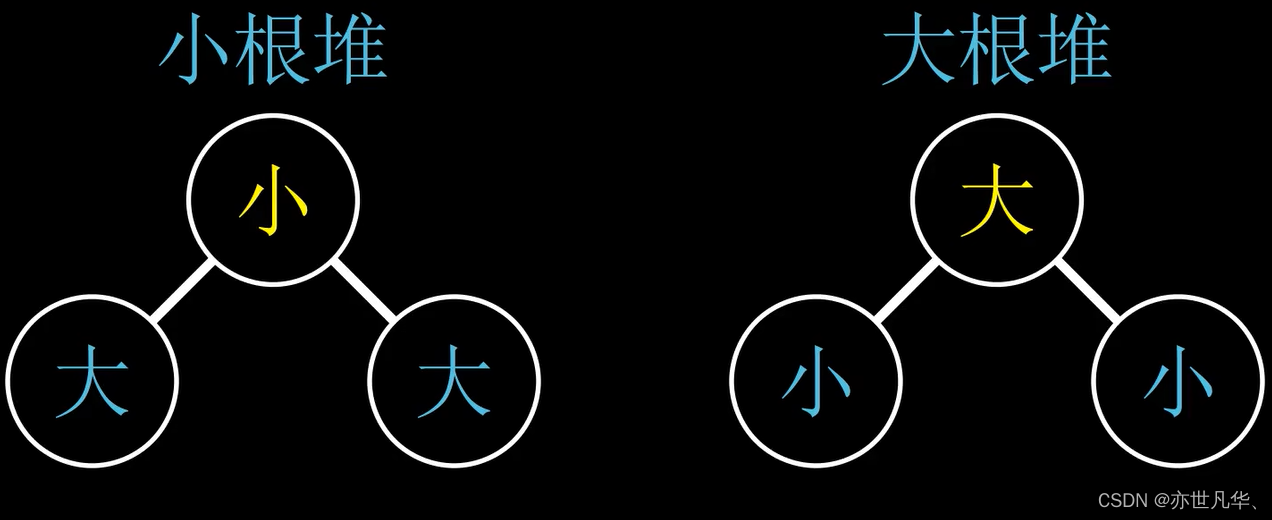
举个例子:

一个堆可以用一个一维数组来描述:
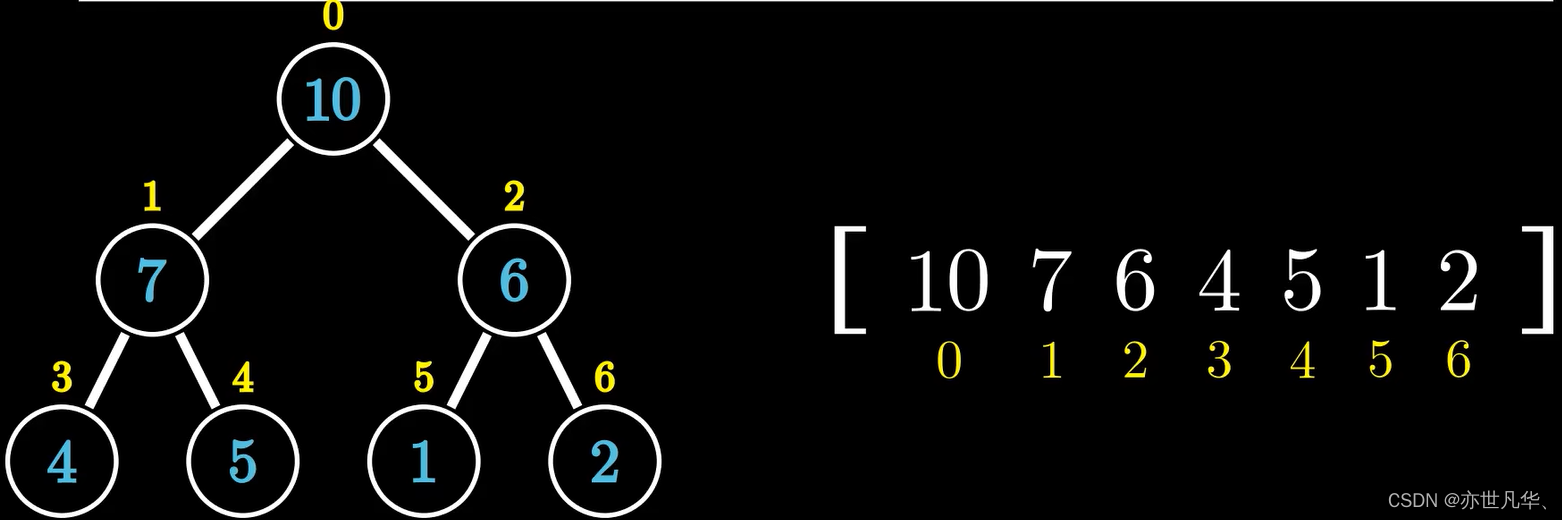
自顶向下建堆法:方法通过插入堆然后通过上滤方式(下与上比较,下比上大,下与上互换位置):

自下而上建堆法:方法是对每个父结点进行下滤(上与下比较,上比下大,上与下互换位置):

树与森林
树的存储表示:
双亲表示法(顺序存储):用一个一维数组来存储树的所有节点,同时利用另外一个一维数组来存储每个节点的双亲节点。使用顺序存储双亲表示法时,可以方便地通过节点的下标查找其双亲节点,也可以根据节点的双亲节点编号快速查找该节点在数组中的位置。但是,插入和删除操作相对较为复杂,需要进行元素的移动,而且相比链式存储,需要额外的空间存储双亲节点编号信息。

如果想增一个数据结点,我们只需要在空白的位置写入这个结点,并且记录其与双亲结点的关系:

如果想删除一个结点可以采用以下两种方式。
方案一:删除的元素的双亲结点设为-1,表示该位置是空的
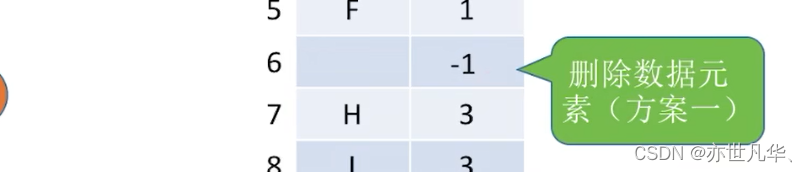
方案二:把尾部的元素填充到删除的结点上面:

如果删除的是一个父结点,需要查找其下面所有子孙节点并全部删除,如果之前采用过方案一的方式的话会导致会多遍历一个空数据从而导致遍历的速度变慢:

孩子表示法(顺序+链式存储):使用顺序存储孩子表示法时,可以通过节点的指针或索引直接访问其孩子节点,不需要遍历整个数组。对于叶子节点,可以使用特殊值(如-1)表示没有孩子节点。相比于双亲表示法,顺序存储孩子表示法节省了存储空间。
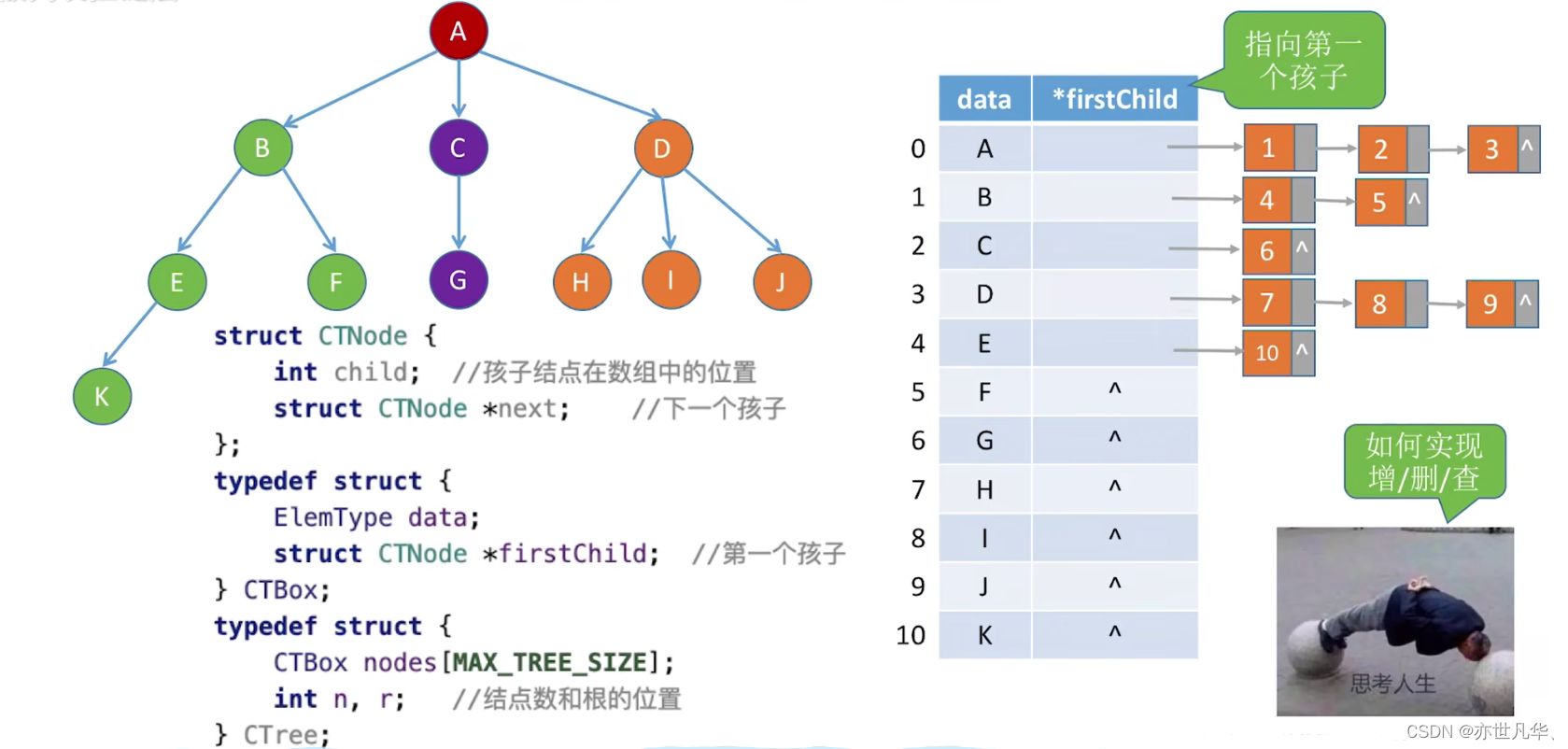
孩子兄弟表示法(链式存储): 孩子兄弟表示法适用于表示一般的树结构,而不仅限于二叉树。它节省了存储空间,并提供了一种紧凑且高效的方式来表示树。这种表示法常用于一些树的应用,如表达式树、文件系统的目录结构等。同时,由于链式结构的特性,插入和删除节点也相对较容易。

树和二叉树的相互转化:
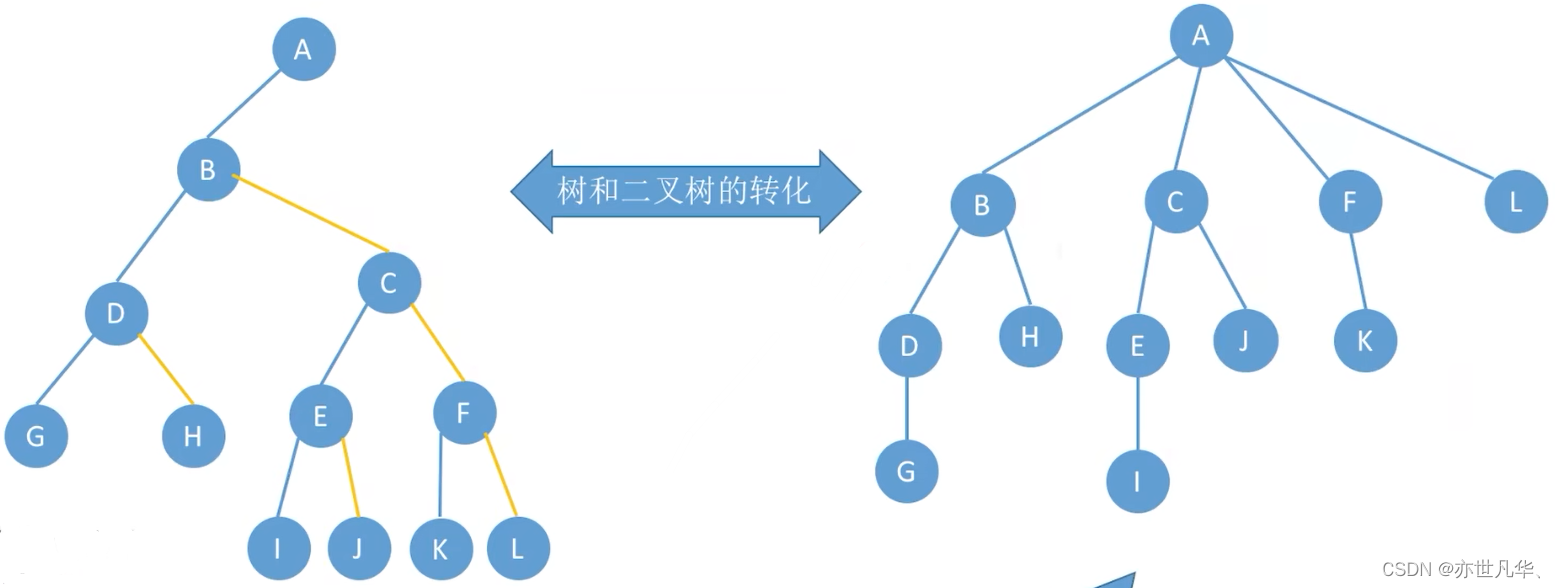
森林与二叉树的转换:
森林转换为二叉树的方式:左序列是父子关系、右序列是兄弟关系。具体转换如下:
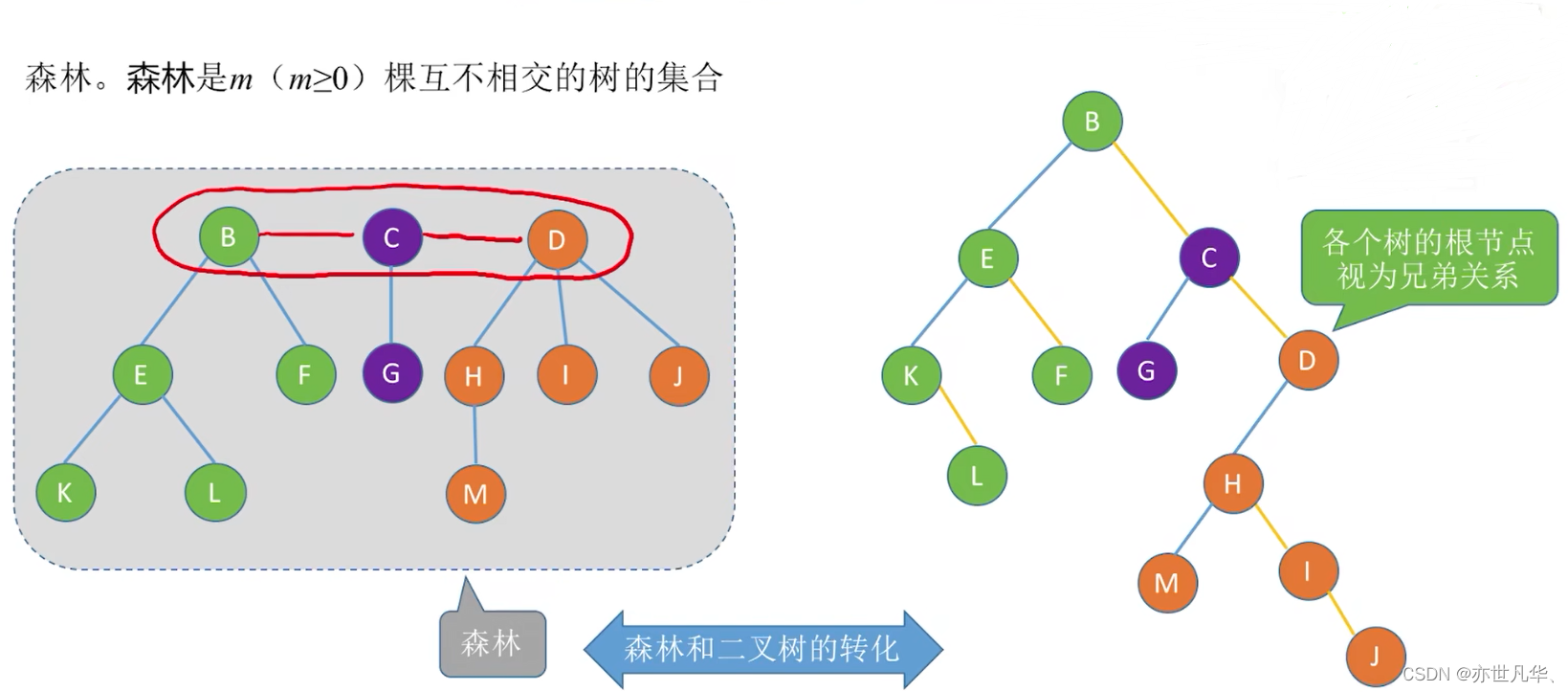
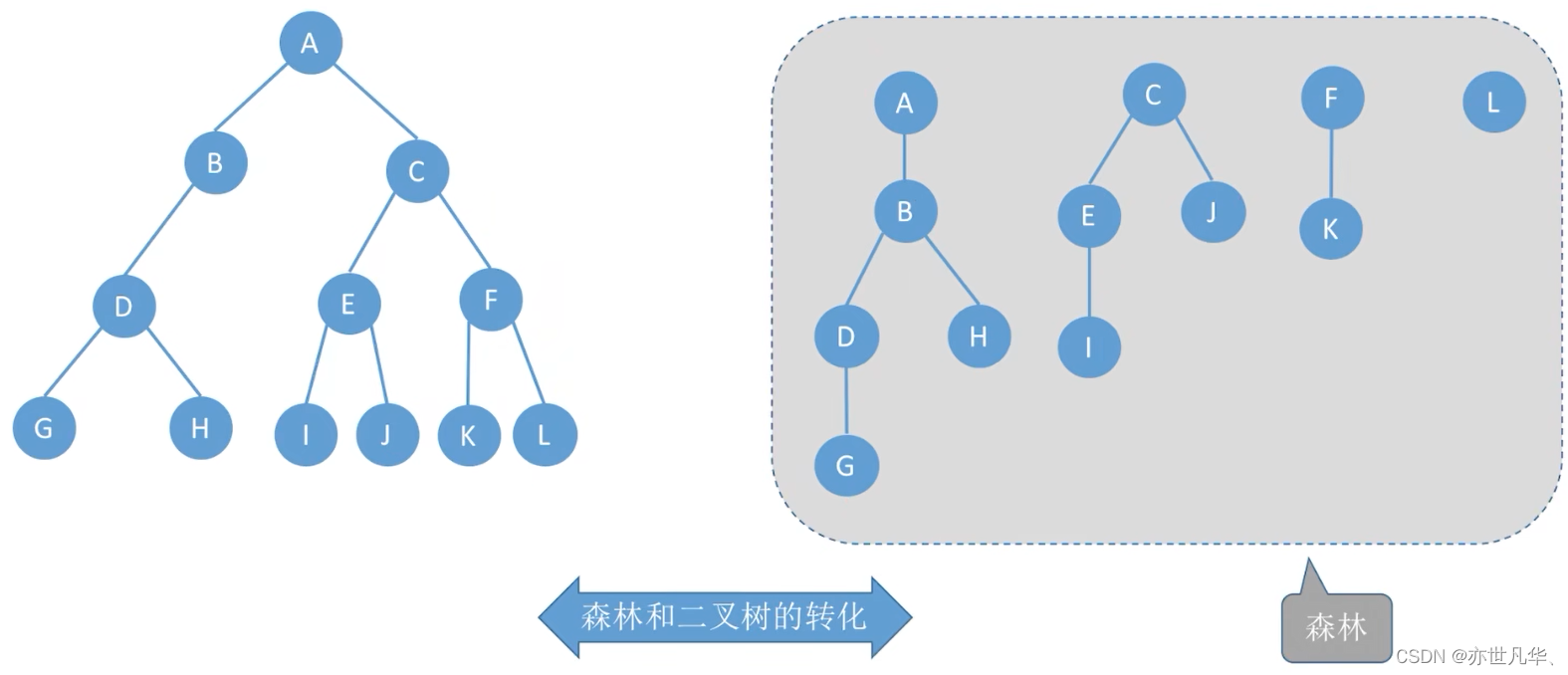
回顾重点,其主要内容整理成如下内容:
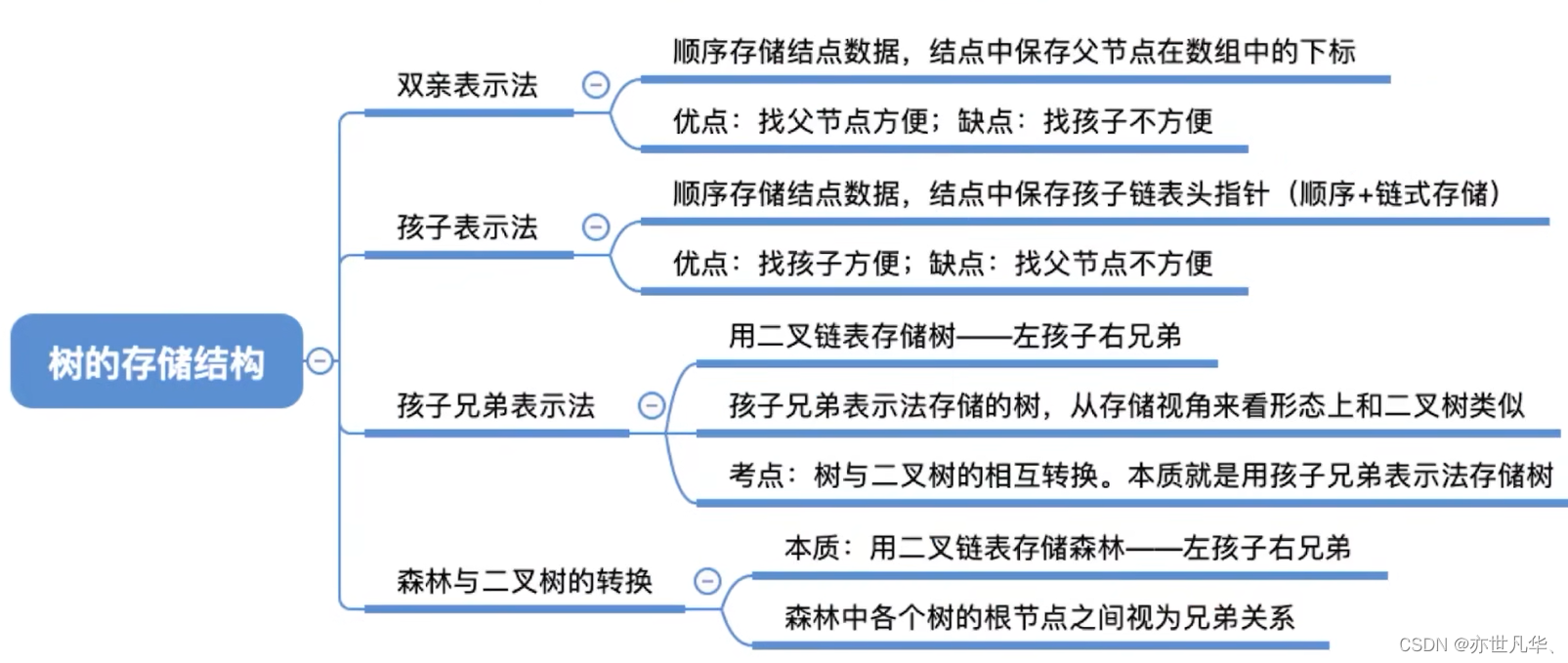
树和森林的遍历:
树的先根遍历:
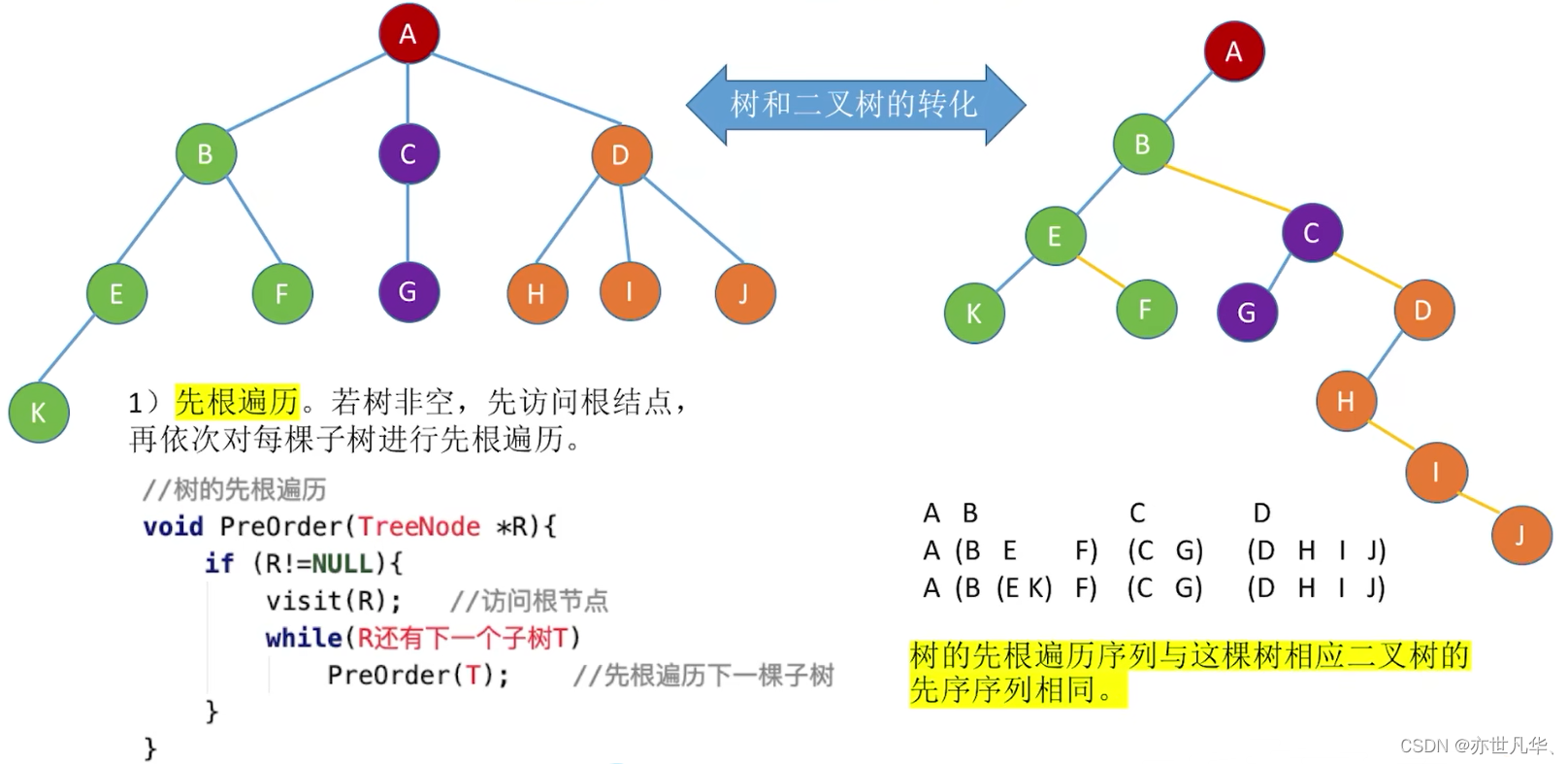
树的后根遍历:

树的层次遍历:
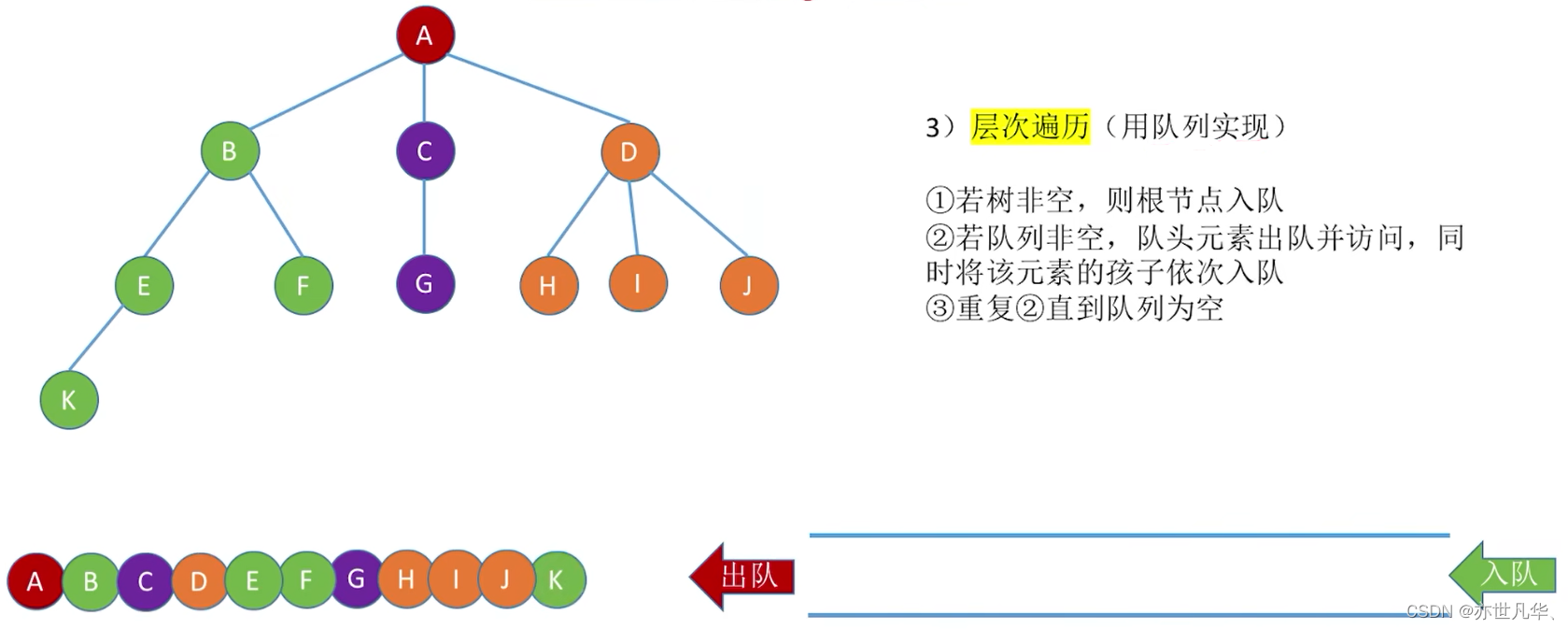
森林的先序遍历:

森林的中序遍历:
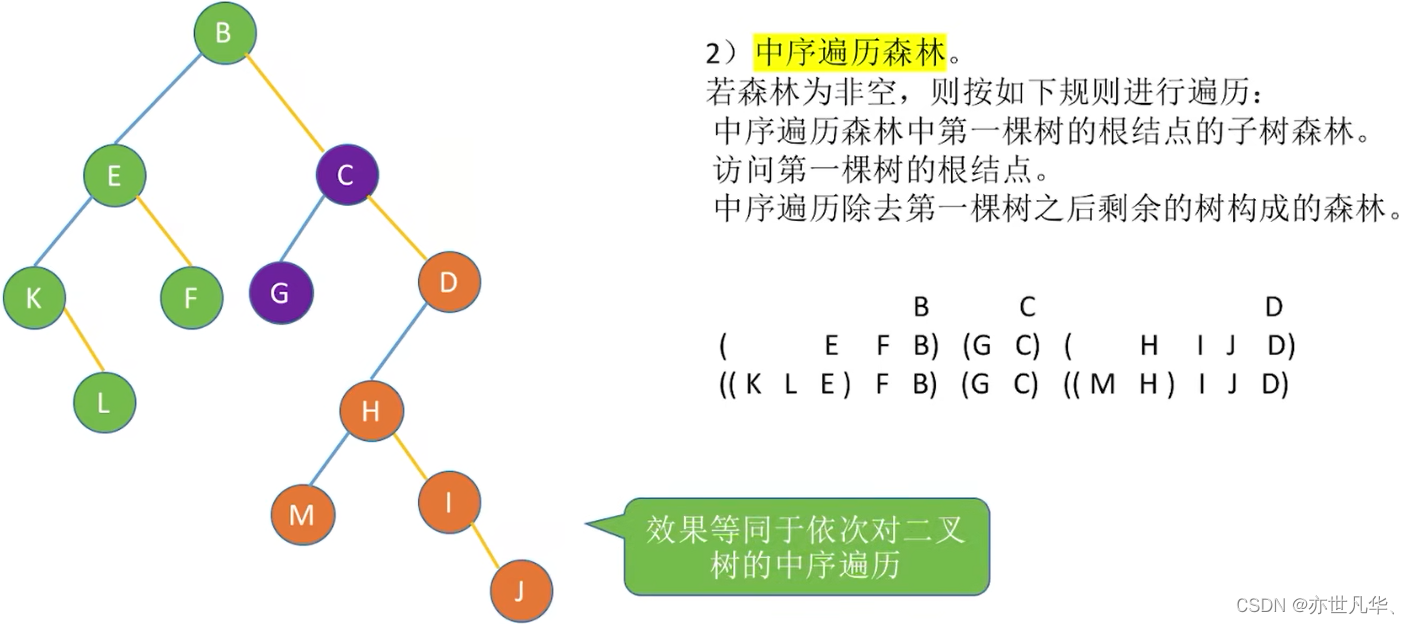
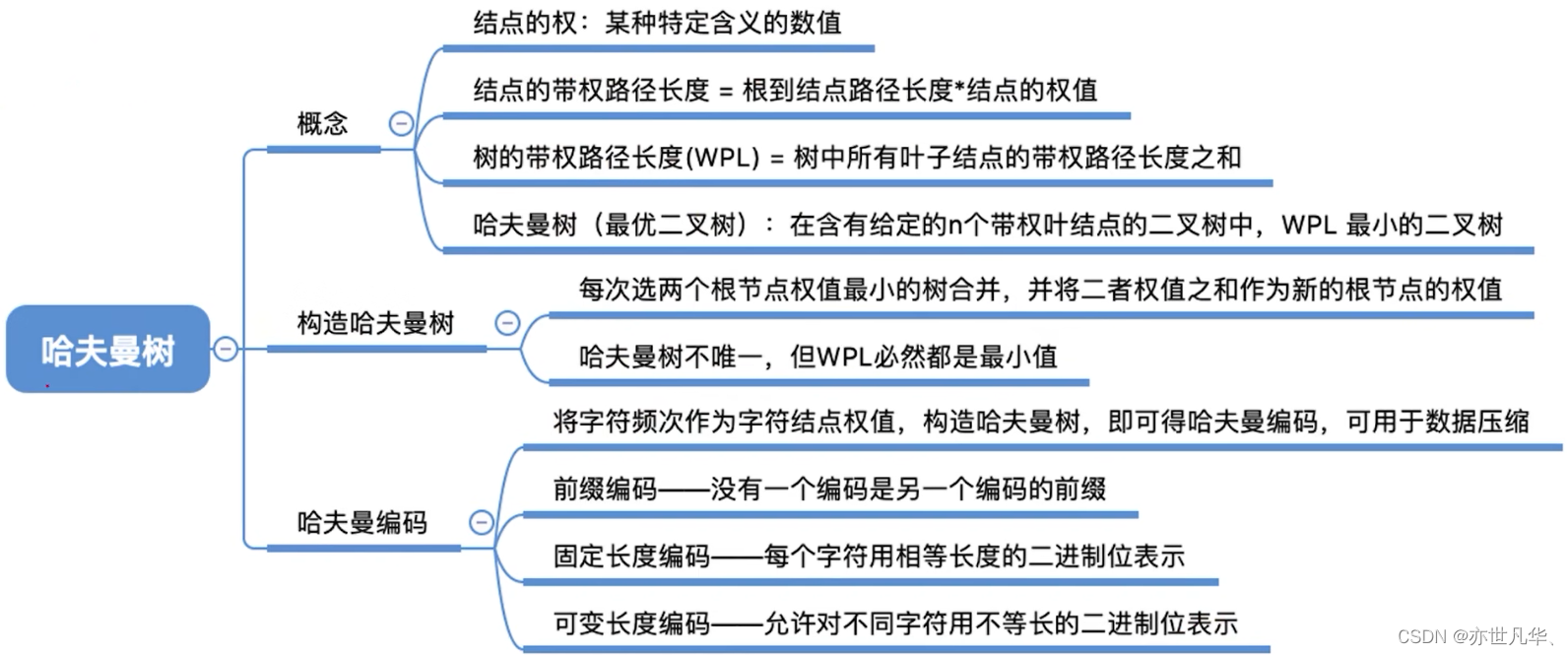
霍(哈)夫曼树
了解概念
结点的权:有某种现实含义的数值(如:表示结点的重要性等)
结点的带权路径长度:从树的根到该结点的路径长度(经过的边数)与该结点上权值的乘积:


举出以下的例子进行相应说明:
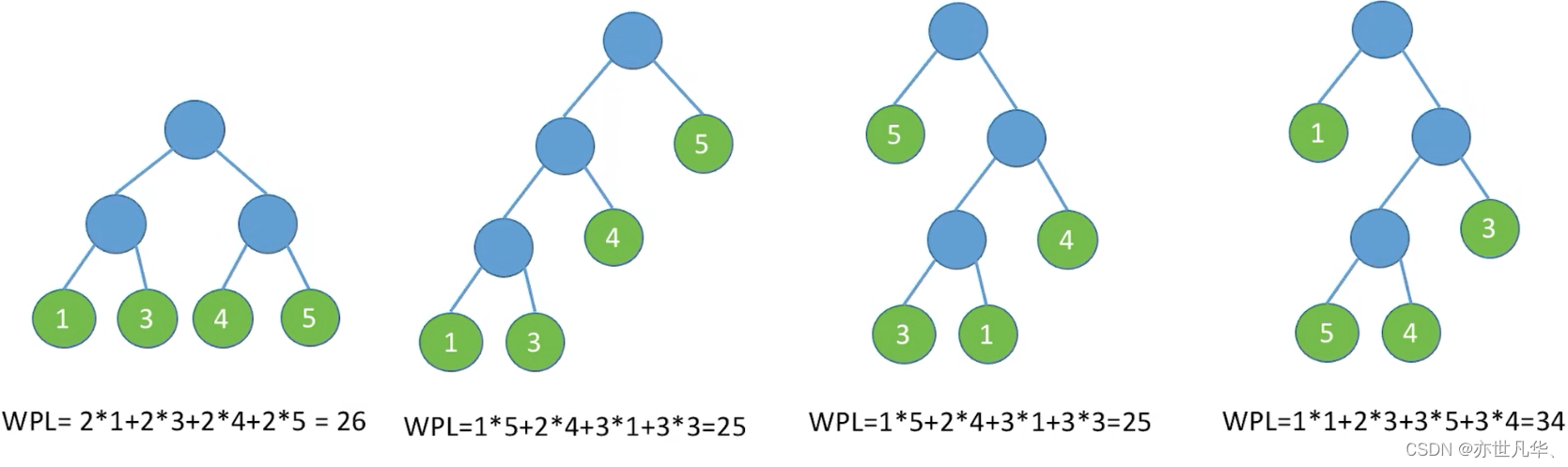
注意:在含有n个带权叶结点的二叉树中,其中带权路径长度(WPL)最小的二叉树称为哈夫曼树,也称最优二叉树。 因此我们可以根据这个特点对哈夫曼树进行构造:
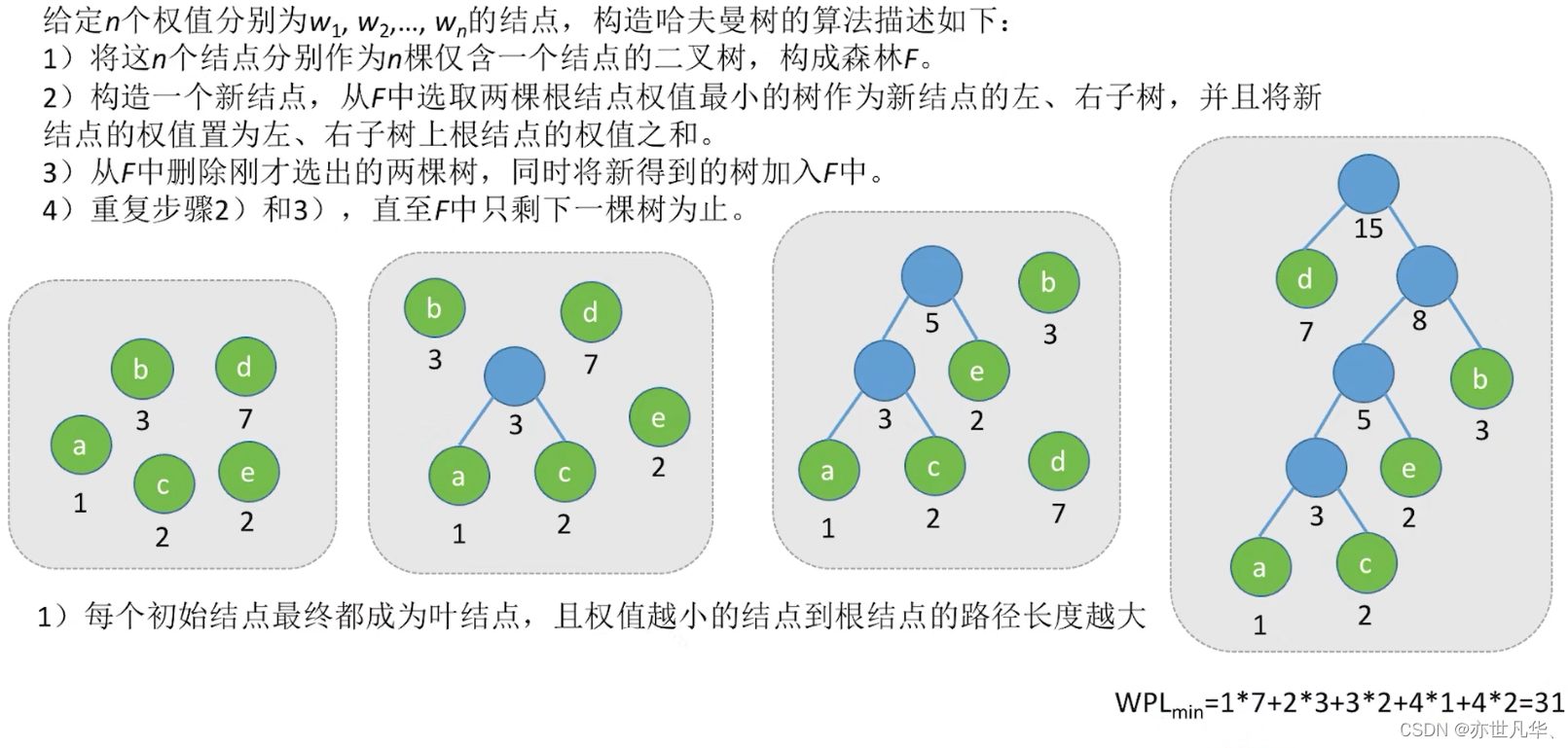
哈夫曼编码:
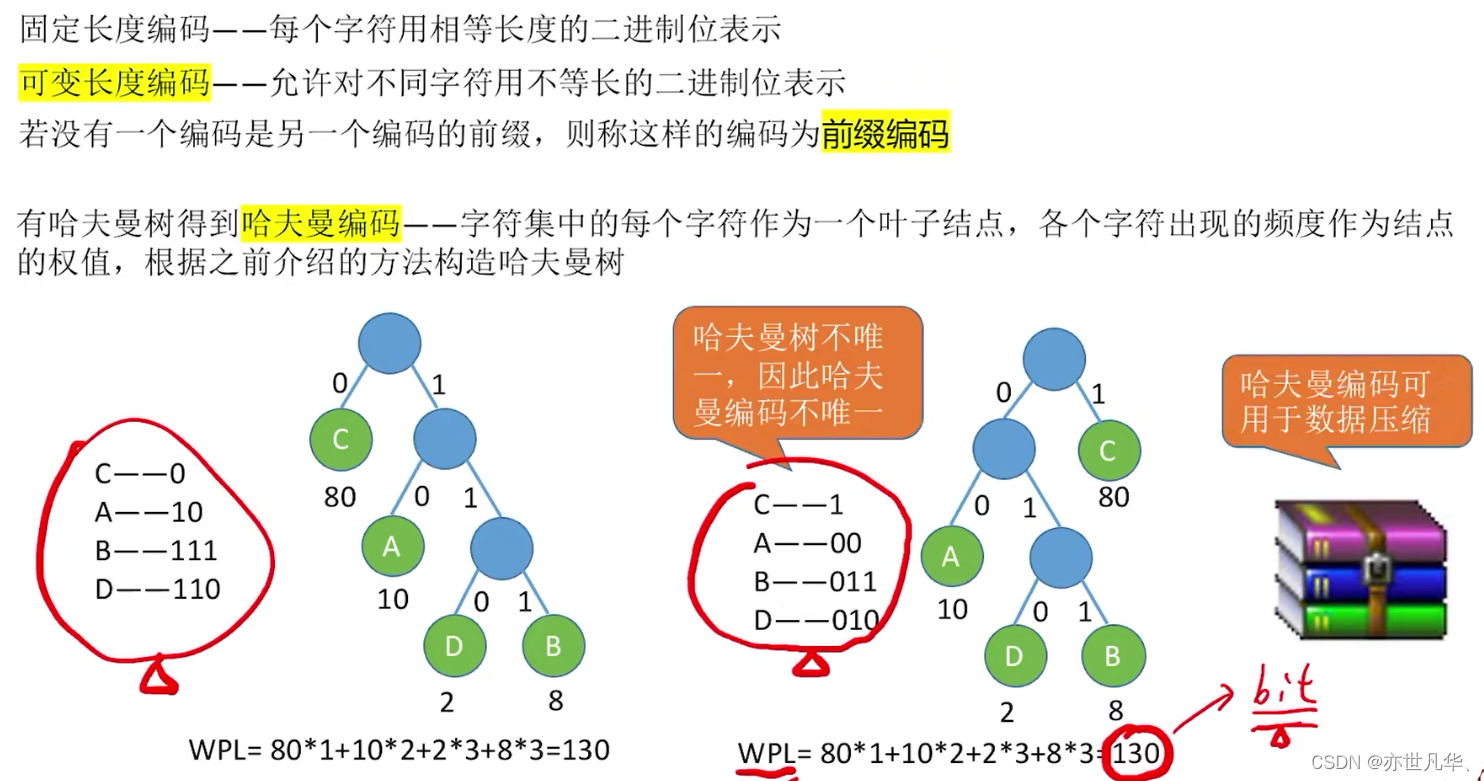
回顾重点,其主要内容整理成如下内容: