区块链技术-比特币数据结构

背景

随着近几年区块链技术的迅速发展，越来越多的行业正在将区块链技术应用到实际中去。例如，金融、物流、交易所等行业都开始尝试使用区块链技术来替代传统技术。伴随着区块链迅速发展的期间，诞生了比特币（BTC）、以太币（ETH）等新兴资产，吸引了来自世界各地的投资者。近期，在了解web3项目技术，同时学习区块链的相关技术，特地跟大家分享下比特币相关知识。

比特币概述

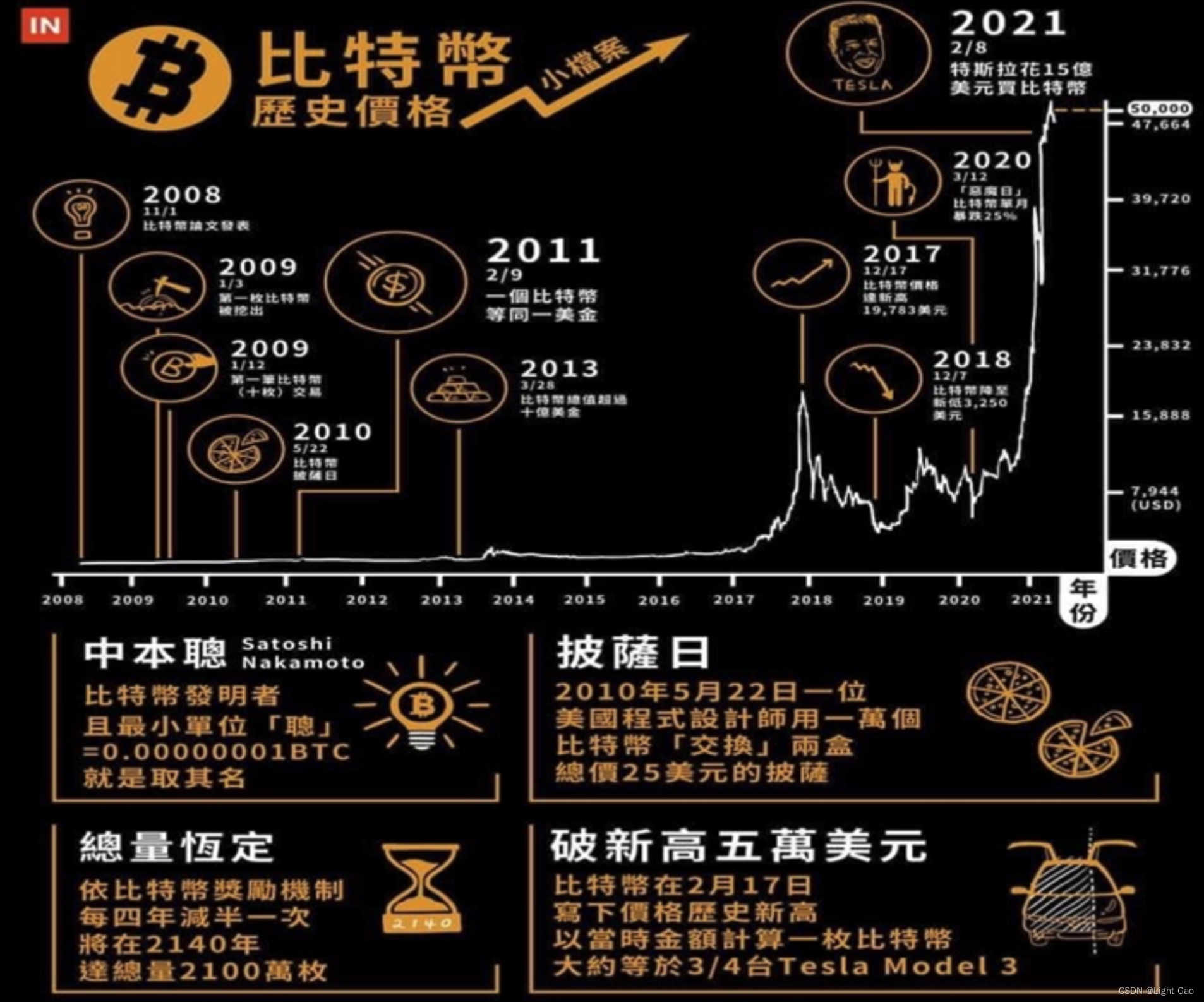
比特币是基于区块链技术的第一个去中心化应用，它可以追溯到2009年创立时。在过去几年，比特币已经成为全球金融市场上受关注的新兴资产，吸引了来自世界各地的投资者。比特币的发展背后是一种技术，即区块链技术。通过使用数字签名和分布式数据库技术，这种技术可以保证交易的安全性、不可篡改性和去中心化。
在这里插入图片描述

中心化与去中心化架构区别

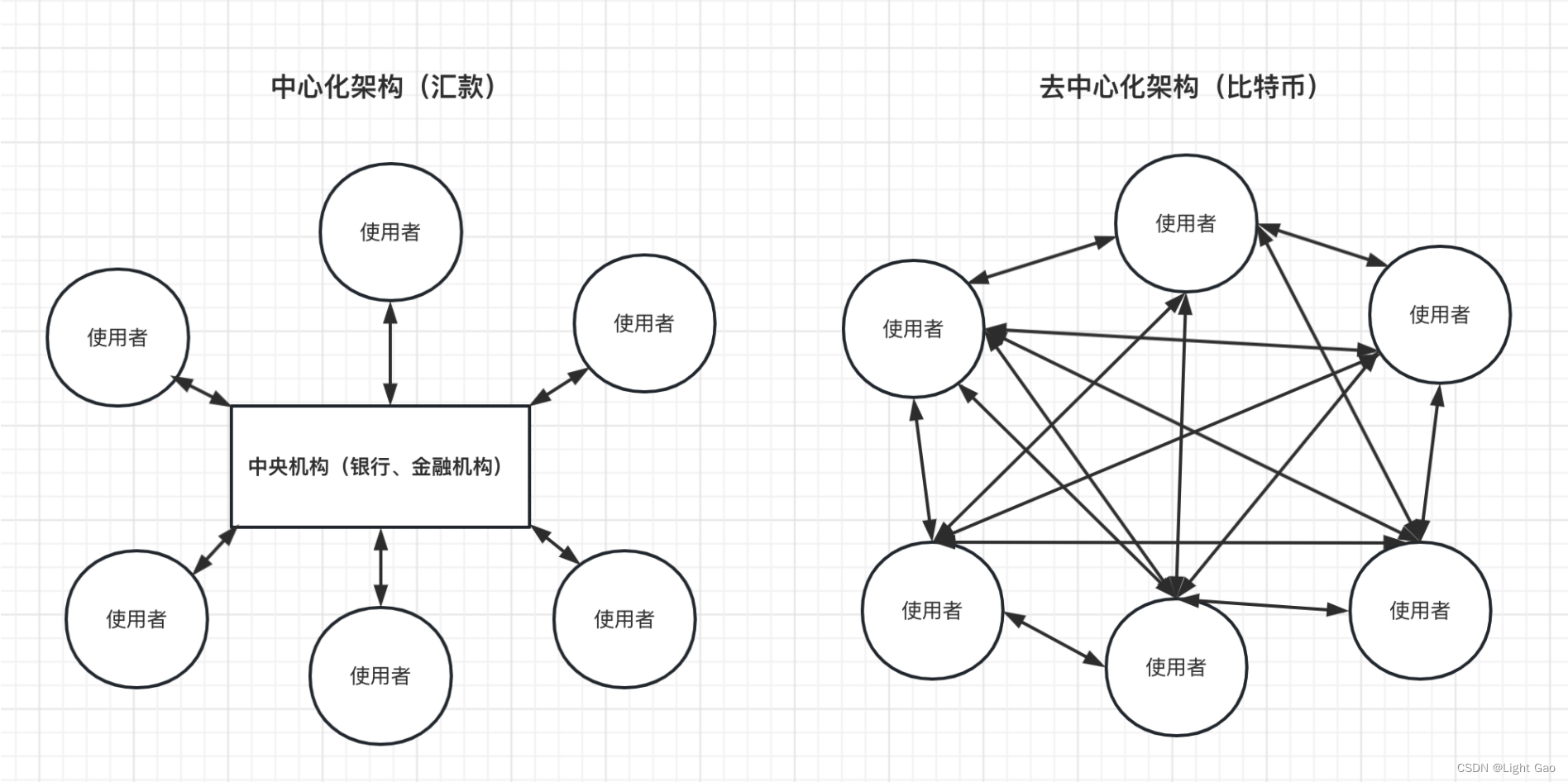
在这里插入图片描述
去中心化的货币架构，实现币的所有权掌握在个人手上，相比于法币，转账交易更加自由，并且交易过程不需要花费如此多的资源，不需要成立银行记账、转账、确认等一堆程序，只需要家中有一台电脑，就可以完事，转账时间正常情況几小时内搞定，如果肯多出一點手续费，那10分钟内便可完成。

比特币与密码学

比特币（BitCoin）虽然被称为加密货币（crypto-currency），但它本身是不加密的，区块链上内容都是对外公开，包括区块的地址，转账的金额等。它的”加密性“主要借助密码学中的”哈希“与”签名“两操作来实现的。

比特币主要用到了密码学中的两个功能: 哈希与签名

Hash算法：Cryptographic Hash Function

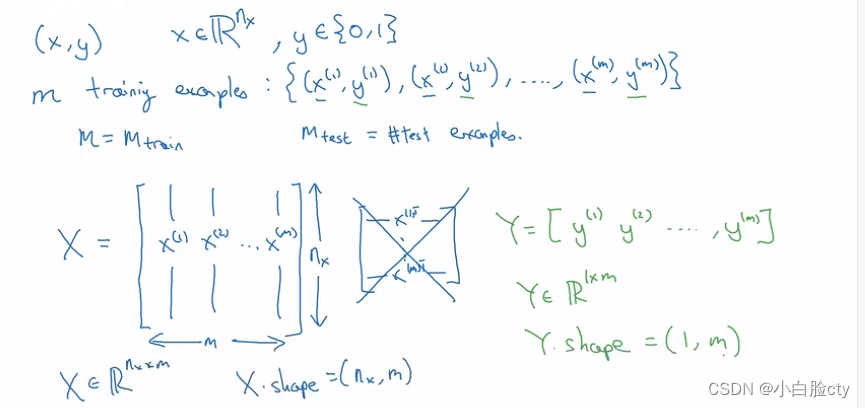
Collision Resistance（抗碰撞性，不可人为创造产生hash碰撞）: 例如 x≠y H(x)=H(y) 两个不同的输入，输出却是相等的，这就称哈希碰撞。它是不可避免的，因为输入空间总大于输出空间。比如：给出x，很难有高效的办法找到y，使得H(x)=H(y)，除非穷举求解(brute-force)。客观来说哈希碰撞无法找到人为制造的方法，但不是所有的函数都具有这个特性，例如MD5，可以人工找到哈希碰撞。
hiding（隐藏、不可逆）：哈希函数的计算过程是单向的，不可逆的。(从H(x)无法推导出x) hiding性质前提是输入空间足够大，分布比较均匀。如果不是足够大，一般在x后面拼接一个随机数，如H(x||nonce)。
比特币中用到的哈希函数还有第三个性质: puzzle friendly 指哈希值的预算事先是不可预测的。假如哈希值是00…0XX…X，一样事先无法知道哪个值更容易算出这个结果，还是要一个一个带入。

比特币中用的哈希函数叫作SHA-256(secure hash algorithm )以上三个性质它都是满足的。

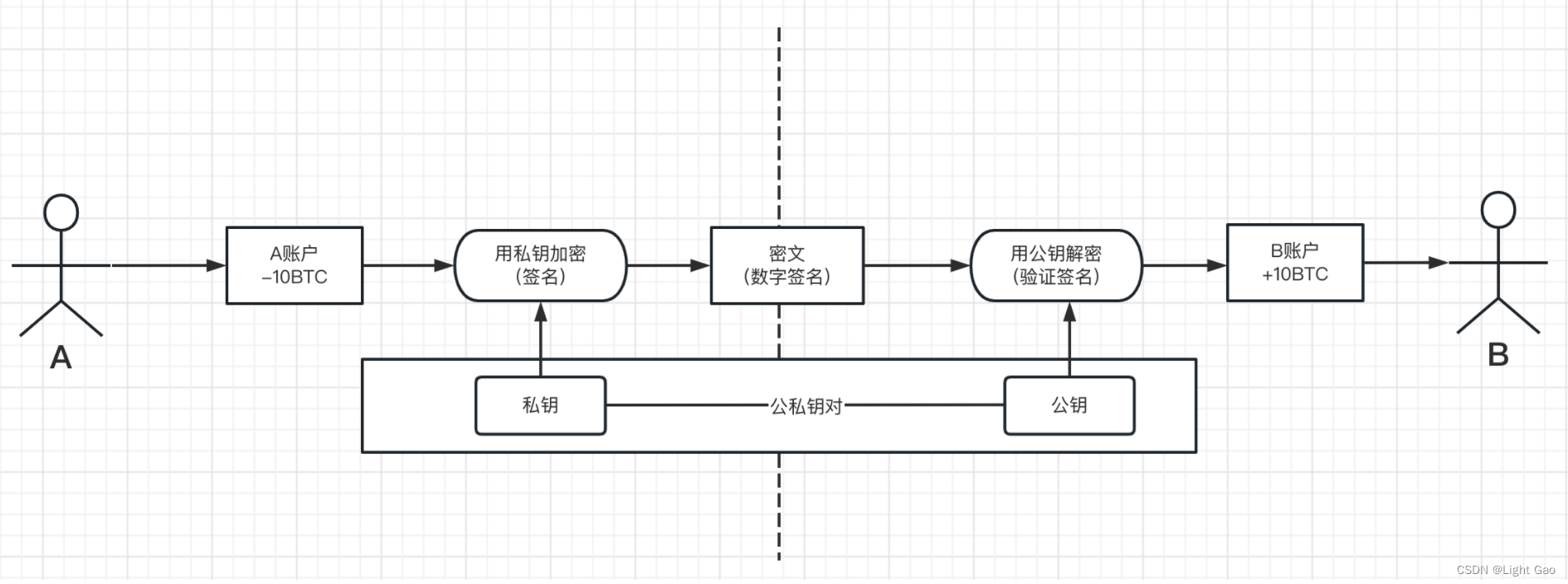
签名：比特币签名采用的是非对称的加密技术，即本地生成一个公私钥对(public key ,private key)，对外表示为一个账号。

假如A想向B转10个比特币，A把交易放在区块链上，别人怎么知道这笔交易是A发起的呢?这就需要A要用自己的私钥给交易签名，其他人收到这笔交易后，要用A的公钥去验证签名。签名用私钥，验证用公钥，用的仍然是同一个人的。创建账户产生相同公私钥的可能性微乎其微，所以大量创建账户来窃取其他人账户是不可行的。
在这里插入图片描述

比特币的数据结构

比特币系统中使用的数据结构主要是以下两种：

哈希指针（hash pointers）
merkle树（merkle tree）

哈希指针用于区块之间的连接作用，而merkle tree用于每个区块内部交易之间的连接作用。哈希指针与merkle tree的关系如下图所示：

哈希指针（Hash Pointers）

普通指针与Hash指针

普通指针存储的是某个结构体在内存中的地址。假如P是指向一结构体的指针，那么P里面存放的就是该结构体在内存中的起始位置。

哈希指针除了要存地址之外，还要保存该结构体的哈希值H(x) 。这样的好处是:从这个哈希指针，不仅可以找到该结构体的位置，同时还能够检测出该结构体的内容有没有被篡改，因为我们保存了它的哈希值。

区块链和普通的链表

比特币中最基本的结构就是区块链，区块链就是一个一个区块组成的链表。区块链和普通的链表相比有什么区别:

用哈希指针代替了普通指针(B block chain is a linked list using hash pointers)
区块链第一个区块叫作创世纪块(genesis block) ，最后一个区块叫做最近产生的区块(most recent block)，每一个区块都包含指向前一个区块的哈希指针。
普通链表可以改变任意一个元素，对链表中其他元素是没有影响的。而区块链是牵一发而动全身，如果区块链中任一块被修改，则后面所有的区块都要发生变动（因为后一个区块头部存储是前面所有区块求H()后的值），所以只需要保存最后一个哈希值，就可以判断区块链有没有改变。针对这一特性，比特币没有要保存所有区块的内容，可以只保留最近的几千个区块。如果要用到以前的区块，可以向系统中其他节点要这个区块。假设整个区块链当中有些节点是有恶意的，它给出块算出它的哈希值，与保留的区块的哈希值对比即可判断是否为异常节点。

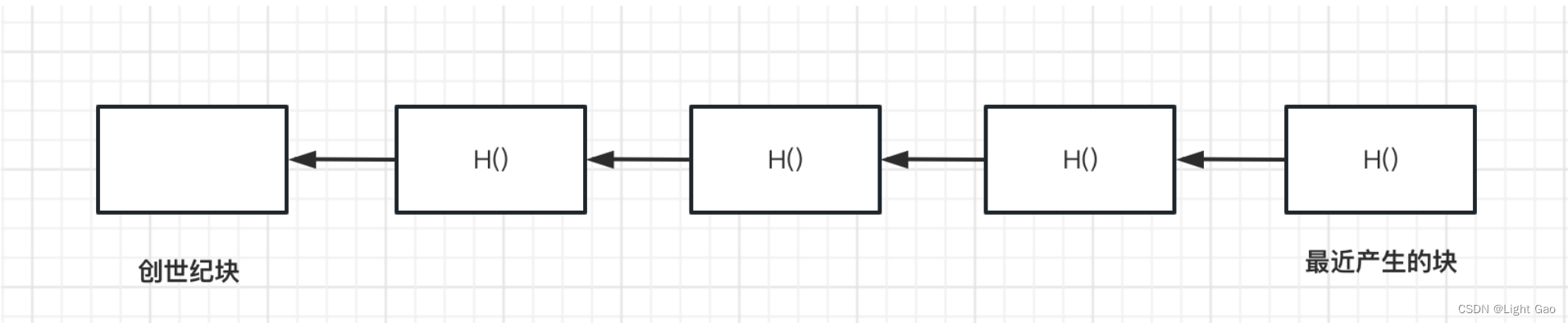
由上图可看到，区块链系统中的的每个节点可以获得最近一个区块的哈希值H(recent block)，从而就可以追溯到创世纪块。

通过哈希指针的链式结构，也可以知道区块内容是否被篡改，因为只要某个区块A被篡改，它的哈希值就会改变，它之后区块B的哈希指针就不会指向A了，这样系统会很快知道A被篡改。或者篡改者从区块A一直改到最新区块，到最后最新区块的哈希值也会改变，跟系统中保存的最近区块哈希值H(recent block)对比，也就很快发现是否被篡改。

Merkle Tree（树形结构）

Merkle tree跟二叉树很类似，只不过把普通指针同样换成了哈希指针。

Merkle tree在每个区块内部将各个交易连接起来了，如下图所示：
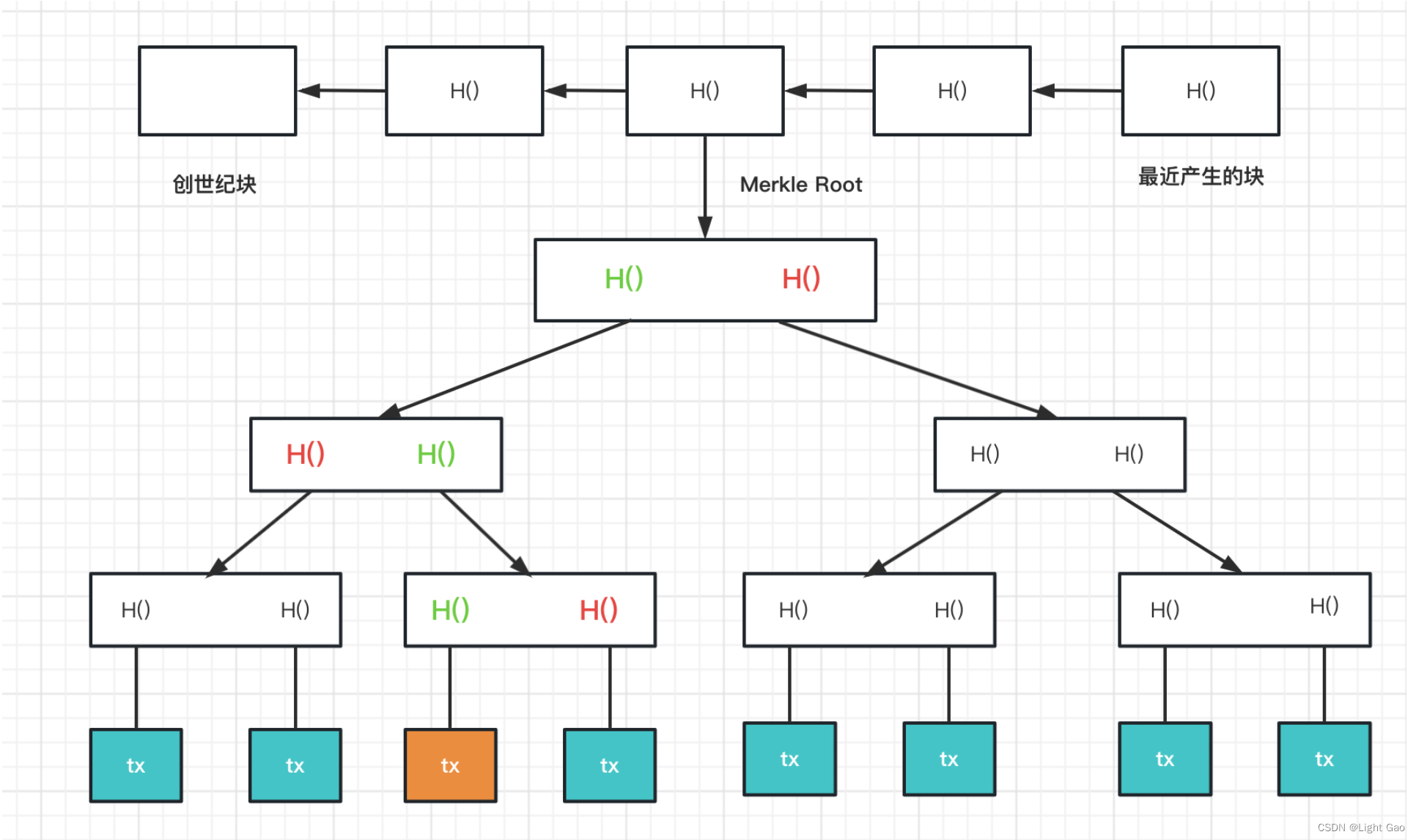
在这里插入图片描述
这个树的最下面是的叶子节点是区块体（block body）里的所有交易，每个交易取哈希值，相邻交易的哈希值结合起来一起取哈希，层层往上取哈希，直到得到最后一个哈希值，这个哈希值也就是根哈希值（root hash），并存在区块头（block header）。

从上面分析得到，只要记住了根哈希值（root hash），就可以检测出对树的任何节点的修改。要想改变其他节点的哈希值同时保证根哈希值的不变，就必须人为制造哈希碰撞，但通过哈希的性质知道，这是不可能的。

Merkle tree 的作用：提供Merkle proof

Merkle proof是Merkle tree内的从最底层的某个交易出发到最顶部根哈希的一条路径。如上图中最下面的黄色交易开始到最底部的路径就是一个merkle proof。

在比特币区块链网络中有很多节点，包括计算机、手机、矿机、服务器等等。在所有节点中分为：全节点和轻节点。

全节点（full node）：保存了区块的所有内容，区块头和区块体。

轻节点（light node）：只保存了区块头，比如手机中的比特币钱包。

问题：如何向一个轻节点证明某个交易是写入区块链的?

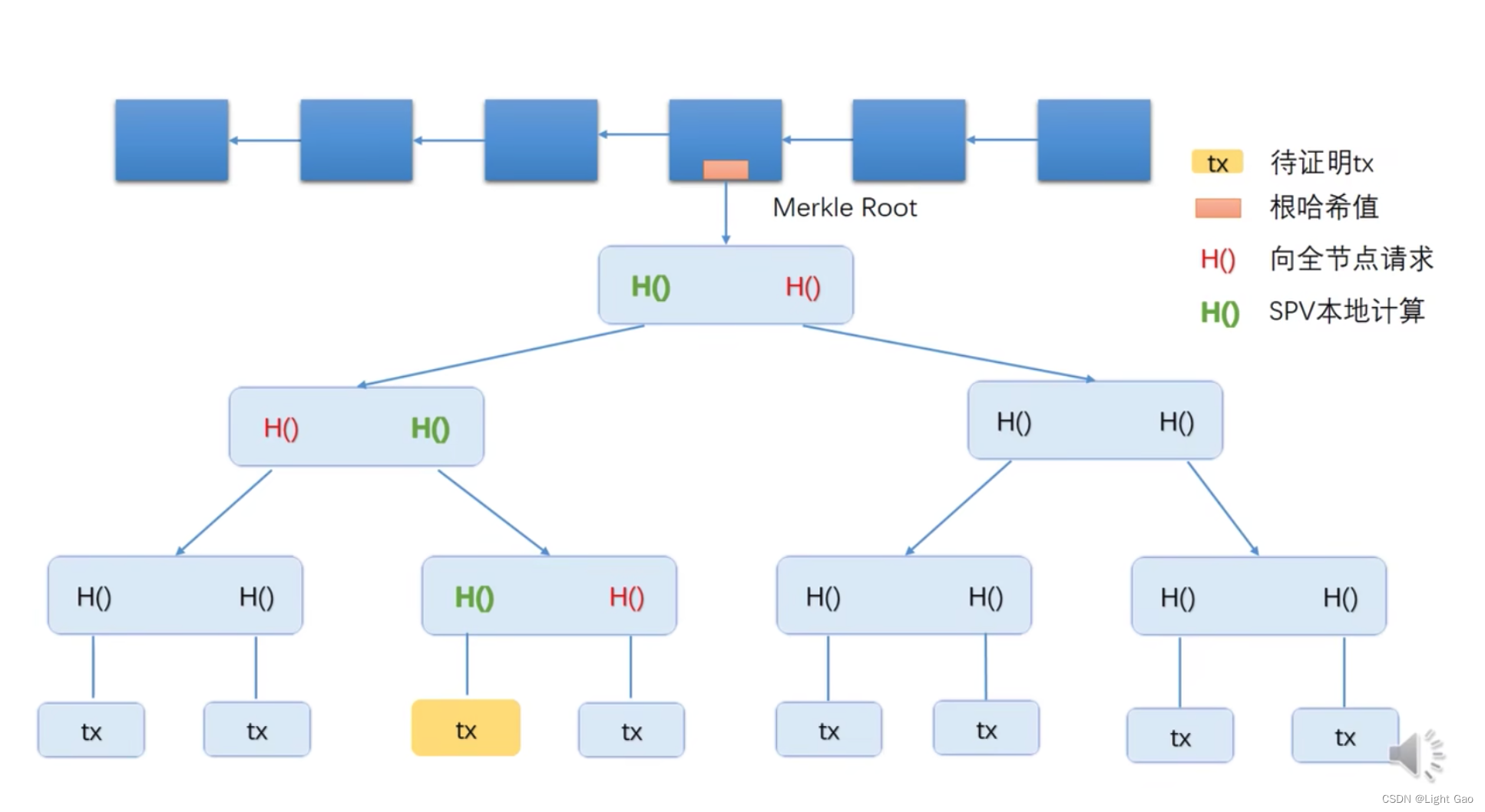
在这里插入图片描述
假设某个轻节点想知道图中黄色的交易，是否包含在了merkle tree里面。该轻节点没有包含交易列表，没有这颗merkle tree的具体内容，只有一个根哈希值。这时轻节点向一个全节点发出请求，请求证明黄色的交易被包含在这颗merkle tree里面的merkle proof（由交易者提供）。全节点收到这个请求之后，只需要将图中标为红色的这三个哈希值发给轻节点即可。

有了这些哈希值之后，轻节点可以在本地计算出图中标为绿色三个哈希值。

首先算出黄色交易的哈希值，即它正上方的那个绿的哈希值，然后跟旁边红色的哈希值拼接起来，可以算出上层节点绿色的哈希值。
然后再拼接，再算出上层绿色哈希值，再拼接，就可以算出整棵树的根哈希值。
轻节点把这个根哈希值和block header里的根哈希值比较一下，就能知道黄色的交易是否在这颗merkle tree里。
全节点在merkle proof里提供的这几个哈希值，就是从黄色的交易所在的节点的位置到树根的路径上用到的这些哈希值。轻节点收到这样一个merkle proof之后，只要从下往上验证，沿途的哈希值都是正确的即可。(验证时只能验证该路径的哈希值，其他路径是验证不了的，即该图中红色的哈希值是验证不了的)

这样是否不安全呢? 假如黄色交易被篡改，它的哈希值发生了变化，那能不能调整旁边红色的哈希值，使得它们拼接起来的哈希值是不变的呢? 不行，根据collision resistance，这是不可行的。

问题：如何证明merkle tree里面没有包含某个交易?

1.全节点将整个区块所有交易信息发给轻节点，这样可以证明某个交易不在区块中，但这是非常不高效的方法且比较笨的方法。

2.思路还是根据merkle proof计算根哈希值，轻节点向全节点对这个交易发出请求，全节点为了证明此交易不在区块链中。

全节点只需以下这样做即可：

对区块中所有交易的哈希值进行排序，然后计算要证明的交易的哈希值，根据二分查找法来确定这个交易哈希值的位置，再将此位置相邻的2个交易merkle proof发送给轻节点。

轻节点只需以下这样做即可：

轻节点收到merkle proof后，根据merkle proof计算得到最后的根哈希值（root hash），若计算得到的根哈希值跟本地的区块头中的根哈希值比较一样，则证明此交易一定不在区块链中，因为如果在的话，最后计算出来的根哈希值比较必然是不一样的。

可以把整棵树传给轻节点，轻节点收到后验证树的构造都是对的，每一层用到的哈希值都是正确的，说明树里只有这些叶节点，要找的交易不在里面，就证明了proof of non-membership。问题在于，它的复杂度是线性的θ(n)，是比较笨的方法。

如果对叶节点的排列顺序做一些要求，比如按照交易的哈希值排序。每一个叶节点都是一次交易，对交易的内容取一次哈希，按照哈希值从小到大排列。要查的交易先算出一个哈希值，看看如果它在里面该是哪个位置。比如说在第三个第四个之间，这时提供的proof是第三个第四个叶节点都要往上到根节点。如果其中哈希值都是正确的，最后根节点算出的哈希值也是没有被改过的，说明第三、四个节点在原来的merkle tree里面，确实是相邻的点。要找的交易如果存在的话，应该在这两个节点中间。但是它没有出现，所以就不存在。其复杂度也是log形式，代价是要排序。排好序的叫作sorted merkle tree。比特币中没有用到这种排好序的merkle tree，因为比特币中不需要做不存在证明。