🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨
🐻强烈推荐优质专栏: 🍔🍟🌯C++的世界(持续更新中)
🐻推荐专栏1: 🍔🍟🌯C语言初阶
🐻推荐专栏2: 🍔🍟🌯C语言进阶
🔑个人信条: 🌵知行合一
🍉本篇简介:>:记录力扣题 二叉树的层序遍历

一、二叉树的层序遍历

题目名称: 二叉树的层序遍历
题目链接:传送门
题目难度:中等

题目描述:

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

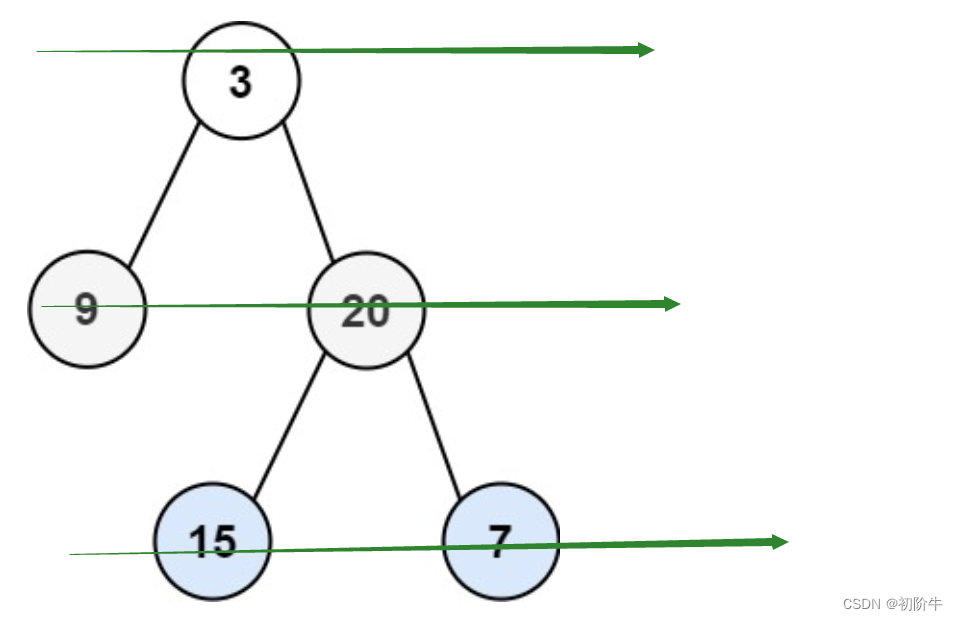
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

解题思路:

1. 创建一个队列,需要借助队列的性质去访问结点. queue<TreeNode*> q1;
2. 创建一个二维数组,存储层序遍历的结果.vector<vector<int>> vv1;
3. 创建一个一维数组,存储每层的数据. vector<int> v1;
4. 将根节点入队列.

难点:出队列时,如何确定什么时候是一层的结束?
答案: 出队列前,队列的长度,也就是元素个数.

示例:

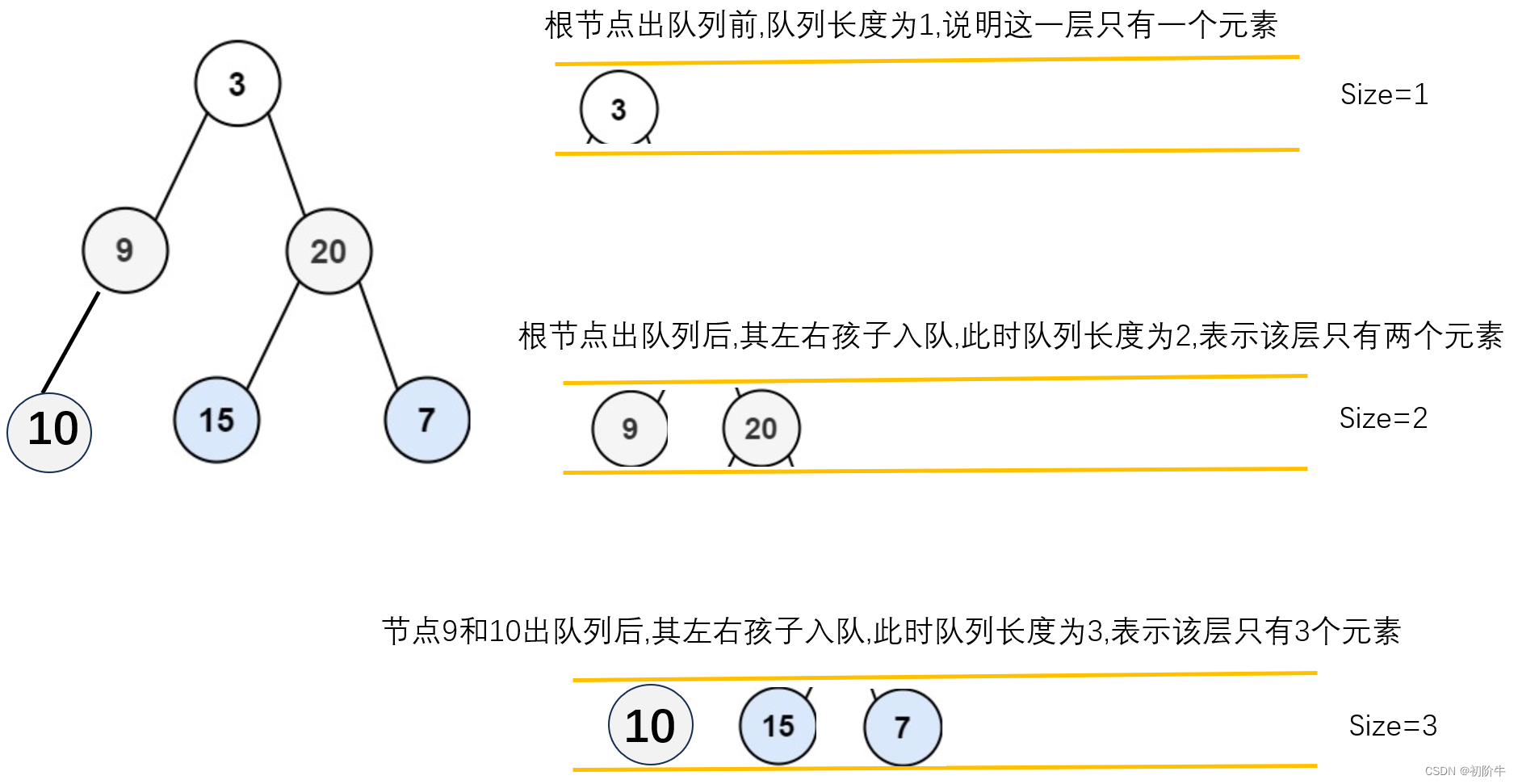
5. 我们定义一个count变量,用于记录出队列前,队列的长度.
6. 以count为条件,进行出队列,将这一层的数据插入进 vector<int> v1;
7. 一层数据获取完毕后,将这一层数据存入二维数组vv1;
8. 返回这个二维数组即可.

代码实现:

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> q1;        //定义一个存树结点的队列
        vector<vector<int>> vv1;  //定义一个二维数组
        
        if(root==nullptr)   //空树直接返回
        {
            return vv1;
        }
        q1.push(root);  //根节点入队列

        while(!q1.empty())
        {
            int count=q1.size();    //每一层的数量
            vector<int> v1;     //用于存放每一层的结点数据
            for(int i=0;i<count;i++)
            {
                TreeNode* node=q1.front();
                v1.push_back(node->val);
                q1.pop();
                
                //孩子入栈
                if(node->left)q1.push(node->left);
                if(node->right)q1.push(node->right);
            }
            vv1.push_back(v1);      //将这一层的数据插入
        }
        return vv1;
    }
};

二、二叉树的层序遍历 II

题目描述

题目名称: 二叉树的层序遍历 II
题目链接:传送门
题目难度:中等

给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

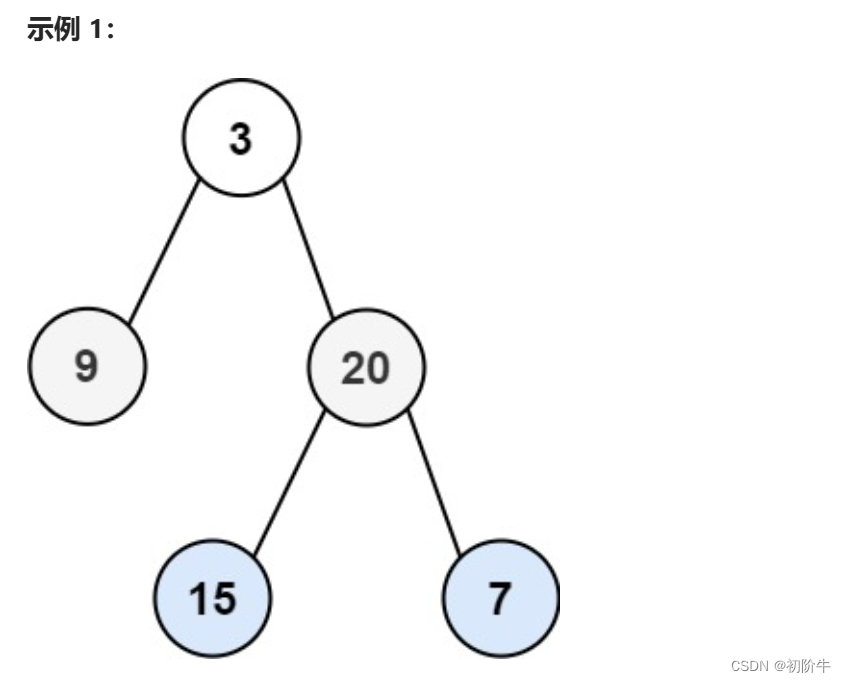
示例1:

输入：root = [3,9,20,null,null,15,7]
输出：[[15,7],[9,20],[3]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

解题思路:

如何从下往上打印呢?还是先从根节点开始入队列吗?
当你还在犹豫、考虑如何下手的时候,牛牛已经在开心的做一名cv工程师了!

只需要在上一题的基础上,将二维数组逆置一下,每一行即可.

只需一行代码,解决问题,美滋滋!

reverse(vv1.begin(),vv1.end());

代码实现:

class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        queue<TreeNode*> q1;        //定义一个存树结点的队列
        vector<vector<int>> vv1;  //定义一个二维数组
        
        if(root==nullptr)   //空树直接返回
        {
            return vv1;
        }
        q1.push(root);  //根节点入队列

        while(!q1.empty())
        {
            int count=q1.size();    //每一层的数量
            vector<int> v1;     //用于存放每一层的结点数据
            for(int i=0;i<count;i++)
            {
                TreeNode* node=q1.front();
                v1.push_back(node->val);
                q1.pop();
                
                //孩子入栈
                if(node->left)q1.push(node->left);
                if(node->right)q1.push(node->right);
            }
            vv1.push_back(v1);      //将这一层的数据插入
        }
        reverse(vv1.begin(),vv1.end());		//只需一步
        return vv1;
    }
};