算法-动态规划/中心扩散法-最长回文子串
1 题目概述
1.1 题目出处
https://leetcode.cn/problems/longest-palindromic-substring
1.2 题目描述

2 动态规划
2.1 思路
dp[i][j] 表示[i,j]之间的字符串是否是回文。
那么,如果chars[i] = chars[j]时,就有可能构成的子串为回文:
- 如果j - i < 3,则子串肯定是回文。比如 aba、aa、a
- 如果j - i >=3,则就会用到动态规划了,即 dp[i][j] = dp[i+1][j-1],也就是说 i的下一个字符和j的前一个字符组成的闭区间子串是否是回文,只要是那么本子序列也是。
- 这里有个重要的点,表达式为dp[i][j] = dp[i+1][j-1],也就是说i取决于i+1,j取决于j-1,所以遍历时需要i从大到小计算,而j需要从小到大计算。
- 遍历过程中,每当判断子序列为回文,就和之前已经找到的最大回文长度的比较,如果更长就更新,并记录下i、j
- 最后将字符串从i、j取子序列即可
2.2 代码
public class Solution {
public String longestPalindrome(String s) {
// 表示[i,j]之间的字符串是否是回文
boolean[][] dp = new boolean[s.length()][s.length()];
for(int i = 0; i < s.length(); i++) {
// 定义同一个位置的为true
dp[i][i] = true;
}
int maxLength = 0;
int left = 0, right = 0;
for (int i = s.length() - 1; i >= 0; i--) {
for (int j = i + 1; j < s.length(); j++) {
if (s.charAt(i) == s.charAt(j)) {
if (j - i < 3) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i+1][j-1];
}
if (dp[i][j] && (j - i + 1 > maxLength)) {
maxLength = j - i + 1;
left = i;
right = j;
}
}
}
}
return s.substring(left, right+1);
}
}
2.3 时间复杂度
O(N^2)
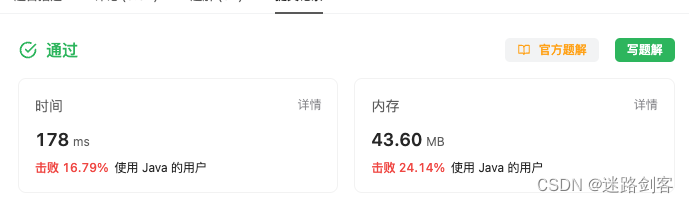
2.4 空间复杂度
O(N^2)
3 中心扩散
3.1 思路
从左到右移动,每当移动一次后,往两边扩散,直到两侧边界字符不符合回文规则。
3.2 代码
public class Solution {
int maxLength = 0;
int left = 0, right = 0;
public String longestPalindrome(String s) {
for (int i = 0; i < s.length() - 1; i++) {
// 字符串奇数长度时,中间一个字符串往两边扩散
spread(i, i, s);
// 字符串偶数长度时,中间两个字符串往两边扩散
spread(i, i+1, s);
}
return s.substring(left, right+1);
}
private void spread(int i, int j, String s) {
while (i >= 0 && j < s.length()) {
if (s.charAt(i) != s.charAt(j)) {
break;
}
i--;
j++;
}
// 把多减了、加了的补上
i++;
j--;
if (j - i + 1 > maxLength) {
left = i;
right = j;
maxLength = j - i + 1;
}
}
}
3.3 时间复杂度
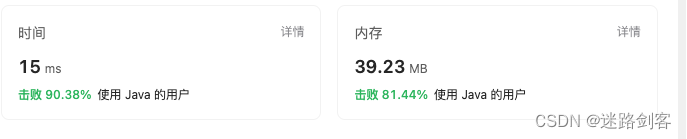
O(N^2)
3.4 空间复杂度
O(1)
参考文档
- 动态规划、中心扩散
- 图解马拉车算法