题目大意

让你求最多有多少个不相交的最长上升子序列。

思路

我们可以将数 $a_i$ 看成一个点 $(i,a[i])$，于是我们可以按照 $x$ 递增 $y$ 递减考虑分层。

分层的方法就是从 $1$ 到当前点的 LIS 即为其所在层数。

此时 LIS 的长度就是层数，再考虑对于序列的可能性。

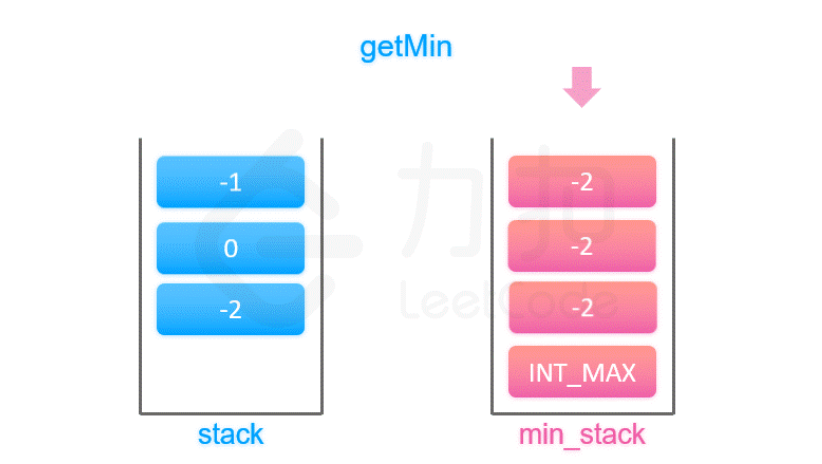
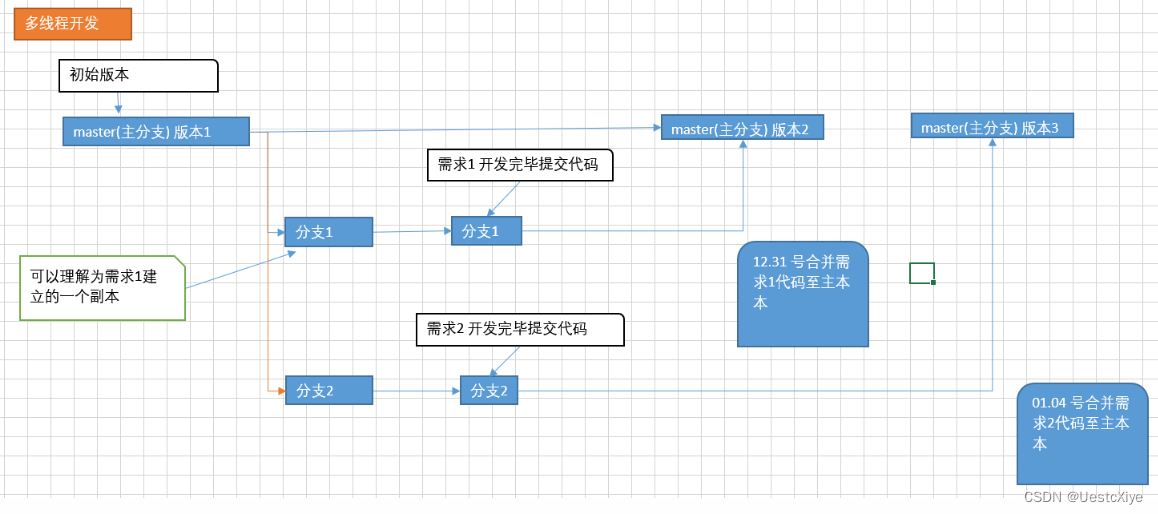
此时不能简单的想为每一层的数的个数的最小值，如下图就是一个反例。

我们直接贪心每一个序列能否填当前数即可，如果贪心不出来，即在下一层找不到满足条件的点，就直接弹出即可。

具体判断可以看代码实现。

时间复杂度是 $O(n\cdot \log n)$。

代码

#include <bits/stdc++.h>
using namespace std;
int n, m, b[1000005], s[1000005], a[1000005], nxt[1000005];
vector<int> ans[1000005];
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {//分层
        scanf("%d", &a[i]);
        int l = 1, r = m, mid;
        while (l <= r) {
            mid = l + r >> 1;
            if (a[b[mid]] > a[i])
                r = mid - 1;
            else
                l = mid + 1;
        }
        if (r == m)
            m++, b[m] = i, s[m]++;
        else
            nxt[i] = b[r + 1], b[r + 1] = i, s[r + 1]++;
    }
    int minn = 0, ansm = 0;
    for (int i = 1; i <= m; i++) minn |= (s[i] == 0);
    while (minn == 0) {//判断每一个数列是否可行
        ansm++;
        for (int j = 1; j <= m; j++) {
            while (!ans[ansm].empty() && b[j] != 0 && a[b[j]] < a[ans[ansm].back()])
                b[j] = nxt[b[j]], s[j]--, minn |= (s[j] == 0);
            if (b[j] == 0) {
                minn = 1;
                ansm--;
                break;
            }
            if (!ans[ansm].empty() && b[j] < ans[ansm].back()) {//此时上一个数在这一层找不到任何x，y都比它大的数
                j -= 2, ans[ansm].pop_back();
                continue;
            }
            ans[ansm].push_back(b[j]), b[j] = nxt[b[j]], s[j]--, minn |= (s[j] == 0);
        }
    }
    printf("%d %d\n", ansm, m);
    for (int i = 1; i <= ansm; i++, printf("\n"))
        for (auto g : ans[i]) printf("%d ", g);
    return 0;
}