量化交易全流程（七）

本节目录

资金分配

实盘交易

vn.py框架

我将重点介绍资金分配的基础模型和实现。当然，这里介绍的模型是最基础的模型，现实实践中往往并不能直接使用。因为后续我将加入机器学习和深度学习在量化交易领域中的应用。

现代 / 均值——方差资产组合理论

现代资产组合理论（Modern Portfolio Theory,MPT）是金融理论的重要基础。这一理论是由马克威茨（Harry Markowitz）首先提出的，因为这一理论，马克威茨荣获了1990年的诺贝尔经济学奖。
尽管这种方法早在20世纪50年代就已提出，但时至今日仍然是应用广泛。大量的投资组合理论都衍生于这个基本原理。均值﹣方差理论的核心思想是同时考察资产组合的预期收益和风险。研究当我们有一系列可选资产的时候，应如何对其配置资金权重，从而可以得到最好的收益风险比？本节将简单介绍均值﹣方差的基本理论以及Python的具体实现。

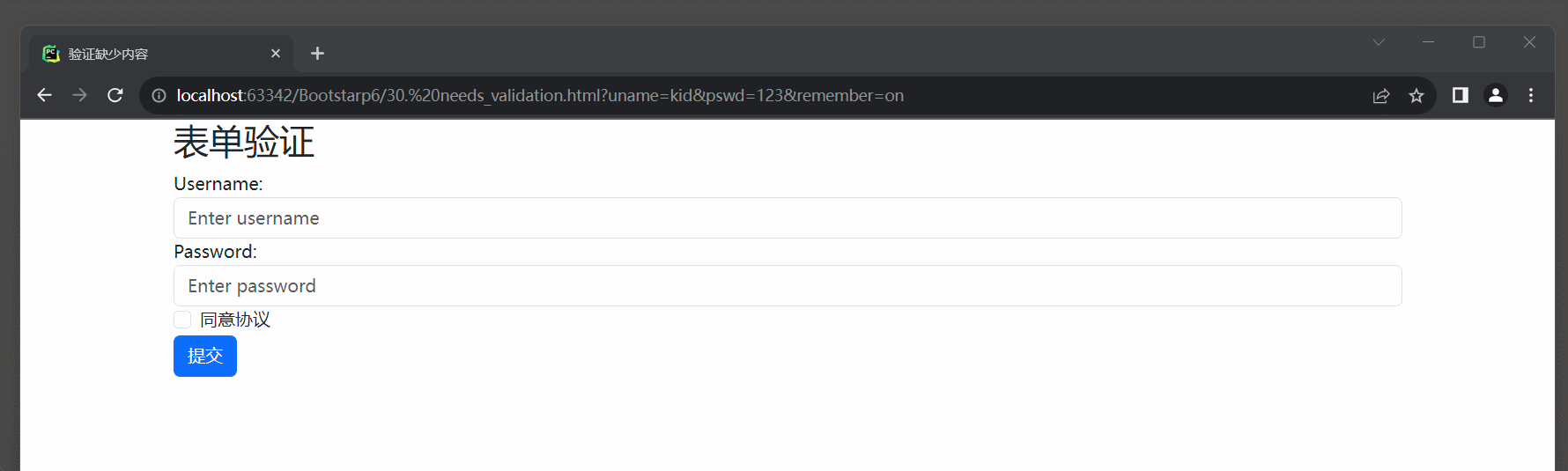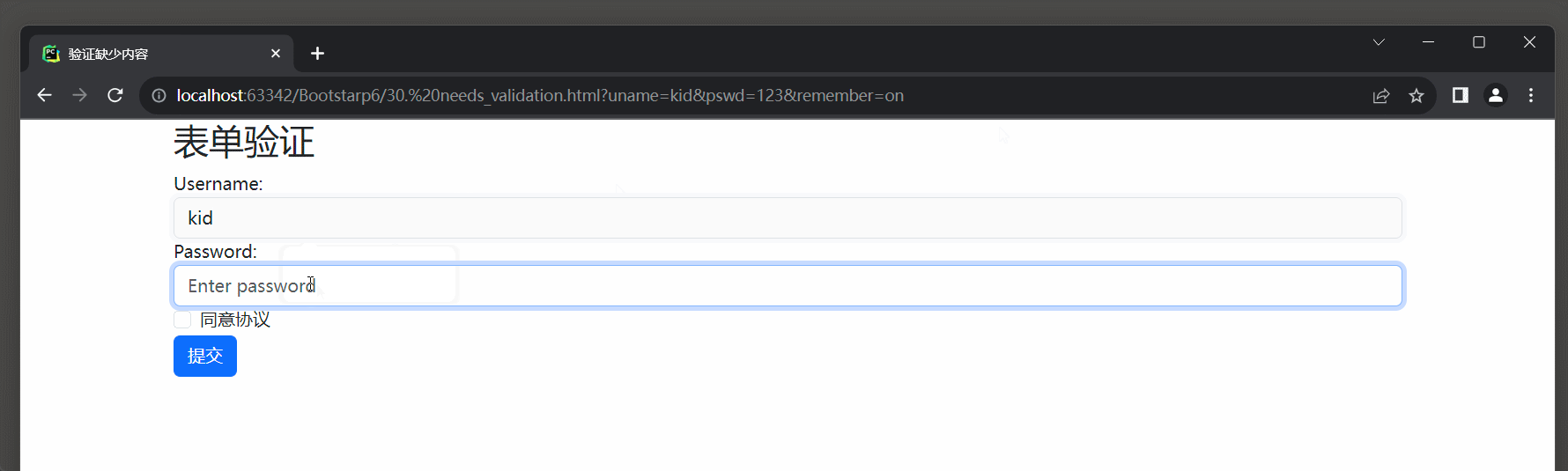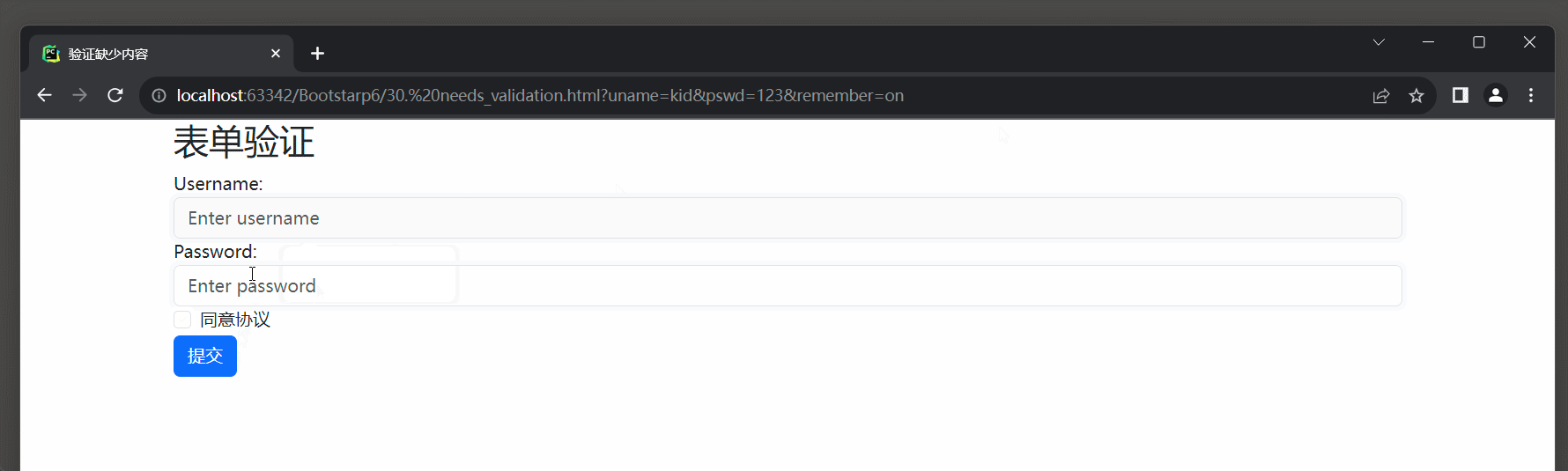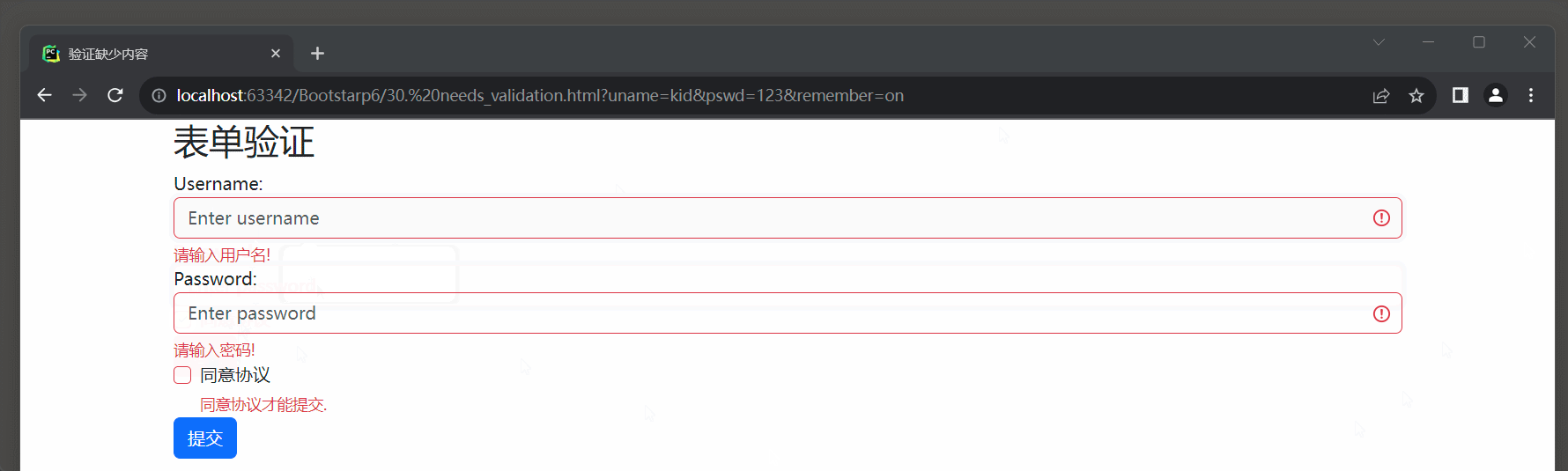
MPT理论简介：要实现MPT理论，我们需要做如下几个基本假设。
□ 假设资产的收益率符合正态分布。
□假设资产的预期收益率可以用历史收益率进行估计。
□假设资产的风险可以用资产收益率的方差（标准差）进行估计。
假设有n种资产，资产i的资金分配权重为w，所有资金的权重和为1，也就是： $\sum_{i}^{n}w_i=1$

假设资产i收益率为 $r_i$ ，那么组合收益率为：

$\mu_p=E(\sum_{N}^{}w_ir_i)=\sum_{I}^{}w_i\mu_i=w^T\mu$

为了得到组合的预期风险（方差），我们需要先计算协方差矩阵，由各个资产之间协方差组成。

利用投资组合协方差矩阵，我们可以得到投资组合的方差公式：

$\delta ^2_p=E(r-\mu)^2=w^T\sum w$

为了简单起见，我们假定无风险利率，即 $r_f$ =0。现在我们可以得到整个组合的夏普比率：

$SR=\frac{(\mu_p-r_f)}{\delta_p}=\frac{(\mu_p)}{\delta_p}$

现在我们的目标就是优化权重 w，获得尽可能大的夏普比率，即SR最大。

随机权重的夏普比率

在实际交易中，我们分配资金的对象往往是策略，而不是单纯地持有某种资产。先导入常见的模块，随机选择5只股票的收盘价进行计算得到日收益率，代码如下：

import mysql.connector
import pymysql
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

stock_codes = ['000001','000002','000004','000005','000006']
start_date = '20220904'
end_date = '20230904'
dt=pd.DataFrame()
conn=pymysql.connect(host = '127.0.0.1' # 连接名称，默认127.0.0.1
,user = 'root' # 用户名
,password='152617' # 密码
,port= 3306 # 端口，默认为3306
,db='stock_info' # 数据库名称
,charset='utf8' # 字符编码
)
cur = conn.cursor() # 生成游标对象
for stock_code1 in stock_codes:
        sql= "select * from `stocks` where stock_code = " + stock_code1 + " and date > " + start_date + " and date < " + end_date  # SQL语句
        cur.execute(sql) # 执行SQL语句
        data = cur.fetchall() # 通过fetchall方法获得数据
        df = pd.DataFrame(data)
        dt = pd.concat([dt,df],axis=0)
# print(df.head())
cur.close() # 关闭游标
conn.close() # 关闭连接
dt

对数据处理：

dt.columns= ['date','code','open','high','low', 'close','volumes'] # 修改列名
dt = dt[['date','code','close']]
print(dt)
d=dt
# 分组计算收益率
code_grouped = d.groupby('code')
returns = code_grouped['close'].pct_change()

# 合并到原始数据中
d['returns'] = returns
d = d.dropna()
print(d)
df_new = d.pivot(index='date', columns='code', values='returns')
df_new.columns=['s1','s2','s4','s5','s6']
print(df_new)
df_new = df_new.astype(float)
df_new.plot()
# 计算年化收益率，假设一年252交易日
df_new.mean() * 252

得到的结果如图：

计算协方差矩阵：

df_new.cov() * 252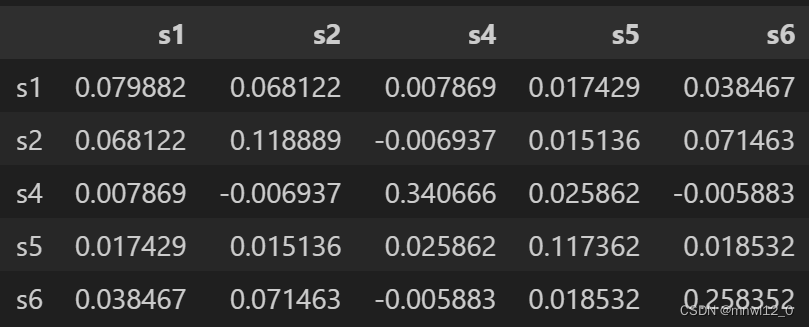

下面随机生成一组资金权重：

n=len(df_new.columns)
w=np.random.random(n)
w=w/np.sum(w)

基于这组权重，我们可以得到投资组合的收益率和波动率。这里使用了NumPy的dot函数进行矩阵的乘法，代码如下：

# 投资组合收益率
p_ret= np.sum(df_new.mean()*w)*252
# 投资组合波动率
p_vol=np.sqrt(np.dot(w.T,np.dot(df_new.cov()*252,w)))

以上是针对一组资金权重w得到的收益率和波动率。

现在我们要找出一组权重，这组权重对应着最佳的收益风险比。首先，我们需要随机生成大量的权重，计算对应的投资组合收益率和波动率，进行初步观察，代码如下：

n=len(df_new.columns)
# 保存一系列权重对应的投资组合收益率
p_rets=[]
# 保存一系列权重对应的投资组合波动率
p_vols=[]
# 随机生成10000组权重
for i in range(10000):
    w=np.random.random(n)
    w/=np.sum(w)
    # 投资组合收益率
    p_ret= np.sum(df_new.mean()*w)*252
    # 投资组合波动率（需要注意的是，使用 np 生成的一维数据，实际上是N*1 矩阵，而不是1*N矩阵）
    p_vol=np. sqrt (np.dot (w.T,np.dot (df_new.cov() *252, w)))
    p_rets.append (p_ret)
    p_vols.append (p_vol)
p_rets=np.array (p_rets)
p_vols=np.array (p_vols)

在以上的代码中，我们得到了10000 个随机权重对应的收益率和波动率，现在将其绘制成图，代码如下：

plt.figure(figsize=(10,6))
plt.scatter(p_vols, p_rets, c=p_rets/p_vols,marker='o')
plt.grid(True)
plt.xlabel ('volatility')
plt.ylabel('return')
plt.colorbar (label='Sharpe ratio')

不同权重对应的收益率和波动率（夏普比率）如图所示：

在上图中，x轴对应着波动率，y轴对应着收益率。我们可以观察到，并不是所有的权重都能有良好的表现。对于固定的风险水平（比如0.25)，不同的组合有着不同的收益，同时存在着一个权重，可以有最好的收益（大概是0.23)。作为投资者，最关心的是固定风险水平下收益率的最大化，或者是固定收益率下风险的最小化，也就是所谓的有效边界。

最大化夏普比率

现在我们要找出使投资组合拥有最大夏普比率的资金权重。这是一个包含约束的最优化问题，首先需要建立一个函数，计算组合的夏普比率：

def portfolio_stat(weights):
    '''
    获取投资组合的各种统计值参数：
    weights:分配的资金权重
    返回值：
    P_ret:投资组合的收益率
    P_vol:投资组合的波动率
    P_sr:投资组合的夏普比率
    注意:rets是全局变量,在函数外部定义
    '''
    w = np.array (weights)
    p_ret = np.sum(rets.mean() * w)*252
    P_vol = np.sqrt (np.dot (w.T, np.dot(rets.cov()*252, w)))
    p_sr = p_ret/p_vol
    return np.array([p_ret, p_vol, p_sr])

这里定义了一个函数，输入是权重，输出是收益率、波动率和夏普比率。需要注意的是，函数内部使用的收益率数据rets是全局变量，由外部定义。
下面就来定义优化的目标函数，代码如下：

def min_func_sharpe(weights):
    # 优化的目标函数，最小化夏普比率的负值，即最大化夏普比率
    return -portfolio_stat(weights)[2]

该函数返回了夏普比率的负值，换句话说，我们需要对该函数进行最小化操作。之所以使用这种形式，是因为scipy.optimization 只有 minimize 函数（机器学习中优化目标通常是最小化损失函数）,所以这里使用了这种看起来有点奇怪的形式。
为了进行优化，我们需要使用scipy.optimize模块，代码如下：

import scipy.optimize as sco
# 有n个变量
rets = df_new
n = len(rets.columns)
# 优化的约束条件：资金的权重和为1
cons=({'type':'eq','fun':lambda x:np.sum(x)-1})
bnds=tuple((0,1) for x in range(n))
# 生成初始权重
w_initial = n*[1./n,]
opts_sharpe = sco.minimize(min_func_sharpe, w_initial, method='SLSQP',bounds=bnds,constraints=cons)
opts_sharpe

最后的 opts_sharpe 就是我们优化的结果。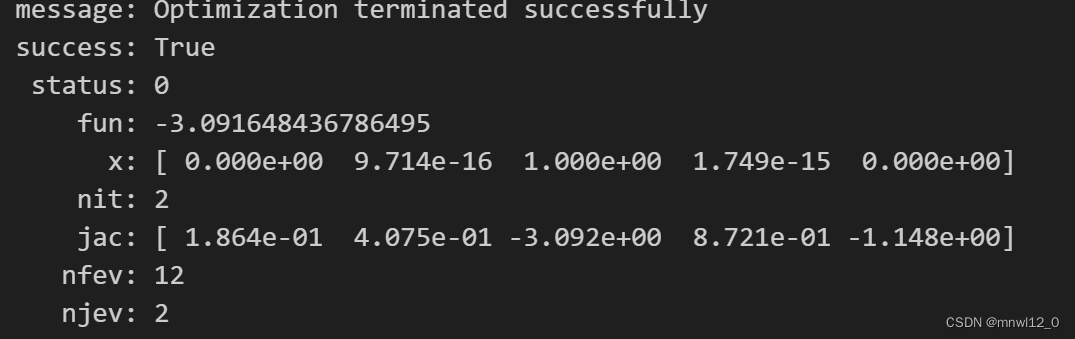

查看message 我们知道已成功优化。fun对应着优化后的函数值，也就是说，夏普比率为-3.1（有点惊人），对应的权重就是x的值。示例代码如下：

opts_sharpe['x'].round(2)

输出结果如下：

可以看到,除了s4权重为1，其他的都是0。这很明显，因为有三个策略的预期收益率是负值，权重置为0当然是最好的选择，s4和s6相比当然是把所有权重都给s4。

Black-Litterman 资金分配模型

MPT的优化矩阵算法

前面讲述了最大化夏普比率的具体操作流程，但仍有几个问题尚待解决。
为什么最大化夏普比率所带来的投资组合就是最优资金分配，最优的含义是什么？
即使最大化夏普比率所得到的组合的确是最优的，那么在生成的有效边界（efficient frontier）上是否还存在其他的投资组合收益，使得其风险收益比优于最大化夏普比率所带来的投资组合？
另外，投资者的效用函数是异质性的，那么最大化夏普比率对投资者的效用函数是否具有异质性表现。