目录
一、树的基本概念
（1）树的结点
（2）度
（3）结点层次
（4）树的高度
树的特点：
二、二叉树
（1）满二叉树
（2）完全二叉树
三、二叉树的存储
（1）顺序存储
(2)链式存储
四、二叉树的遍历
（1）前序遍历
（2）中序遍历
（3）后序遍历
（4）层序遍历
树是一种非线性的数据结构，存储具有“一对多”关系特点元素的一种数据结构。例如：组织架构、图书目录、商品种类、热点搜索词等。
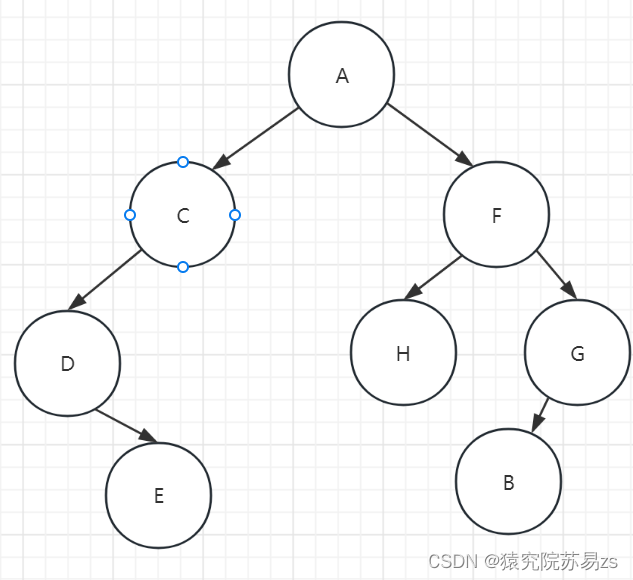
如图所示就是一个 树 ，对数据A来说，和数据C、F有关系；对于数据F来说，和数据H、G有关系。这就是“一对多”的关系。
将具有“一对多”关系的集合中的数据元素按照树的形式进行存储，整个存储形状在逻辑结构上看，类似于实际生活中倒着的树，所以称这种数据的存储结构称为“树”。
一、树的基本概念
树是一种非线性的数据结构，包含n个结点的有限集合，结点之间具备一对多的逻辑关系，当树的结点n=0时，该树被称为空树。
（1）树的结点
树结构中，存储的每一个数据元素都被称为树的“结点”。
结点又被细分为：根节点、子节点、叶子结点
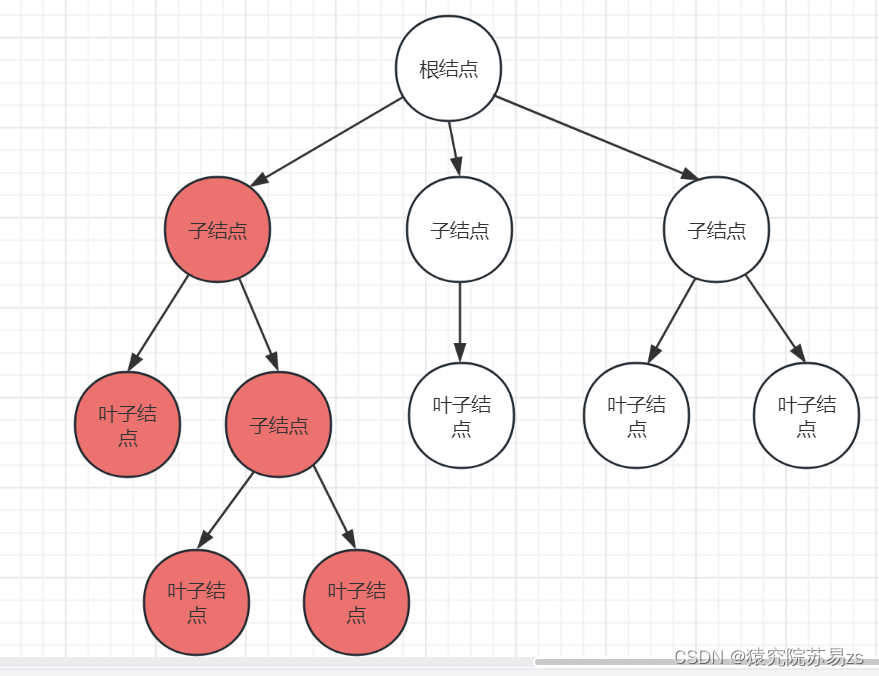
如图所示：叶子结点即树的末端结点，属于没有子结点的结点，统一称为叶子结点。
子树：由某个子结点作为根结点组成的树被称为子树。上图中红色部分就是一个子树。
（2）度
对于一个结点，拥有的子树个数（结点有多少分支）称为结点的度。
树的度：一颗树的度是树内各结点的度的最大值。
（3）结点层次
从一棵树的根结点开始，根结点所在层为第一层，根结点的子结点所在层为第二层，依次类推
（4）树的高度
一棵树的高度是树中结点所在的最大层次。树的高度，也被称为树的深度。
树的特点：
在任意一个非空树中，有以下特点：
1.有且仅有一个根结点
2.一棵树中的任意两个结点，有且仅有唯一的一条路径连通，不存在回路。
3.一棵树如果有n个结点，那么它一定有n-1条边
二、二叉树
二叉树是一种结点的度不大于2的有序树，子结点通常被称为“左孩子结点”和“右孩子结点”。
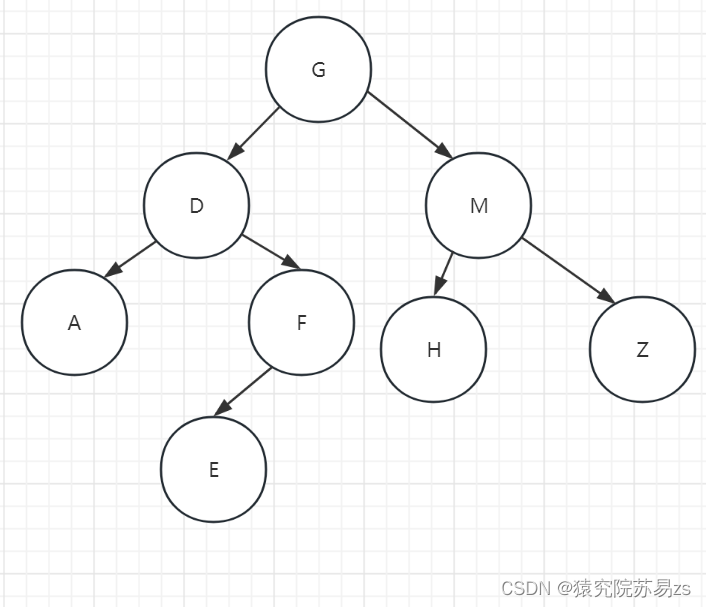如图所示就是一个二叉树
这个图中树的度为3，所以此树就不是一个二叉树
二叉树又被分为满二叉树和完全二叉树
（1）满二叉树
满二叉树是一种特殊的二叉树，它的所有非叶子节点都存在左右子结点，并且所有的叶子结点都在同一层级
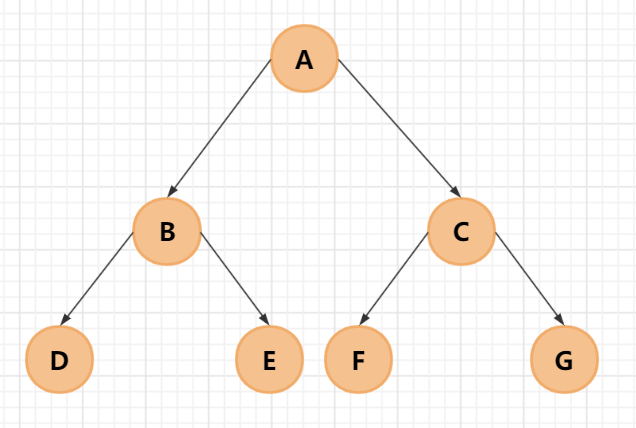
满二叉树的特点：
（2）完全二叉树
如果二叉树中，从根结点到倒数第二层，符合满二叉树要求，其叶子结点可以不完全填充，但必须靠从左到右连续分布，这样的二叉树被称为完全二叉树。
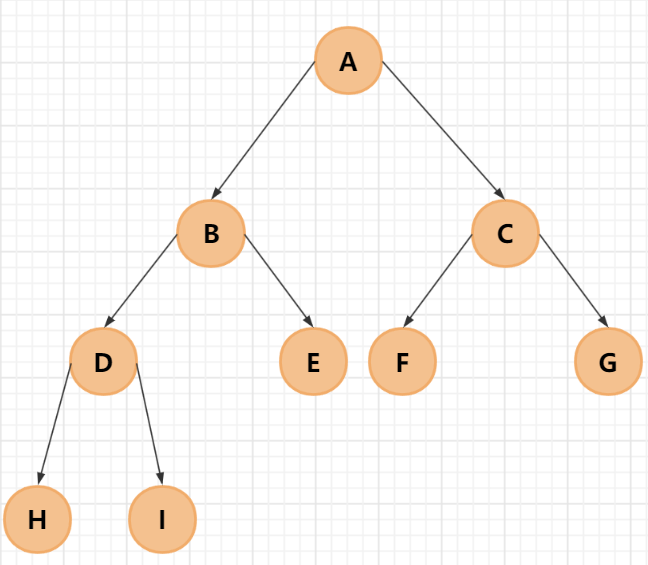
三、二叉树的存储
（1）顺序存储
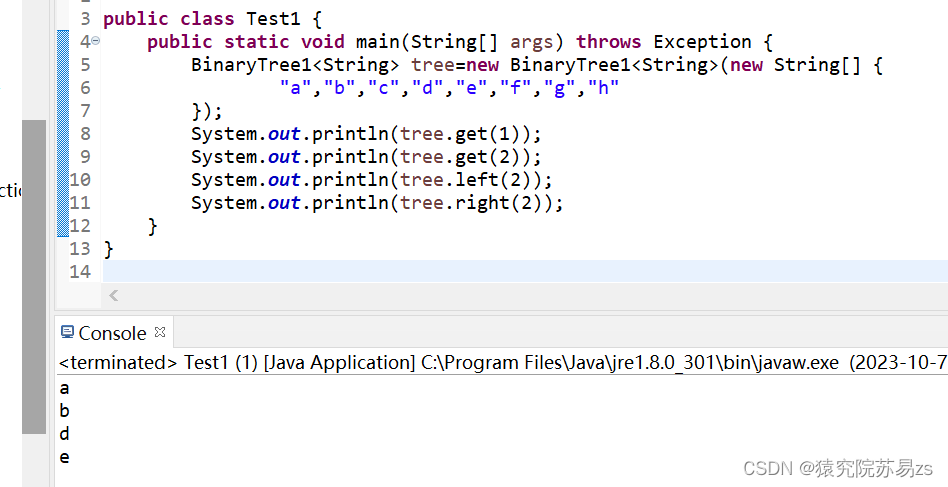
顺序存储指的是使用顺序表（数组）存储二叉树。但是顺序存储只适用于完全二叉树。满二叉树也是完全二叉树，所以同样适用。
在顺序存储中，顺序表中的每一个位置仅存储结点的data，不需要存储左右子结点的指针，子结点的索引通过计算父结点下标完成。
如果一个父结点的下标为parentIndex它的左结点下标为：2parentIndex, 右子结点下标为：2parentIndex+1
如果完全二叉树，使用数组顺序存储，可以完全利用数组空间
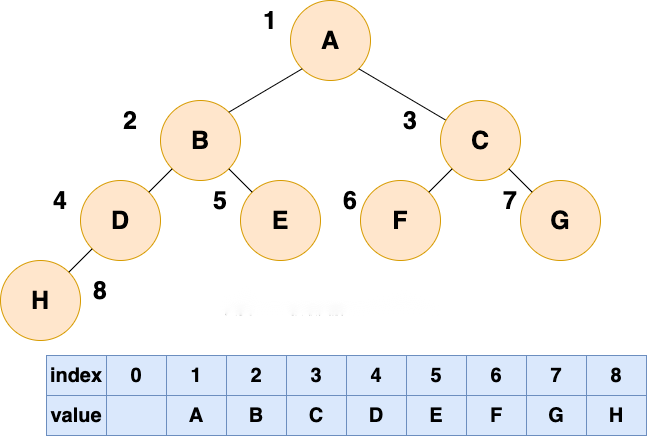
如果是普通二叉树，使用数组顺序存储，在数组中就会出现空隙，导致内存利用率降低
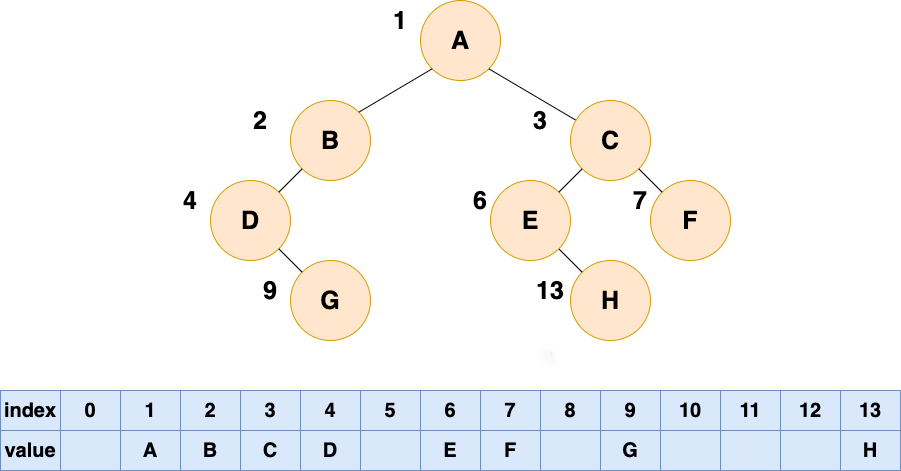
//基于数组（顺序存储）的二叉树
public class BinaryTree1<E> {
// 创建一个新的空数组用来存储二叉树
private Object[] elementData=null;
// 进行初始化操作
public BinaryTree1(E[] elements) {
// 新数组的长度要比放入数据的数组长度大一个，因为新数组中从下标为1开始存储
elementData=new Object[elements.length+1];
for(int i=0,index=1;i<elements.length;i++,index++) {
elementData[index]=elements[i];
}
}
// 获取指定下标处的元素
public E get(int index) {
return (E) elementData[index];
}
// 获取指定下标的左孩子
public E left(int index) throws Exception {
// index<<1 即2倍的index，一个子节点的下标的二倍是他的左孩子结点，如果2倍的index大于等于数组长度则没有左子孩子
if((index<<1)>=elementData.length) {
throw new Exception("没有左孩子");
}
return (E) elementData[index<<1];
}
// 获取指定下标的右孩子
public E right(int index) throws Exception {
if((index<<1)+1>=elementData.length) {
throw new Exception("没有右孩子");
}
return (E) elementData[(index<<1)+1];
}
}
(2)链式存储
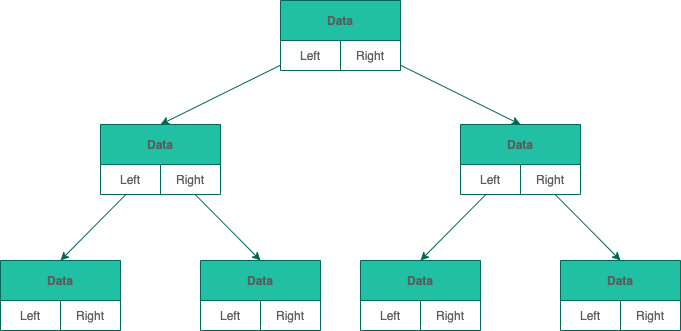
二叉树的链式存储依靠指针将各个结点串联起来，不需要连续的存储空间。
每个结点包括3个属性：
- 数据 Data
- 左孩子结点指针 Left
- 右孩子结点 Right
//二叉树的链式存储
public class BinaryTree<E> {
// 根节点
TreeNode<E> root;
public BinaryTree(E val) {
root=new TreeNode<E>(val);
}
// 结点类
static class TreeNode<E>{
E data;
TreeNode<E> left;
TreeNode<E> right;
public TreeNode() {
}
public TreeNode(E val) {
this.data=val;
}
}
public TreeNode<E> left(TreeNode<E> parent,E val){
TreeNode<E> newNode=new TreeNode<E>(val);
parent.left=newNode;
return newNode;
}
public TreeNode<E> right(TreeNode<E> parent,E val){
TreeNode<E> newNode=new TreeNode<E>(val);
parent.right=newNode;
return newNode;
}
}四、二叉树的遍历
| 前序遍历 | 根结点->左子树->右子树 |
| 中序遍历 | 左子树->根结点->右子树 |
| 后序遍历 | 左子树->右子树->根结点 |
（1）前序遍历
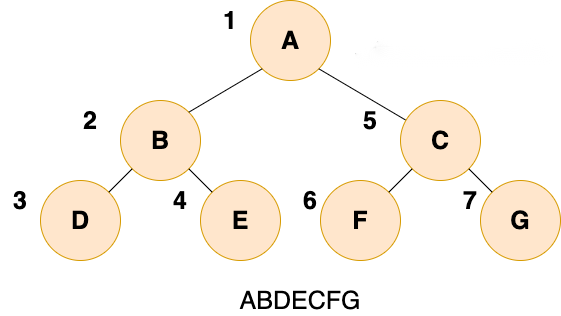
public static void preOrder(TreeNode root) {
if(root==null) {
return;
}
System.out.print(root.data);
preOrder(root.left);
preOrder(root.right);
}（2）中序遍历
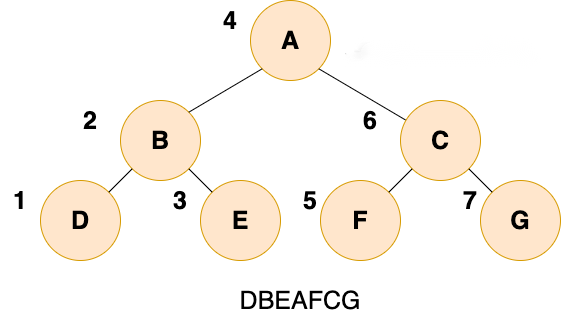
public static void inOrder(TreeNode root) {
if(root==null) {
return;
}
inOrder(root.left);
System.out.print(root.data);
inOrder(root.right);
}（3）后序遍历
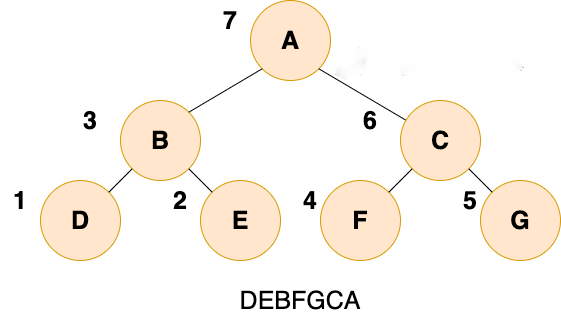
public static void postOrder(TreeNode root) {
if(root==null) {
return;
}
postOrder(root.left);
postOrder(root.right);
System.out.print(root.data);
}（4）层序遍历
层序遍历，就是按二叉树从上到下，从左到右，依次打印每层中每个结点存储的数据
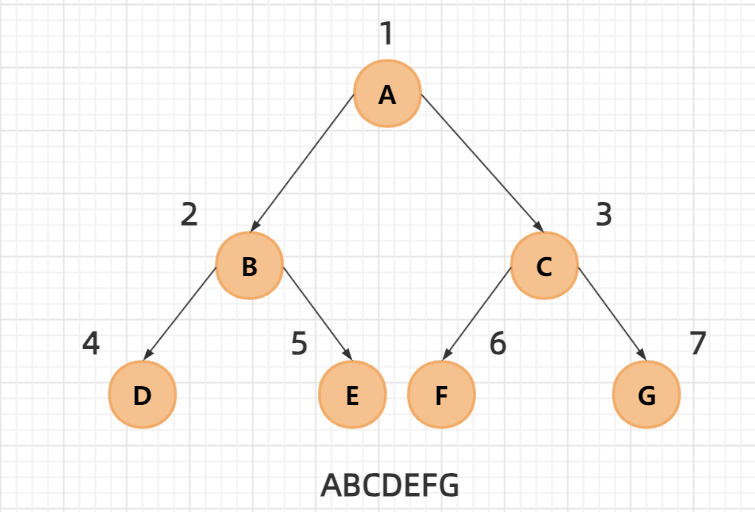
public static void levelOrder(TreeNode root) {
if(root==null) {
return;
}
Queue<TreeNode> queue=new LinkedList<TreeNode>();
queue.offer(root);
while(true) {
TreeNode t=queue.poll();
if(t==null) {
break;
}
//访问当前节点，就用打印表示访问即可
System.out.print(t.data);
if(t.left!=null) {
queue.offer(t.left);
}
if(t.right!=null) {
queue.offer(t.right);
}
}
}五、二叉查找树
二叉查找树也称为二叉排序树，即BST，是一种特殊的二叉树，它具备以下特点：
1、若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值
2、若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值。
3、左、右子树也分为二叉排序树
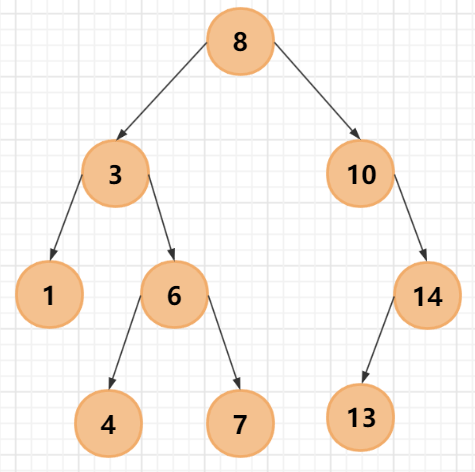
二叉查找树的优势在于可以快速查找。
（1）二叉查找树的基本结构
public class BST {
// 根结点
TreeNode root;
// 树内部类
static class TreeNode{
Integer data;//结点数据
TreeNode left;//左子结点
TreeNode rigth;//右子结点
TreeNode parent;//父结点
public TreeNode() {
}
public TreeNode(Integer val) {
this.data=val;
}
}
}
（2）插入结点实现
// 插入新结点
public void insert(TreeNode newNode) {
// 默认使用根结点
TreeNode currentNode=this.root;
// 新结点的父结点
TreeNode parentNode=null;
// 查找新结点的父结点
while(currentNode!=null) {
parentNode=currentNode;
if(newNode.data>currentNode.data) {
// 右
currentNode=currentNode.right;
}else {
// 左
currentNode=currentNode.left;
}
}
// 设置新结点的父结点
newNode.parent=parentNode;
// 判断当前树是否为空树
if(parentNode==null) {
this.root=newNode;
}else {
// 保存新结点
if(parentNode.data<newNode.data) {
parentNode.right=newNode;
}else {
parentNode.left=newNode;
}
}
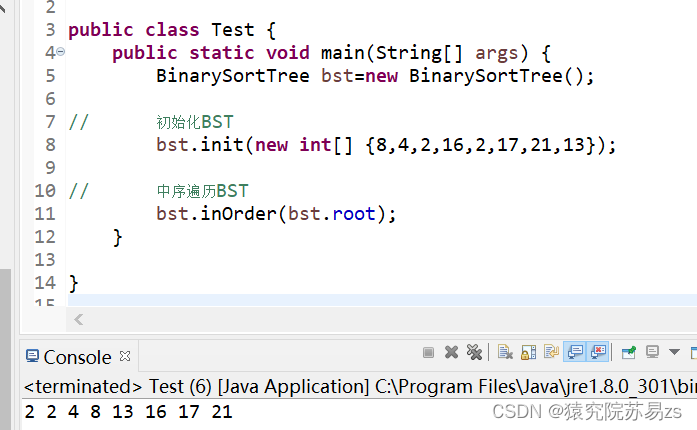
}（3）初始化BST
public void init(int[] array) {
for(int n:array) {
insert(new TreeNode(n));
}
}
（4）查找结点
// 查找结点
public TreeNode search(TreeNode parentNode,int data) {
if(parentNode==null) {
return parentNode;
}
if(data<parentNode.data) {
return search(parentNode.left,data);
}else if(data>parentNode.data){
return search(parentNode.right,data);
}else {
return parentNode;
}
}（5）查找最大值
// 查找最大值
public TreeNode findMax(TreeNode currentNode) {
if(currentNode==null) {
return currentNode;
}
TreeNode parent=null;
while(currentNode!=null) {
parent=currentNode;
currentNode=currentNode.rigth;
}
return parent;
}
