AB试验（五）实验过程中的一些答疑解惑

实验结果不显著怎么办

出现实验结果不显著的原因

A/B测试的变化确实没有效果，两组指标在事实上是相同的
A/B测试的变化有效果，但由于变化的程度很小，测试灵敏度power不足，所以没有检测到两组指标的不同

如何解决

第一种原因一般选择放弃这个变化，尝试测试新的变化
对于第二种原因，尝试提高power：通过样本量公式 $n=\frac{(Z_{1-{\frac{\alpha}{2}}}+Z_{1-\beta})^2}{(\frac{\delta}{\sigma_{pooled}})^2}=\frac{(Z_{1-{\frac{\alpha}{2}}}+Z_{power})^2}{(\frac{\delta}{\sigma_{pooled}})^2}$ ，可以发现提高样本量或者减小方差即可。
- 通过样本量提高power
  - 延长测试时间：每天产生的样本量是一定的，所以当测试时间延长后，收集到的样本量就会扩大
  - 增加测试使用流量在总流量中的占比
  - 多个测试共用同一个对照组：实际中会同时进行多个实验，有些实验的对照用户基本一样。假设有4个同时进行的实验，每个实验两组，可用流量有8w，则每组只能使用1w的流量，但将四个实验共用同一个对照组，此时的实验就变成了A/B/n，只有5组，则每组可使用的流量就达到了1.6w。
    
    经验建议：如果时间允许，最常用的是延长测试时间，简单实用。如果时间不充足，则可以优先选择增加测试使用流量占比。如果实际中存在多个实验的对照组相同的情况下，可以进行A/B/n实验
- 通过减小方差提高power
  - 保持原指标不变，通过剔除离群值（Outlier）减小方差：如果指标的直方图分布中有明显的异常值，可以通过设置封顶阈值(Capping Threshold)的方式。例如只选取95%的取值范围，剔除剩余的5%的离群值。由于会存在极少数特别活跃的用户，他们产生的行为数据往往就会显得异常。
  - 选用方差较小的指标：取值范围窄的指标比取值范围广的直销方差要小，常见的概率类指标比均值类指标方差小，均值类指标比数量的方差要小。例如购买额>人均购买额>购买率
  - 倾向得分匹配（PSM）：构造与对照组相似的数据点，当两组样本越相似，方差越小
  - 在触发阶段计算指标：一般出现在有固定路径的业务场景，例如电商的购买：进入APP->浏览商品->查看商品详情->加入购物车->购买。当优化整个路径时，往往用户在进入APP就被分配到了实验组/对照组，在后续测试购物车页面变化时，只有进入到购物车页面的用户才能出发测试条件进入实验。

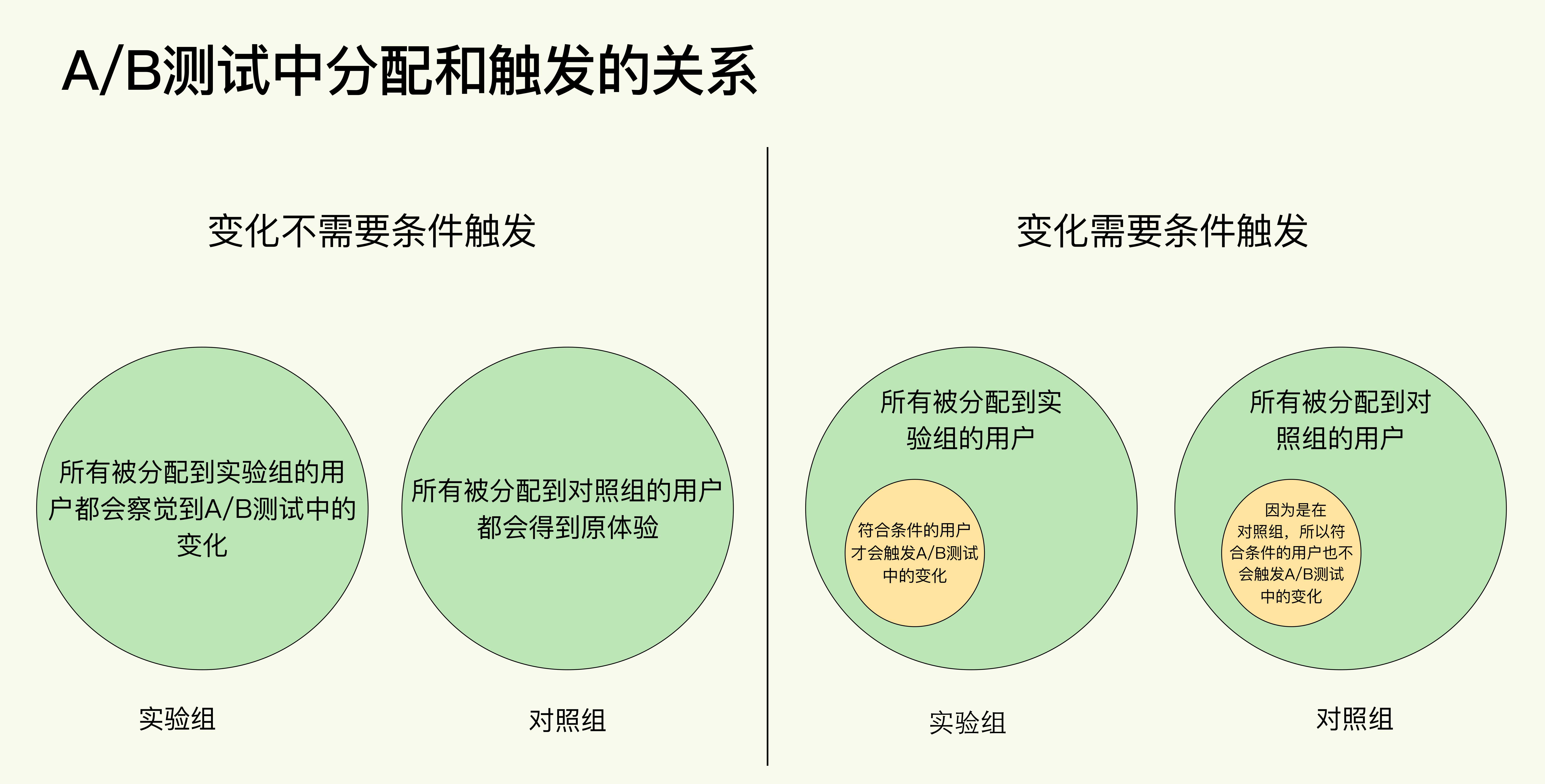
多重检验问题

定义

指的是当同时比较多个检验时，第一类错误率α就会增大，而结果的准确性就会受到影响这个问题

产生的结果

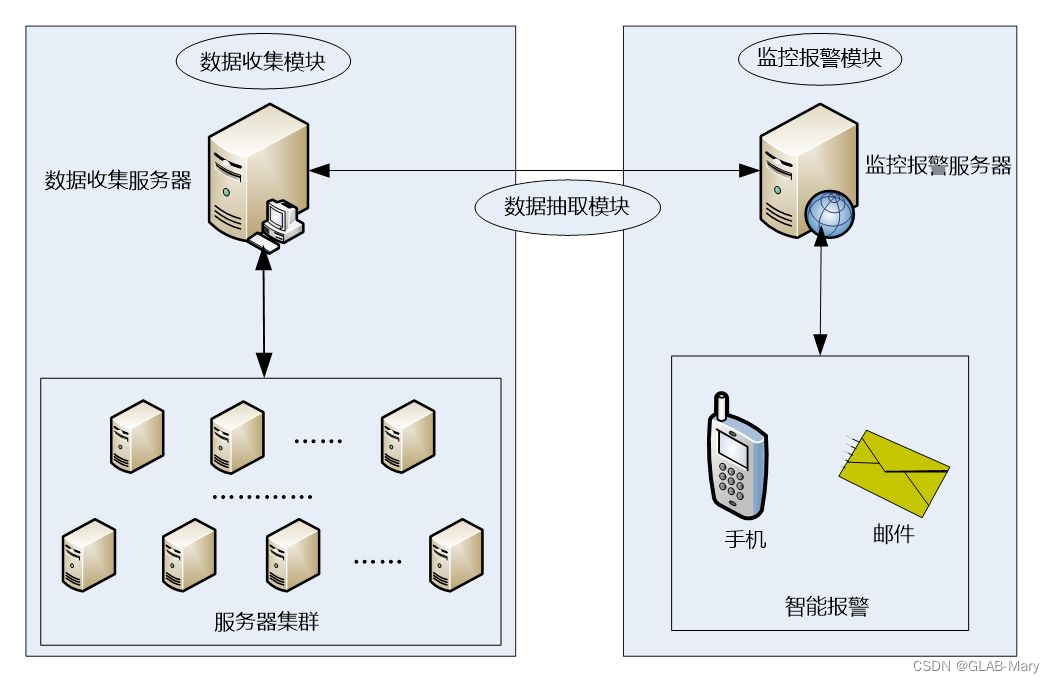
当我们进行一次实验时，往往存在5%的概率（犯第一类错误）认为两组指标不同，但事实上两组指标相同。如果进行多次重复实验，例如20次，假设每次实验依然存在犯第一类错误的概率为5%，那20次中至少出现一次第一类错误的概率约为 $1-(1-0.05)^{20}=64\%$ 。这里的概率p（至少出现一次第一类错误的概率）又叫FWER（Family-wise Error Rate）。

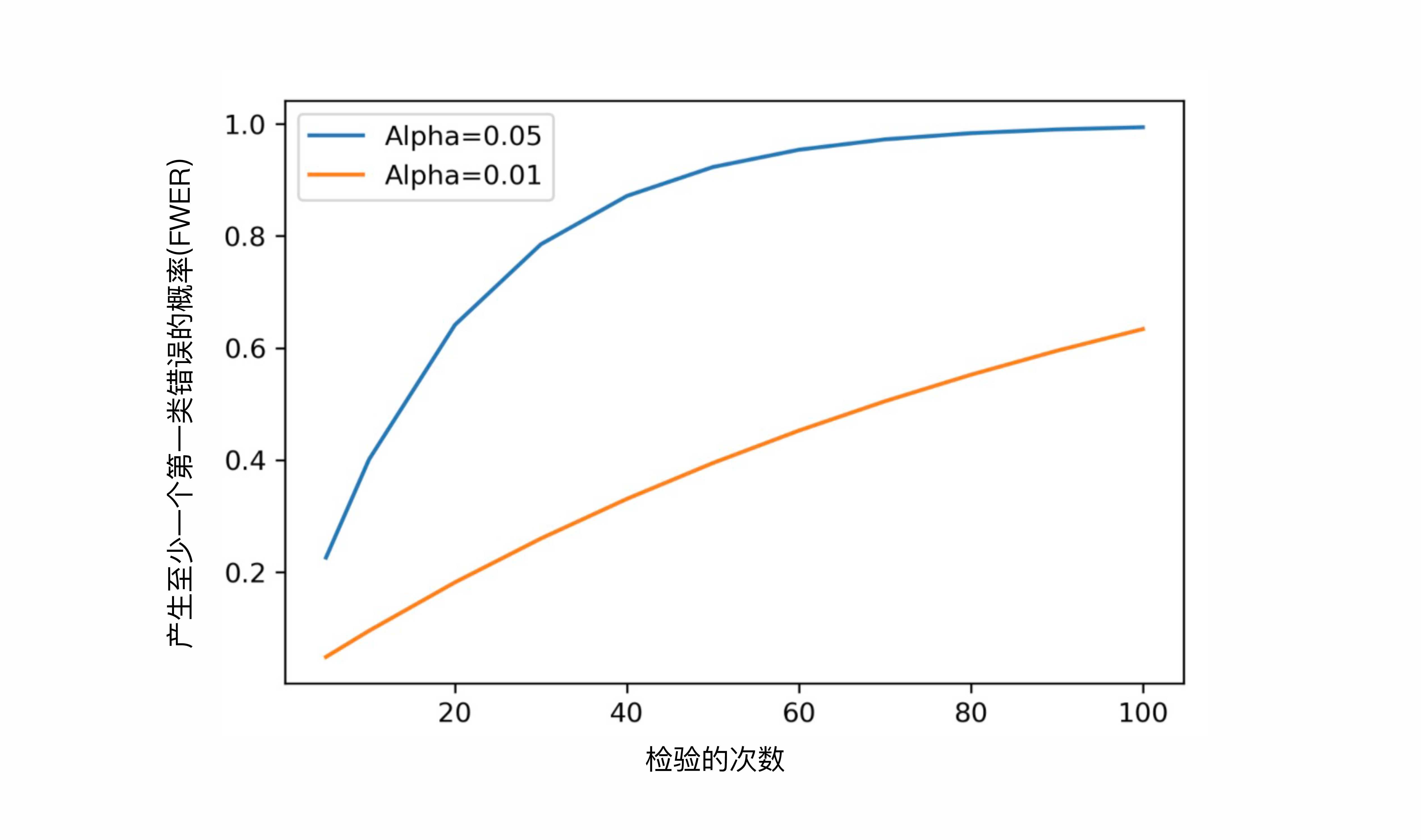
由上图可知：

随着检验次数的增加，FWER会显著升高
当 $\alpha$ 越小时，FWER会越小，上升的速度也越慢。所以降低 $\alpha$ 就成为了解决多重检验问题的一种潜在有效方法

产生多重检验问题的原因

当A/B测试有不止一个实验组时：即在进行A/B/n时，会同时进行n个检验
当A/B测试有不止一个评价指标时：多个指标往往会进行多次检验
当你在分析A/B测试结果，按照不同的维度去做细分分析(Segmentation Analysis)时：有时因为业务需要，会对一些维度下钻比较实验结果，例如一次实验包含了全球多个国家，当分析每个国家的测试结果时就会进行多次检验
当A/B测试在进行过程中，你不断的去查看实验结果：由于实验一直在进行，每次累计的样本都不一样，每次查看实验结果都相当于一次检验

如何解决多重检验问题

保持每个检验的p值不变，调整 $\alpha$ ：通过Bonferroni校正(Bonferroni Correction)，简单就是把 $\alpha$ 变成 $\alpha/n$ 。n是检验的个数。比如 $\alpha=5\%$ ，当进行20个检验时，校正的 $\alpha=5\%/20=0.2\%$ ，此时的 $FWER=1-(1-0.25\%)^{20}=4.88\%$ ，与当初设定的 $\alpha=5\%$ 差不多。该方法简单易操作，但对于不同的p值都采取了一刀切，显得比较保守，在检测次数较少的时候比较适用。当检测次数较大时（例如上百次，常出现在维度细分场景下），Bonferroni校正会显著增加第二类错误率 $\beta$ ，因此通常会通过调整p值的方法
保持 $\alpha$ 不变，调整每个检验的p值：常用的方法是通过控制FDR（False Discovery Rate）来实现。这是一类方法，比较常用的是BH法(Benjamini-Hochberg Procedure)。BH法会考虑到每个P值的大小，然后做不同程度的调整。大致的调整方法就是把各个检验计算出的P值从小到大排序，然后根据排序来分别调整不同的P值，最后再用调整后的P值和α进行比较
实践中，通常使用Python中的multipletests函数，该函数包含各种校正多重检验的方法，包括Bonferroni校正和BH法，我们使用时只需要把不同的p值输入，选取校正方法，这个函数就会给我们输出校正后的p值

经验总结：虽然Bonferroni校正十分简单，但由于过于严格和保守，所以在实践中更推荐使用BH法来矫正p值

学习效应

定义

一些实验中的变化是非常明显的（例如交互界面、功能模块等），由于老客户在过往历史已经习惯了就的交互界面或功能，对于新的变化需要一段时间来适应和学习。因此老用户在这个适应学习阶段的行为表现与平常表现不一致。

产生的结果

新奇效应：老用户对新变化具有积极的反应，受较强的好奇心驱使去尝试。因此短期内评价指标会有明显提升，但当老用户适应了此次变化后，评价指标又开始回到之前的水平
改变厌恶：老用户对新变化具有消积的反应，产生较强的抵触情绪。因此短期内评价指标会有明显降低，但当老用户适应了此次变化后，评价指标又开始回到之前的水平

如何判断是否存在学习效应

监控评价指标随时间的波动：在没有学习效应的情况下，评价指标是稳定的。如果指标在实验开始迅速提高，然后随着时间趋于稳定，则存在新奇效应；如果指标在实验开始迅速降低，然后随着时间趋于稳定，则存在改变厌恶
对比实验组和对照组中的新用户：如果评价指标在新用户中没有显著结果，但在总体上显著的，表明这次变化只对老用户产生了影响，因此大概率存在学习效应

如何剔除学习效应的影响

延长实验时间，等到实验组的学习效应消退后再进行比较

辛普森悖论

定义

当多组数据内部组成分布不均匀时，从总体上比较多组数据和分别在每个细分领域中比较多组数据可能会得出相反的结论。举个房价的例子：2020年的房价较2019年降低了7%！实际上新房和二手房的成交价都是上涨的

	新房成交数量	新房成交均价	二手房成交数量	二手房成交均价	成交均价
2019年	10w	3w	2w	1w	2.7w
2020年	2w	5w	10w	2w	2.5w

实验中产生辛普森悖论的原因

在分流过程中，实验组和对照组在个别细分维度的分布不一致

如何解决辛普森悖论

在实验开始前，进行AA测试，对测试结果进行特征分布相似的合理性检验，如果一直检验到某个维度存在问题，则需要提BUG给研发进行排查解决，直到通过了特征分布相似的合理性检验为止
如果没有充足的时间或者已经产生了结果，可尝试PSM构造相似的实验组进行结果比较。如果分布差异较大导致没有足够的样本进行PSM，则以细分领域的结果为准，整体结果不能作为参考

实验组和对照组不独立

定义

A/B测试有一个前提，实验组和对照组的实验单位是要相互独立的，这个前提又叫做SUTVA（ Stable Unit Treatment Value Assumption）。测试中各组实验单位的行为仅受本组体验的影响，不能受其他组的影响。

破坏两组独立性的表现形式

社交网络/通讯类业务：典型的如微信、微博、领英、语音/视频通讯、电子邮件等。例如在实验组的用户A收到新算法推荐的内容，看到了更多喜欢的内容从而提高了使用时间，也就提高了该用户的分享和推荐。恰巧用户A的好友分流在了对照组，即使他没有收到新算法推荐的内容，但如果受到用户A的分享内容后也可能花更多的时间在此APP上。因此实验组的用户通过社交网络关系影响到对照组用户的行为，从而两组的人均使用时长都有了提升。
共享经济类业务：一般是平台型业务，供给双方均是用户。典型如淘宝、滴滴、共享单车等。由于供需关系是动态平衡的，一方的变化必然会引起另一方的变化。例如某打车APP优化了用户的打车流程，使得用户打车变得更容易。在实验组的用户因为收到优化后的打车流程，打车更容易，所以流入实验组的司机更多，但司机的数量是一定的，这就导致流入对照组的司机更少了，进而造成对照组的用户打车更难，体验也更差了。所以该实验的结果往往高估了实验组的优化结果。
共享资源类业务：有些共享资源类业务是有固定的资源或预算，典型的如广告营销。例如在固定100w的广告预算下，实验组的广告如果更好，就会产生更多的点击，由于当前的线上广告常常以点击收费，导致实验组的广告花费更高。因此对照组的预算就会被实验组抢占，其实验结果自然会受到影响。

如何避免两组独立性被破坏

从地理上隔离：常用于具有线下业务的场景，例如共享出行/租赁等。可以选取相似的两个城市的用户作为实验/对照组，城市的发展、经济、文化、人口以及该业务在该城市的渗透率等应尽可能相似。
从资源上隔离：常用于共享资源类业务，例如在广告营销中固定两组的预算，使得两者的预算比例一样。
从时间上隔离：常用于不易被用户察觉的变化上，例如算法优化。对同一拨用户，测试他们在不同时间上的结果。时间应尽可能的相似，例如都是周中、都在上午等。
通过聚类隔离：常用于社交网络类业务，根据用户的交流程度进行聚类，将有关联的用户聚成一个cluster，每个cluster作为一个实验单位随机分组。这样能一定程度上减少不同组之间的干扰，不过该方法比较复杂，实施难度大，且需要算法和工程团队支持。

经验总结：通过不同形式的隔离来排除两组之间的干扰

不适合进行A/B测试的场景

有哪些场景不适合A/B测试

无法控制测试变量：有些变量是用户的个人选择，团队能控制的变量只能存在于产品/业务端，对于用户的个人选择是没法控制的。例如想了解用户从QQ音乐换到网易云后的人均使用时长，这里的变化就是用户更换APP。这种用户自主行为是无法控制的，及时进行营销干预也会产生偏差，使得测试结果不准确
重大事件发布：典型的如新品发布等大成本营销活动，如果只触及小部分用户是明显不符合利益的。又如更改商标等涉及公司形象的事件，如果进行小流量测试会造成多个商标同时在市场流通，造成用户困扰，不利于公司形象打造。

解决方案

倾向得分匹配（PSM）：根据历史数据人为构造两组相似的样本，进行观察性研究。
用户研究
- 深度用户体验研究：例如通过用户眼球运动来追踪用户选择过程的眼动研究或者用户自己记录的日记研究
- 焦点小组：有引导的组织用户进行小组讨论
- 调查问卷：预设好问题和选项并做成问卷发放给潜在用户，然后收集结果进行分析