Hi,你好。我是茶桁。
我们在机器学习入门已经学习了两节课,分别接触了动态规划,机器学习的背景,特征向量以及梯度下降。
本节课,我们在深入的学习一点其他的知识,我们来看看K-means.
当然,在本节课我们也只是浅尝即止,关于这些内容,后面我们还有更详细的内容等着我们去深入学习。
淘宝的商品问题
上节课的最后,我们学习的内容是梯度下降,在这里不得不再次强调一下,梯度下降是咱们以后非常非常重要的一个内容。
那关于今天要讲的K-means呢,我们还是按照惯例,用一个问题来引入。这个问题也是一个实际问题,并非乱举例。
在淘宝国际上经常会有一些人,基本是境外人员,会从国外出售违禁商品,国家是不许卖的,这些东西会被要求全部下架。
这些人就有一个很聪明的方法,他会更换物品的名字。
比方枪支又叫狗子,或者叫什么野狗。赌博账号叫米科,毒品账号可以叫野狼等等。
我们把这些话称为黑话、黑词。我们在明处、他们在暗处。整个淘宝假设现在就只知道十几个、二十几个人黑话,想屏蔽他们就很难屏蔽。
有人就说,我们可以像拦截垃圾邮件一样,我们可以去做记忆训练。
但是这个时候就有一个情况,你做那个垃圾邮件的时候会发现有很多很多的垃圾邮件可以供你训练,但是在互联网上,这种暗语可能有几千上万,但是在整个淘宝里边,他特别的少,比例特别低,其次经常还会变。也就是我们经常会说到的时效性。
后来人们想了一个这样的方法:
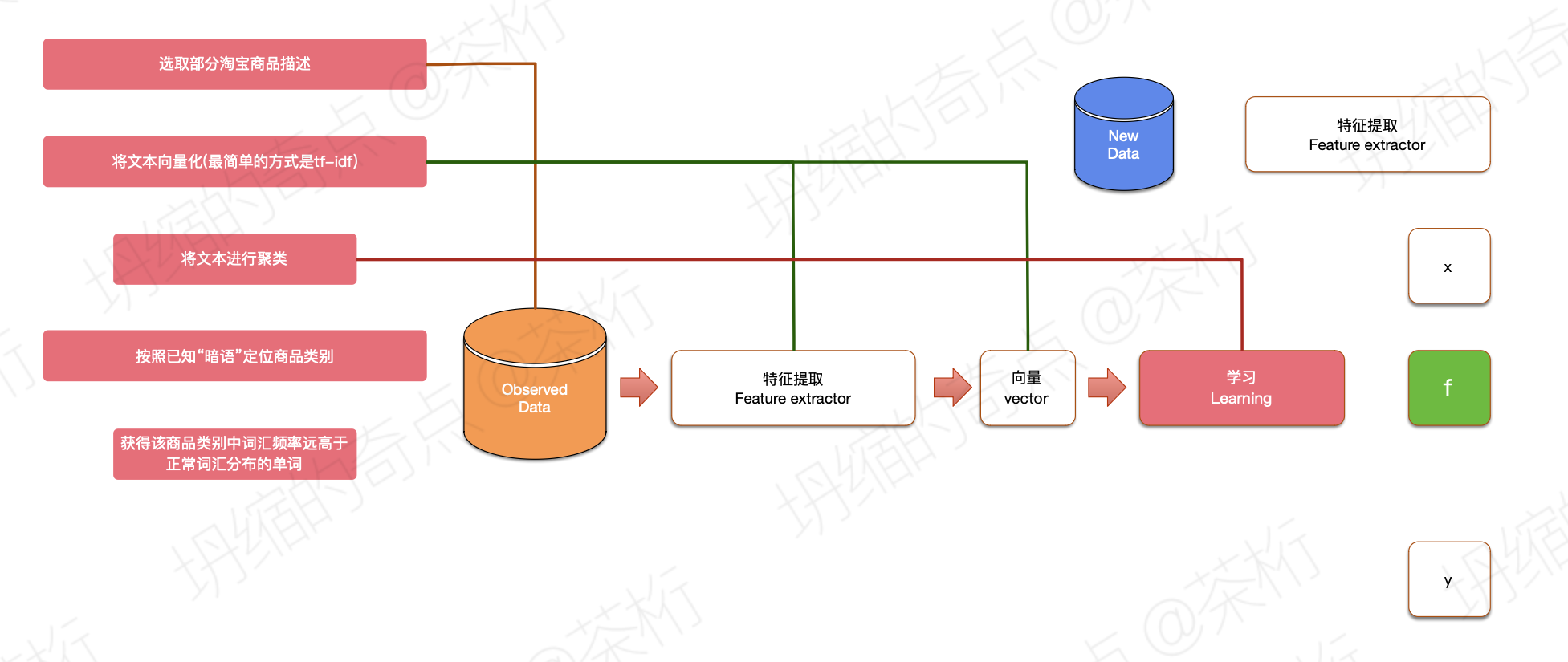
第一步选取部分淘宝的商品描述,第二步将文本向量化,也就是把一个一个的文本给它变成一个一个向量。接下来对文本进行聚类。
之前我们说过,聚类其实没有标准答案。我们就让它聚三类、聚四类、聚五类,可以规定聚多少类。把非常非常多的向量,距离接近的这些向量归为一类。所以对应出来把文本向量化之后,就是把文本接近的词归为同样一类。
然后我们按照已知的暗语定位商品的类别,获得该商品下词汇频率远高于正常词汇分布的单词。
比如我们知道“野狗”这个单词是一个黑词,首先让在淘宝里的这些商品进行自由分类,让文本相似的聚集到一块,然后我们看一下包含了”野狗“这个单词这个商品的那一大类里边哪些单词出现的频率比正常情况下出现的高。
就是说,如果这个人爱说黑话,那么他所说的别的话也更有可能是黑话。
假如说有一些街头帮派的人,他们爱说一些你听不懂的话,那么你听到了一句这样的话就找到了这样的这个人。把这一类人找到,再每天去监听一下他们说了什么话,他们说的有些话的频率其实比正常情况人群说的高,大概率就是黑话。
看这个过程,其实对应了我们上一节说说的,机器学习的基本框架。有观察的部分,有提取特征的部分,还有让机器进行聚类,让他去学习的过程。
这个时候我们又发现,让机器自动去聚类之后我们并没有用那个最终求解出来的f。也就是我们并没有让它去预测新数据,是用老数据,然后让老数据去给它聚类,并没有让这个东西去预测新数据。
其实我说两个非常重要的工程经验。
第一个工程经验是,所谓算法工程师并不是说他记住了多少算法,而是他要能把一个实际问题抽象成一个算法问题。
就比方说淘宝的这个问题,如果没人告诉你的话,你并不知道他是一个聚类问题。另外一些人,就能想到可以用聚类这个方法去解决。这个其实才是最重要的。
我有很多同学,记住了很多但是不会应用,这就不行。
第二个重要的点是在真正的工作中,我们的机器学习方法很多时候是作为整个项目的一部分,单靠机器学习很难解决完整项目。
整个项目它可能很长,有十多步,其中有几步用到了机器学习。而且用到的还是机器学习的中间的一些部分。
假如我们现在选10万个淘宝的商品,对他进行了聚类。其实按照标准的机器学习过程,聚类完成之后得再学些新的商品,让现在这个模型对这些新的去进行分类。
但是我们没有进行这一步,我们把这10万给它分完类,自动聚完类之后就停了,就进行下面的工作了。这就说明机器学习这个完整的步骤完全可以只使用其中的某几个部分,而不是一定要把这个全程跑完。
这就是要做一个算法工程师很重要的点。
K-means
接下来,来看第一个机器学习算法问题。我们把第一个机器学习问题叫做K-means。
如果给出了很多个点,给出了很多个向量。我们拿比较方便看的二维向量举例。
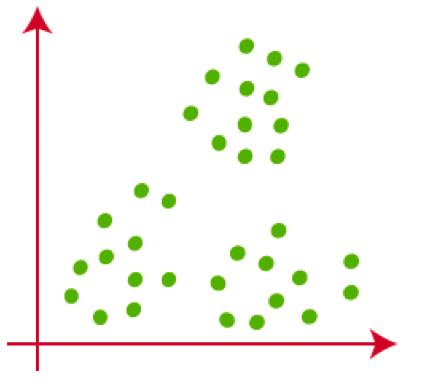
K-means原理很简单,假如有这么些数据。虽然我不知道最终的分类的结果是什么样的,但是可以告诉你我想把这些数据分成几类。
假如现在我要把这个数据分成三类,那么就随机产生3个点。
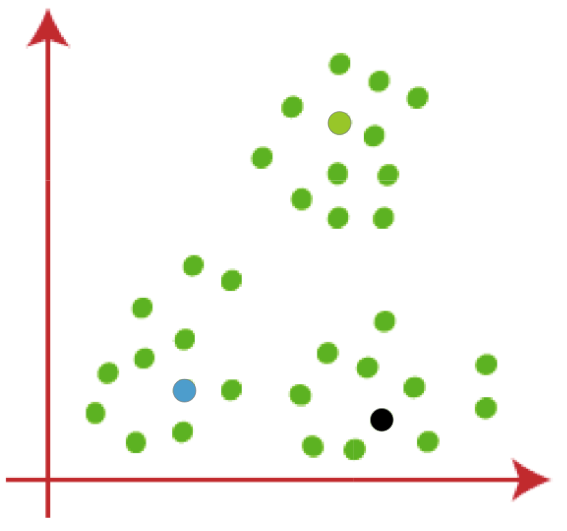
第一步是随机产生k个点。
第二步,判断其余待分类的点,离我们随机的K点哪一个更近一点。每一个待分类点一定能找到一个离的更近的k点。
然后把每一个分类的里面点再重新求一下它的中间值。
求得了新的中间值之后,把这个新的中间值再做为刚才的k点,让里边的所有的点去选择到底离哪个k最近。
然后再产生一轮新的k,当一轮新的k和上一轮的k的距离很接近的时候,我们就说找到了,这个中心点基本上就不变了。我们把这个方法叫做K-means。
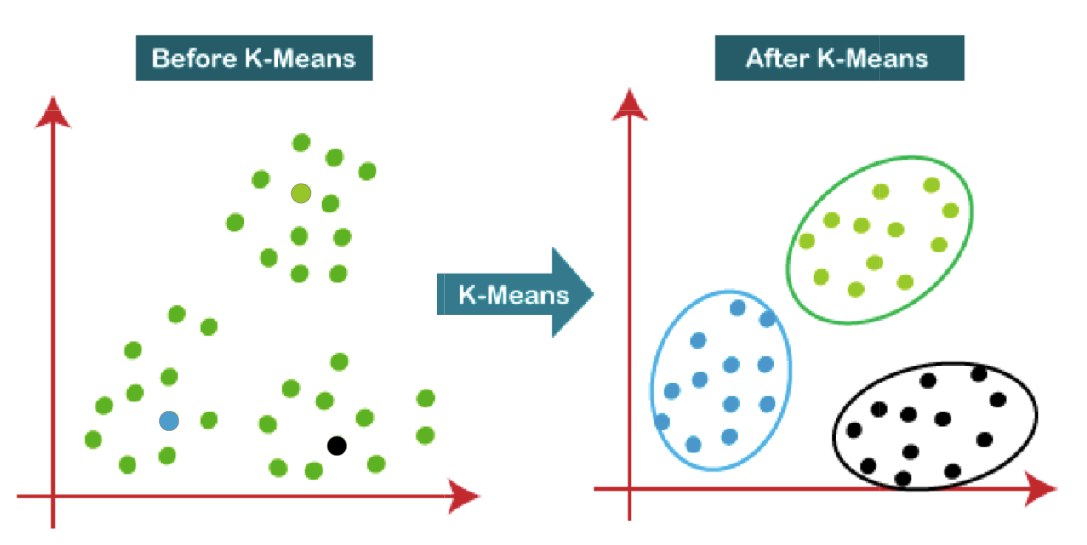
这个means就是平均值的意思,首先有k个点,然后把这个图像里面的所有的点分配到这k个点,找到离k个点里面最近的。然后把这些隶属于每个k点最近的点求平均值,也就是求他的中心点。
求完中心点,这个中心点又变成了新的k值。同样的我们再执行,找离k最近的那些点,再求平均值。
这样一轮一轮的,把k点这样求出来之后,当上一次的k和这一次的k不怎么变的时候,我们就找到了它的中心值,就把它聚类起来。我们就把它叫做K-means。
以上是K-means的原理,接下来,咱们来看一个实际的案例。比如说,咱们想这样一个场景,我们给中国建几个能源中心,给咱们中国的省会设置能源中心。
OK,我们来看一下, 那首先呢,我们需要一组数据。
coordination_source = """
{name:'兰州', geoCoord:[103.73, 36.03]},
...
{name:'澳门', geoCoord:[113.54, 22.19]}
"""
完整数据请查看我源代码
Core foundations/07.ipynb,为了篇幅我这里就不放完整的了。
这组数据就是每个省的城市和坐标,我们用正则表达式把这个城市里的名字和数字地址全部找出来。
import re
# 创建变量保存
city_location = {
'香港': (114.17, 22.28)
}
test_string = "{name:'兰州', geoCoord:[103.73, 36.03]},"
pattern = re.compile(r"name:'(\w+)',\s+geoCoord:\[(\d+.\d+),\s(\d+.\d+)\]")
for line in test_string.split('\n'):
city_info = pattern.findall(line)
if not city_info: continue
# following: we find the city info
city, long, lat = city_info[0]
long, lat = float(long), float(lat)
city_location[city] = (long, lat)
city_location
---
{'香港': (114.17, 22.28), '兰州': (103.73, 36.03)}
测试字段证明我们这一段正则生效了,现在可以将内容替换成我们之前写的数据变量:
for line in test_string.split('\n'):
...
city_location
---
{'香港': (114.17, 22.28),
...
'澳门': (113.54, 22.19)}
找出来之后, 就可以求距离了。但是我们需要注意一下,就是城市之间是有一个球面距离,就是在球面同样都是那个纬度,东经60度和东经45度,在北纬的这个位置不一样的时候距离差的是挺大的。最极限的时候在两极是0,最宽的是在赤道上,就会很大。所以有一个专门求经纬度距离的式子,就是经纬度在实际中球面距离的一个式子。
除此之外,还有一些距离公式,比方说余弦距离(Cosine Distance)、欧几里德距离(Euclidean Distance)、曼哈顿距离(Manhattan distance or Manhattan length):
余弦距离
c
o
s
(
p
,
q
)
=
x
×
y
∣
x
∣
×
∣
y
∣
=
∑
i
=
1
n
x
i
y
i
∑
i
=
1
n
x
i
2
∑
i
=
1
n
y
i
2
,
cos(p,q) = \frac{x\times y}{|x|\times|y|} = \frac{\sum_{i=1}^{n}x_iy_i}{\sqrt{\sum_{i=1}^nx_i^2}\sqrt{\sum_{i=1}^ny_i^2}},
cos(p,q)=∣x∣×∣y∣x×y=∑i=1nxi2∑i=1nyi2∑i=1nxiyi,
欧几里德距离
2
维空间中:
d
(
p
,
q
)
=
(
p
1
−
q
1
)
2
+
(
p
2
−
q
2
)
2
n
维空间中
:
d
(
p
,
q
)
=
∑
i
−
1
n
(
p
i
−
q
i
)
2
=
(
p
1
−
q
1
)
2
+
(
p
2
−
q
2
)
2
+
.
.
.
+
(
p
n
−
q
n
)
2
\begin{align*} 2维空间中:& \\ d(p,q) & = \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2} \\ \\ n维空间中: & \\ d(p,q) & = \sqrt{\sum_{i-1}^n(p_i-q_i)^2} \\ & = \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2+...+(p_n - q_n)^2} \end{align*}
2维空间中:d(p,q)n维空间中:d(p,q)=(p1−q1)2+(p2−q2)2=i−1∑n(pi−qi)2=(p1−q1)2+(p2−q2)2+...+(pn−qn)2
曼哈顿距离
d
(
p
,
q
)
=
∣
p
1
−
q
1
∣
+
∣
p
2
−
q
2
∣
\begin{align*} d(p,q) = |p_1-q_1| + |p_2 - q_2| \end{align*}
d(p,q)=∣p1−q1∣+∣p2−q2∣
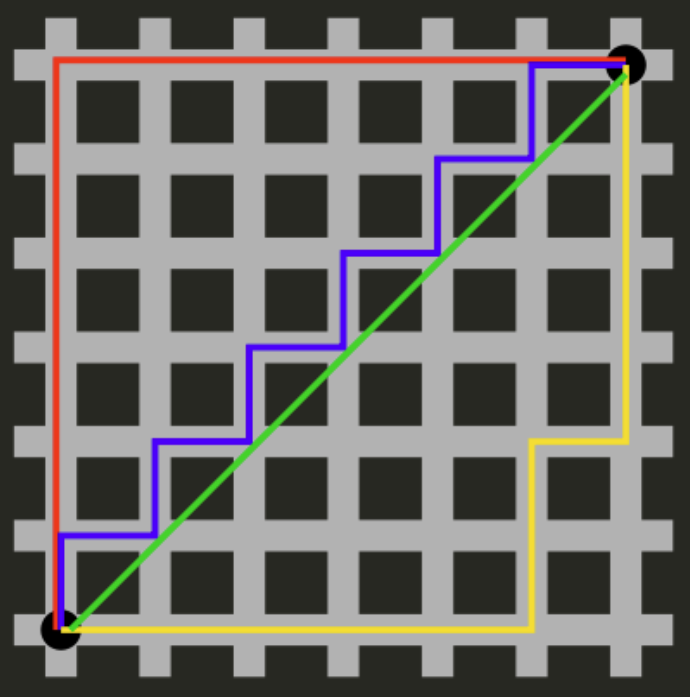
上图中红线代表曼哈顿距离,绿色代表欧氏距离,也就是直线距离,而蓝色和黄色代表等价的曼哈顿距离。曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离。
这些都是不同的求距离的方法。就之前给大家说过,我们可以把对象变成向量,向量要求解距离方法不仅仅只有一种。就像这里,咱们将会使用地理上的球面距离:
import math
def geo_distance(origin, destination):
lon1, lat1 = origin
lon2, lat2 = destination
radius = 6371 # km
dlat = math.radians(lat2 - lat1)
dlon = math.radians(lon2 - lon1)
a = (math.sin(dlat / 2) * math.sin(dlat / 2) +
math.cos(math.radians(lat1)) * math.cos(math.radians(lat2)) *
math.sin(dlon / 2) * math.sin(dlon / 2))
c = 2 * math.atan2(math.sqrt(a), math.sqrt(1 - a))
d = radius * c
return d
这里,咱们涉及到了几个参数,一个是origin, 一个是destination, 我们是要求这两个参数的距离。都是经度、纬度, 类型为tuple of float。然后我们返回一个float。
比如慕尼黑到柏林的例子:
>>> origin = (48.1372, 11.5756) # Munich
>>> destination = (52.5186, 13.4083) # Berlin
>>> round(distance(origin, destination), 1)
504.2
city_location就是每一个城市的位置,我们就可以通过第三方库networkx画出来。
不过这里我们需要注意一点,就是如果是现实中文,我们还需要做一项工作,否则会出现乱码:
# 正常显示中文
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像负号'-'显示为方块的问题
然后我们来将图画出来:
import networkx as nx
%matplotlib inline
city_graph = nx.Graph()
city_graph.add_nodes_from(list(city_location.keys()))
nx.draw(city_graph, city_location, with_labels=True, node_size=30)

看,一个“公鸡”的骨架是不是就出现在图上了?
接下来,咱们就需要实现K-means的部分了。
我们需要将经纬度分别放在x,y里面:
all_x = []
all_y = []
for _, location in city_location.items():
x, y = location
all_x.append(x)
all_y.append(y)
然后我们随机找了k个center:
def get_random_center(all_x, all_y):
r_x = random.uniform(min(all_x), max(all_x))
r_y = random.uniform(min(all_y), max(all_y))
return r_x, r_y
get_random_center(all_x, all_y)
K = 5
centers = {'{}'.format(i+1): get_random_center(all_x, all_y) for i in range(K)}
all_x和all_y是刚刚所有的这些城市的经纬度,让这些城市的经纬度来和每个k去求距离,现在是让所有的x,y去一个一个和k去做对比,找到离它最近的k。
closet_points = defaultdict(list)
for x, y, in zip(all_x, all_y):
closet_c, closet_dis = min([(k, geo_distance((x, y), centers[k])) for k in centers], key=lambda t: t[1])
closet_points[closet_c].append([x, y])
找到了k之后, 我们在所有的图上找到了离k最近的这些点, 然后再求一个means,在离k最近的这些点中求出新的平均值。
def iterate_once(centers, closet_points, threshold=5):
have_changed = False
for c in closet_points:
former_center = centers[c]
neighbors = closet_points[c]
neighbors_center = np.mean(neighbors, axis=0)
if geo_distance(neighbors_center, former_center) > threshold:
centers[c] = neighbors_center
have_changed = True
else:
pass ## keep former center
return centers, have_changed
如果新的中心点和原有的中心点距离大于一个阈值,就把这个central改成新的值,否则就不改变它。
然后不断的去监测它,不断的去根据已知的这个k来求解。离每个k最近的这些点,找到这些最近的点,就求解出来新的means的center,就是平均的center。当我们发现这个center没有改变的时候就停了。
def kmeans(Xs, k, threshold=5):
all_x = Xs[:, 0]
all_y = Xs[:, 1]
K = k
centers = {'{}'.format(i+1): get_random_center(all_x, all_y) for i in range(K)}
changed = True
while changed:
closet_points = defaultdict(list)
for x, y, in zip(all_x, all_y):
closet_c, closet_dis = min([(k, geo_distance((x, y), centers[k])) for k in centers], key=lambda t: t[1])
closet_points[closet_c].append([x, y])
centers, changed = iterate_once(centers, closet_points, threshold)
print('iteration')
return centers
然后我们就可以得出来我们的K-means迭代出来的情况:
kmeans(np.array(list(city_location.values())), k=5, threshold=5)
---
iteration
iteration
iteration
iteration
iteration
iteration
{'1': array([118.14307692, 37.97923077]),
'2': array([115.528, 25.643]),
'3': array([106.22 , 28.16333333]),
'4': array([99.518, 38.86 ]),
'5': array([91.11, 29.97])}
我们可以将这些点画出图来,得到五个能源中心的地点:
plt.scatter(all_x, all_y)
plt.scatter(*zip(*centers.values()))
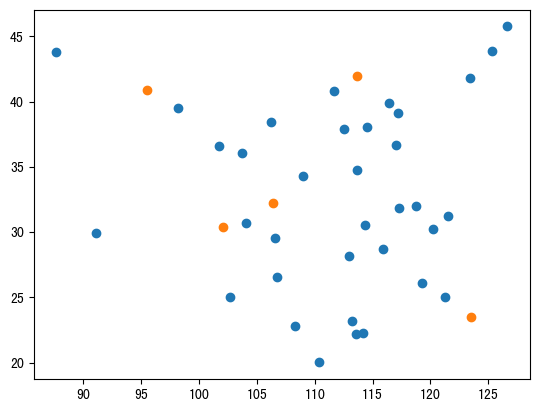
在内蒙有一个, 东南沿海有一个, 重庆有一个,西藏有一个。
感觉咱们这个迭代的次数应该是还不够,如果迭代次数再多一些,能源站应该会放到珠三角这个地方。
这段代码再运行的时间长一点,几个能源中心基本上它会自然而然的变到京津冀江浙沪,还有珠三角和成都重庆这些地方,可能还会有一个在嘉峪关和乌鲁木齐这个地方。
咱们会发现国家的经济中心的形成,其实是有很强的地理关系,非常的神奇。
我们这段代码是咱们从头到尾的把原理实现了一遍, 其实是我们手写的一个K-means。这样的话,大家就对这个原理就了解多了。当你以后要用到它或者要用它一部分的时候才能知道它的用途。
其实K-means也是有一个最大的缺点的,就是最终计算出来的结果会受到初始选取中心的影响。当然,除此之外还有一个缺点,就是它的计算时间复杂度比较高。
尤其是当每次图形越变化越大的时候,就是越斜越细长就会有越受影响,可以设定一个同样的random seed。
这个代码,大家之后一定要自己去敲,去运行。这样就会更加彻底,比绝大多数人更加理解。本节课的相关代码可以去课程仓库中去找,课程的相关问题可以留言提问(不负责免费解答其他无关问题)。
好,那我们机器学习的入门部分,也就随着本节课结束了。下节课开始的很长一段时间之内,咱们可以慢慢的来消化机器学习的相关知识点。