0501 货仓选址 【中位数 距离和的最小值】
描述
在一条数轴上有N家商店，它们的坐标分别为 A[1]~A[N]。现在需要在数轴上建立一家货仓，每天清晨，从货仓到每家商店都要运送一车商品。为了提高效率，求把货仓建在何处，可以使得货仓到每家商店的距离之和最小。
输入格式
第一行一个整数N，第二行N个整数A[1]~A[N]。
输出格式
一个整数，表示距离之和的最小值。
样例输入
4
6 2 9 1
样例输出
12
数据范围与约定
对于100%的数据: N<=100000, A[i]<=1000000
Contest Hunter - 信息学自助比赛平台

问题：x=？，求|A1-x|+ |A2-x|+…+|An-x|最小值。
思路：将A[0]~A[N-1]排序，设货仓建在x坐标处，x 的左侧商店有 P 家，右侧Q 家，若P<Q，则把货仓向右移动移动 1 单位距离，则总距离和就会减少Q-P，同理，若P>Q，则货仓向左移动时总距离和变小，当 P=Q 时为最优解。

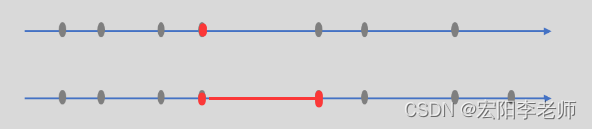
因此，货仓应该建在中位数处，当N为奇数时，建在A[N/2]处；当 N为偶数时，建在A[（N-1）/2]~A[N/2]之间（包括端点）的任何位置都是。

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,a[N],m;
int main()
{	
	cin>>n;
	for(int i=0;i<n;i++)cin>>a[i];
	sort(a,a+n);
	int ans=0;
	m=a[n/2];
	for(int i=0;i<n;i++)
		ans+=abs(m-a[i]);
	cout<<ans<<endl;
    return 0;
}