算法实现基本与高斯消元法求解线性方程组相同，同样还是三层循环进行消元和回代，只是增广矩阵的规模由n×n+1变成了n×2n，因此算法复杂度仍然为O(n3)。

A=[1,1,2,1;1,2,0,1;1,4,2,1;1,8,2,4];
b=eye(4);
A_b=[A,b];
[n,m]=size(A_b);
for i=1:n
    for j=m:-1:i
        A_b(i,j)=A_b(i,j)/A_b(i,i);
    end
    for j=i+1:n
        for k=m:-1:i
            A_b(j,k)=A_b(j,k)-A_b(j,i)*A_b(i,k);
        end
    end
%     fprintf('第%d次消元\n',i);
%     disp(rats(A_b));
end
for i=n-1:-1:1
    for j=i:-1:1
        for k=m:-1:n+1
            A_b(j,k)=A_b(j,k)-A_b(j,i+1)*A_b(i+1,k);
        end
        A_b(j,i+1)=0;
    end
%     fprintf('第%d次回代\n',n-i);
%     disp(rats(A_b));
end
gaussInverse=A_b(:,end-3:end);
fprintf('高斯消元求逆\n');
disp(rats(gaussInverse));
matlabInverse=A^(-1);
fprintf('matlab内置函数求逆\n');
disp(rats(matlabInverse));
difference=gaussInverse-matlabInverse;
figure(1);
heatmap(difference);  % 绘制热力图
colorbar;    % 添加颜色条
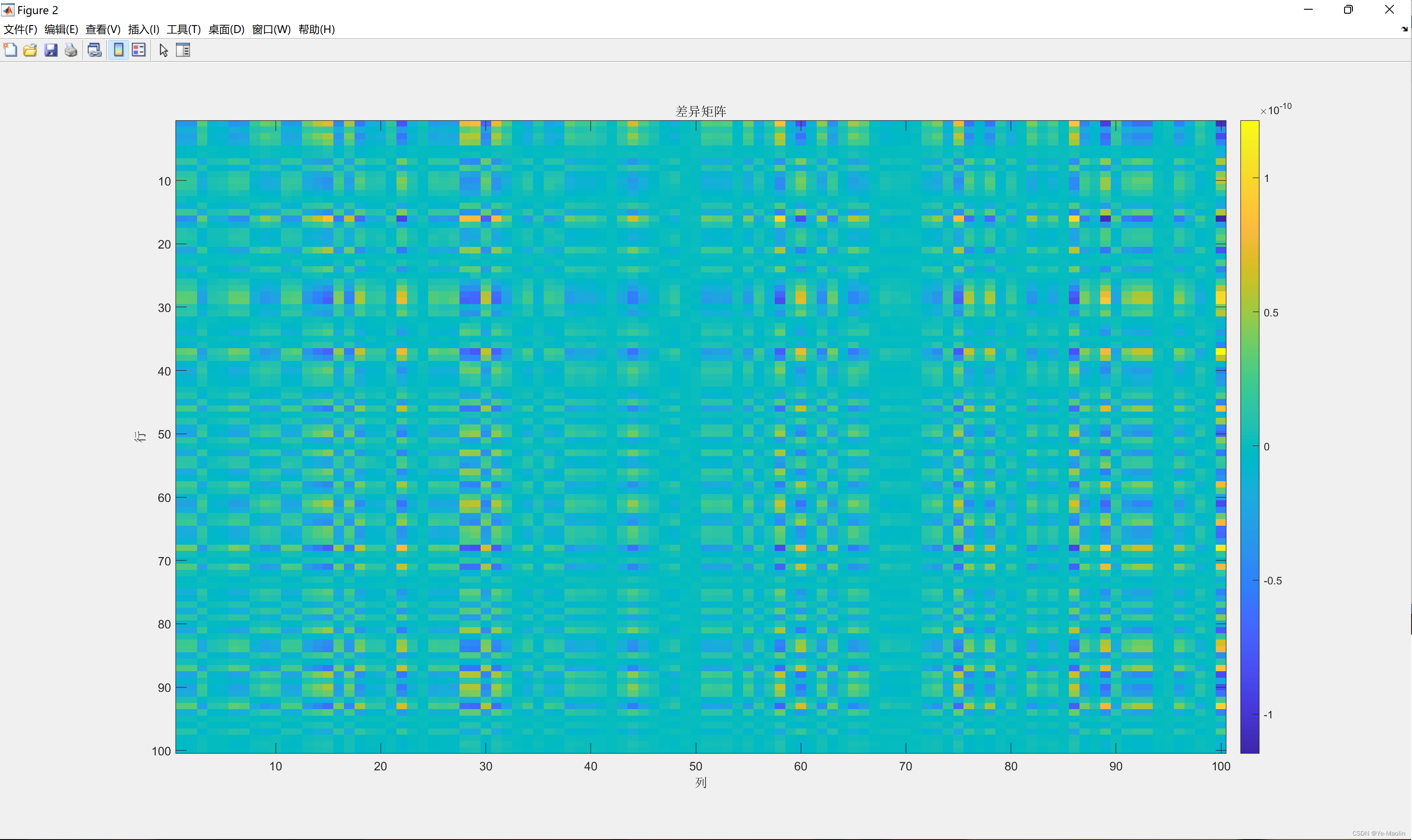
title('差异矩阵');  % 添加标题
xlabel('列');  % 添加 x 轴标签
ylabel('行');  % 添加 y 轴标签
figure(2);
imagesc(difference);  % 绘制差异矩阵
colorbar;   % 添加颜色条
title('差异矩阵');  % 添加标题
xlabel('列');  % 添加 x 轴标签
ylabel('行');  % 添加 y 轴标签

与matlab内置求逆效果对比